Given the root of a complete binary tree, return the number of the nodes in the tree.
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Design an algorithm that runs in less than O(n) time complexity.
Example 1:

Input: root = [1,2,3,4,5,6] Output: 6
Example 2:
Input: root = [] Output: 0
Example 3:
Input: root = [1] Output: 1
Constraints:
- The number of nodes in the tree is in the range
[0, 5 * 104]. 0 <= Node.val <= 5 * 104- The tree is guaranteed to be complete.
Solution: Recursion
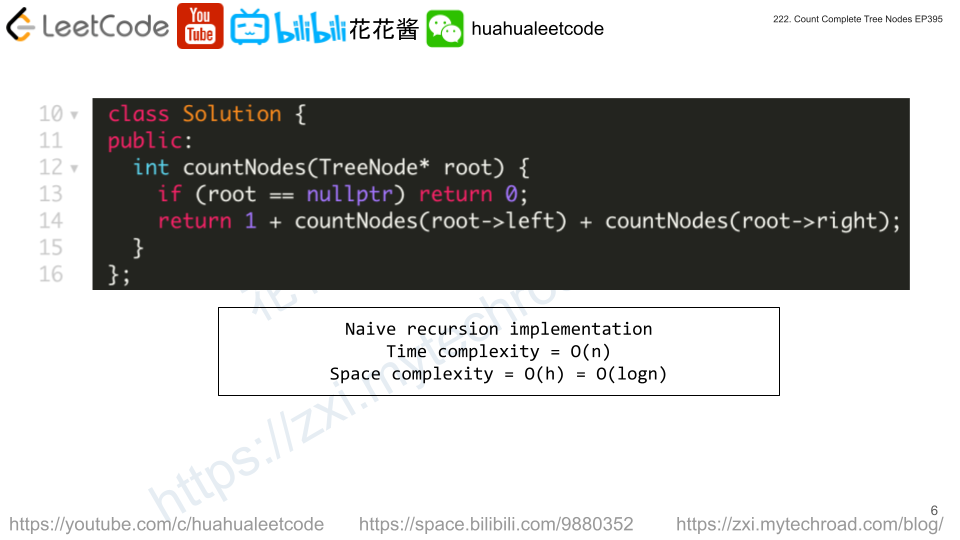
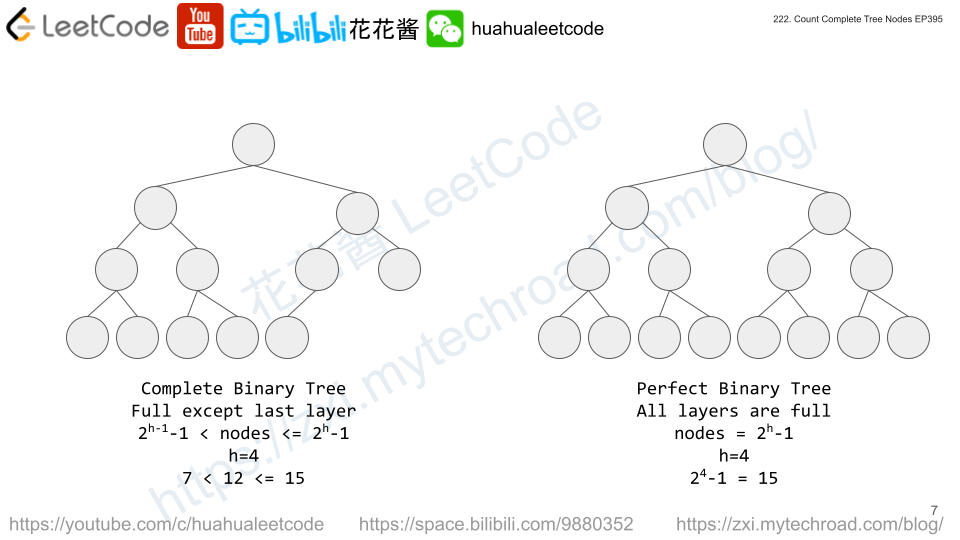


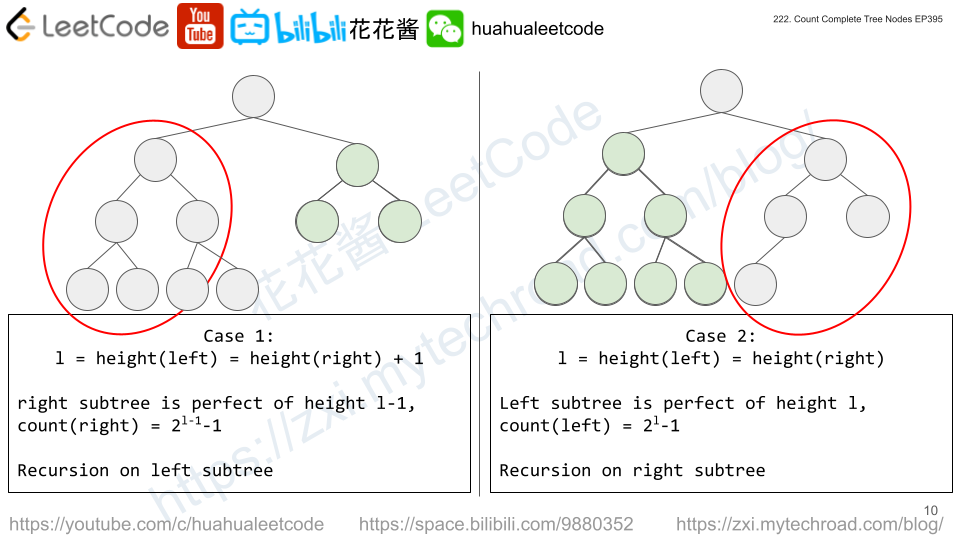
For each node, count the height of it’s left and right subtree by going left only.
Let L = height(left) R = height(root), if L == R, which means the left subtree is perfect.
It has (2^L – 1) nodes, +1 root, we only need to count nodes of right subtree recursively.
If L != R, L must be R + 1 since the tree is complete, which means the right subtree is perfect.
It has (2^(L-1) – 1) nodes, +1 root, we only need to count nodes of left subtree recursively.
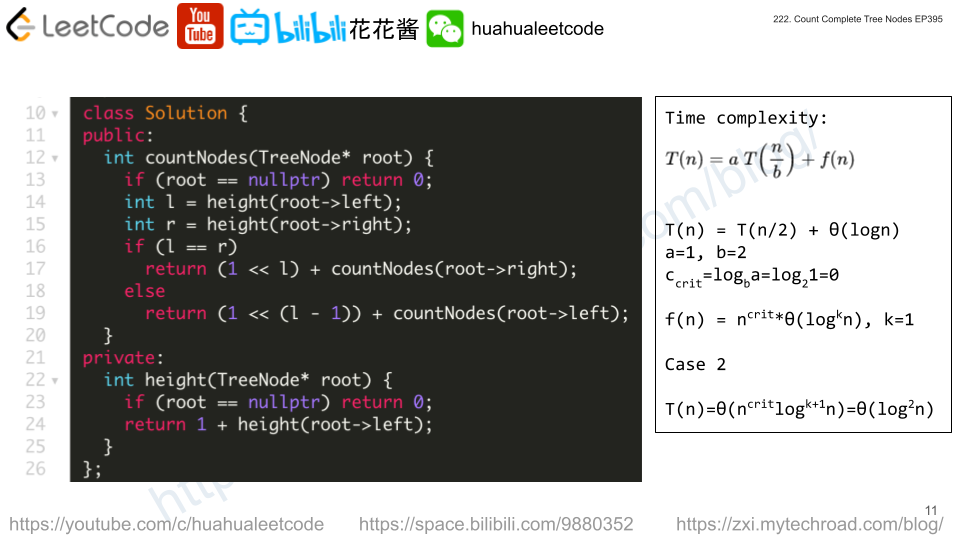
Time complexity: T(n) = T(n/2) + O(logn) = O(logn*logn)
Space complexity: O(logn)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// Author: Huahua class Solution { public: int countNodes(TreeNode* root) { if (root == nullptr) return 0; int l = depth(root->left); int r = depth(root->right); if (l == r) return (1 << l) + countNodes(root->right); else return (1 << (l - 1)) + countNodes(root->left); } private: int depth(TreeNode* root) { if (root == nullptr) return 0; return 1 + depth(root->left); } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment