Posts published in February 2018

花花酱 Time/Space Complexity of Recursion Functions SP4

By zxi on February 7, 2018

How to analyze the time and space complexity of a recursion function?

如何分析一个递归函数的时间/空间复杂度？

We can answer that using master theorem or induction in most of the cases.

在大部分时候我们可以使用主方法和数学归纳法来进行解答。

First of all, we need to write down the recursion relation of a function.

首先我们要写出一个函数的递归表达式。

def func(n):

if n < 0: return 1

return func(n/2) + func(n/2)

Let’s use T(n) to denote the running time of func with input size of n.

让我们用T(n)来表示func函数在输入规模为n的运行时间。

Then we have：

那么我们有：

T(n) = 2*T(n/2) + O(1)

a = 2, b = 2, c_crit = logb(a) = 1, f(n) = n^c, c = 0.

c < c_crit, apply master theorem case 1:

根据主方法第一条我们得到

T(n) = Θ(n^c_crit) = Θ(n)

Let’s look at another example:

def func(n):

if n < 0: return 1

s = 0

for i in range(n):

s += i

return s + func(n/2) + func(n/2)

T(n) = 2*T(n/2) + O(n)

a = 2, b = 2, c_crit = logb(a) = 1, f(n) = n^c, c = 1,

c = c_crit, apply master theorem case 2:

根据主方法第二条我们得到

T(n) =Θ(n^c_crit * (logn)^1)) = Θ(nlogn)

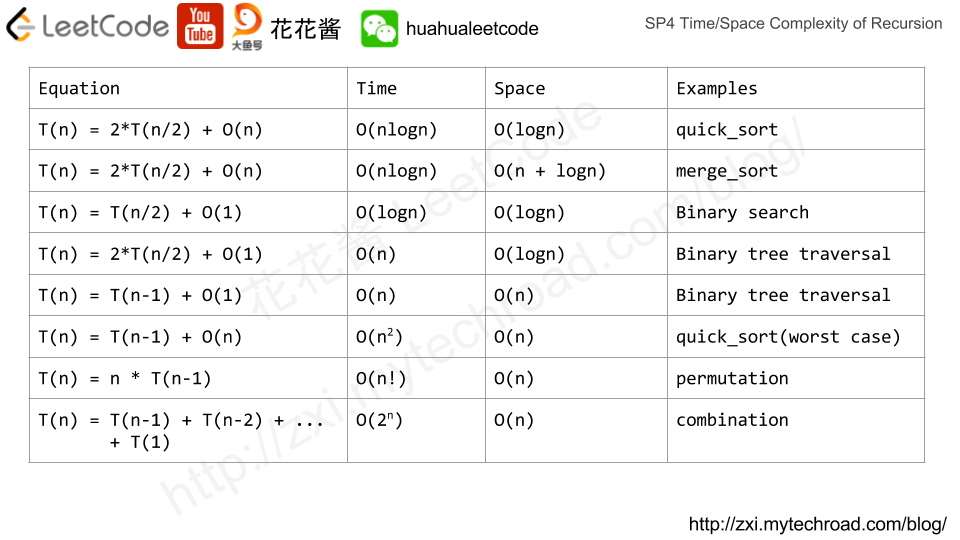
Cheatsheet

Equation	Time	Space	Examples
T(n) = 2*T(n/2) + O(n)	O(nlogn)	O(logn)	quick_sort
T(n) = 2*T(n/2) + O(n)	O(nlogn)	O(n + logn)	merge_sort
T(n) = T(n/2) + O(1)	O(logn)	O(logn)	Binary search
T(n) = 2*T(n/2) + O(1)	O(n)	O(logn)	Binary tree traversal
T(n) = T(n-1) + O(1)	O(n)	O(n)	Binary tree traversal
T(n) = T(n-1) + O(n)	O(n^2)	O(n)	quick_sort(worst case)
T(n) = n * T(n-1)	O(n!)	O(n)	permutation
T(n) = T(n-1)+T(n-2)+…+T(1)	O(2^n)	O(n)	combination

For recursion with memorization:

Time complexity: |# of subproblems| * |exclusive running time of a subproblem|

Example 1:

def fib(n):

if n < 1: return 1

if m[n]: return m[n]

m[n] = fib(n - 1) + fib(n - 2)

return m[n]

To solve fib(n), there are n subproblems fib(0), fib(1), …, fib(n)

each sub problem takes O(1) to solve

Time complexity: O(n)

Space complexity: O(n) + O(n) * O(1) = O(n)

Example 2:

LC 741 Cherry Pickup

dp(x1, y1, x2):

if min(x1, y1, x2) < 0: return 0

if m[x1][y1][x2]: return m[x1][y1][x2]

ans = max(dp(x1 - 1, y1, x2 - 1),

dp(x1, y1 - 1, x2),

dp(x1, y1 - 1, x2 - 1),

dp(x1 - 1, y1, x2))

m[x1][y1][x2] = ans

return m[x1][y1][x2]

To solve dp(n, n, n), there are n^3 subproblems

each subproblem takes O(1) to solve

Max recursion depth O(n)

Time complexity: O(n^3) * O(1) = O(n^3)

Space complexity: O(n^3) + O(n) * O(1) = O(n^3)

Example 3:

LC 312: Burst Balloon

dp(i, j):

if m[i][j]: return m[i][j]

for k in range(i, j + 1):

ans = max(ans, dp(i, k - 1) + C + dp(k + 1, j))

m[i][j] = ans

return m[i][j]

To solve dp(0, n), there are n^2 subproblems dp(0, 0), dp(0, 1), …, dp(n-1, n)

each subproblem takes O(n) to solve

Max recursion depth O(n)

Time complexity: O(n^2) * O(n) = O(n^3)

Space complexity: O(n^2) + O(n) * O(1) = O(n^2)

Slides:

花花酱 LeetCode 773. Sliding Puzzle

By zxi on February 6, 2018

题目大意：给你一个2×3的棋盘，放着0-5。每一步0可以和上下左右的一个数交换。问需要多少步可以构成123450的棋盘状态。

Problem:

On a 2×3 board, there are 5 tiles represented by the integers 1 through 5, and an empty square represented by 0.

A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given a puzzle board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

Examples:

Input: board = [[1,2,3],[4,0,5]]

Output: 1

Explanation: Swap the 0 and the 5 in one move.

Input: board = [[1,2,3],[5,4,0]]

Output: -1

Explanation: No number of moves will make the board solved.

Input: board = [[4,1,2],[5,0,3]]

Output: 5

Explanation: 5 is the smallest number of moves that solves the board.

An example path:

After move 0: [[4,1,2],[5,0,3]]

After move 1: [[4,1,2],[0,5,3]]

After move 2: [[0,1,2],[4,5,3]]

After move 3: [[1,0,2],[4,5,3]]

After move 4: [[1,2,0],[4,5,3]]

After move 5: [[1,2,3],[4,5,0]]

1 2	Input: board = [[3,2,4],[1,5,0]] Output: 14

Solution: BFS

Time complexity: O(6!)

Space complexity: O(6!)

C++

// Author: Huahua

// Running time: 9 ms

class Solution {

public:

int slidingPuzzle(vector<vector<int>>& board) {

constexpr int kRows = 2;

constexpr int kCols = 3;

string goal;

string start;

for (int i = 0; i < board.size(); ++i)

for (int j = 0; j < board[0].size(); ++j) {

start += (board[i][j] + '0');

goal += (i * kCols + j + 1) % (kRows * kCols) + '0'; // 12345...0

}

if (start == goal) return 0;

constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};

set<string> visited{start};

int steps = 0;

queue<string> q;

q.push(start);

while (!q.empty()) {

++steps;

int size = q.size();

while (size-- > 0) {

string s = q.front();

q.pop();

int p = s.find('0');

int y = p / kCols;

int x = p % kCols;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i][0];

int ty = y + dirs[i][1];

if (tx < 0 || ty < 0 || tx >= kCols || ty >= kRows) continue;

int pp = ty * kCols + tx;

string t(s);

swap(t[p], t[pp]);

if (visited.count(t)) continue;

if (t == goal) return steps;

visited.insert(t);

q.push(t);

}

return -1;

}

};

Simplified, only works on 3×2 board

// Author: Huahua

// Running time: 9 ms

class Solution {

public:

int slidingPuzzle(vector<vector<int>>& board) {

const string goal = "123450";

string start;

for (int i = 0; i < board.size(); ++i)

for (int j = 0; j < board[0].size(); ++j)

start += (board[i][j] + '0');

if (start == goal) return 0;

const vector<vector<int>> idx{{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};

set<string> visited{start};

int steps = 0;

queue<pair<string, int>> q;

q.emplace(start, start.find('0'));

while (!q.empty()) {

++steps;

int size = q.size();

while (size-- > 0) {

const auto& p = q.front();

q.pop();

for (int index : idx[p.second]) {

string t(p.first);

swap(t[p.second], t[index]);

if (visited.count(t)) continue;

if (t == goal) return steps;

visited.insert(t);

q.emplace(t, index);

}

return -1;

}

};

花花酱 LeetCode 636. Exclusive Time of Functions

By zxi on February 5, 2018

题目大意：给你一些函数的起始/终止时间的日志，让你输出每个函数的总运行时间。假设单核单线程，支持递归函数。

Given the running logs of n functions that are executed in a nonpreemptive single threaded CPU, find the exclusive time of these functions.

Each function has a unique id, start from 0 to n-1. A function may be called recursively or by another function.

A log is a string has this format : function_id:start_or_end:timestamp. For example, "0:start:0" means function 0 starts from the very beginning of time 0. "0:end:0" means function 0 ends to the very end of time 0.

Exclusive time of a function is defined as the time spent within this function, the time spent by calling other functions should not be considered as this function’s exclusive time. You should return the exclusive time of each function sorted by their function id.

Example 1:

Input:

n = 2

logs =

["0:start:0",

"1:start:2",

"1:end:5",

"0:end:6"]

Output:[3, 4]

Explanation:

Function 0 starts at time 0, then it executes 2 units of time and reaches the end of time 1.

Now function 0 calls function 1, function 1 starts at time 2, executes 4 units of time and end at time 5.

Function 0 is running again at time 6, and also end at the time 6, thus executes 1 unit of time.

So function 0 totally execute 2 + 1 = 3 units of time, and function 1 totally execute 4 units of time.

Note:

Input logs will be sorted by timestamp, NOT log id.
Your output should be sorted by function id, which means the 0th element of your output corresponds to the exclusive time of function 0.
Two functions won’t start or end at the same time.
Functions could be called recursively, and will always end.
1 <= n <= 100

Solution: Simulate using stack

// Author: Huahua

// Running time: 35 ms

class Solution {

public:

vector<int> exclusiveTime(int n, vector<string>& logs) {

vector<int> ans(n, 0);

char action[6];

int fid;

int curr;

int prev;

stack<int> s;

for (const string& log : logs) {

sscanf(log.c_str(), "%d:%[a-z]:%d", &fid, action, &curr);

if (action[0] == 's') {

if (!s.empty())

ans[s.top()] += curr - prev;

s.push(fid);

prev = curr;

} else {

ans[s.top()] += curr - prev + 1;

s.pop();

prev = curr + 1;

}

return ans;

}

};

花花酱 LeetCode 464. Can I Win

By zxi on February 4, 2018

题目大意：两个人从1到M中每次取出一个数加到当前的总和上，第一个达到或超过T的人获胜。问你第一个玩家能不能获胜。

In the “100 game,” two players take turns adding, to a running total, any integer from 1..10. The player who first causes the running total to reach or exceed 100 wins.

What if we change the game so that players cannot re-use integers?

For example, two players might take turns drawing from a common pool of numbers of 1..15 without replacement until they reach a total >= 100.

Given an integer maxChoosableInteger and another integer desiredTotal, determine if the first player to move can force a win, assuming both players play optimally.

You can always assume that maxChoosableInteger will not be larger than 20 and desiredTotal will not be larger than 300.

Example

Input:

maxChoosableInteger = 10

desiredTotal = 11

Output:

false

Explanation:

No matter which integer the first player choose, the first player will lose.

The first player can choose an integer from 1 up to 10.

If the first player choose 1, the second player can only choose integers from 2 up to 10.

The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.

Same with other integers chosen by the first player, the second player will always win.

Solution: Recursion with memoization

Time complexity: O(2^M)

Space complexity: O(2^M)

C++

// Author: Huahua

// Running time: 19 ms (<98.70%)

class Solution {

public:

bool canIWin(int M, int T) {

const int sum = M * (M + 1) / 2;

if (sum < T) return false;

if (T <= 0) return true;

m_ = vector<char>(1 << M, 0);

return canIWin(M, T, 0);

}

private:

vector<char> m_; // 0: unknown, 1: won, -1: lost

bool canIWin(int M, int T, int state) {

if (T <= 0) return false;

if (m_[state]) return m_[state] == 1;

for (int i = 0; i < M; ++i) {

if (state & (1 << i)) continue; // number i used

// The next player can not win, current player wins

if (!canIWin(M, T - (i + 1), state | (1 << i)))

return m_[state] = 1;

}

// Current player loses.

m_[state] = -1;

return false;

}

};

Java

// Author: Huahua

// Running time: 20 ms

class Solution {

private byte[] m_;

public boolean canIWin(int M, int T) {

int sum = M * (M + 1) / 2;

if (sum < T) return false;

if (T <= 0) return true;

m_ = new byte[1 << M];

return canIWin(M, T, 0);

}

private boolean canIWin(int M, int T, int state) {

if (T <= 0) return false;

if (m_[state] != 0) return m_[state] == 1;

for (int i = 0; i < M; ++i) {

if ((state & (1 << i)) > 0) continue;

if (!canIWin(M, T - (i + 1), state | (1 << i))) {

m_[state] = 1;

return true;

}

m_[state] = -1;

return false;

}

Python3

"""

Author: Huahua

Running time: 706 ms

"""

class Solution:

def canIWin(self, M, T):

def win(M, T, m, state):

if T <= 0: return False

if m[state] != 0: return m[state] == 1

for i in range(M):

if (state & (1 << i)) > 0: continue

if not win(M, T - i - 1, m, state | (1 << i)):

m[state] = 1

return True

m[state] = -1

return False

s = M * (M + 1) / 2

if s < T: return False

if T <= 0: return True

if s == T: return (M % 2) == 1

m = [0] * (1 << M)

return win(M, T, m, 0)

花花酱 LeetCode 768. Max Chunks To Make Sorted II

By zxi on February 2, 2018

题目大意：给你一堆数让你分块，每块独立排序后和整个数组排序的结果相同，问你最多能分为几块。

Problem:

This question is the same as “Max Chunks to Make Sorted” except the integers of the given array are not necessarily distinct, the input array could be up to length 2000, and the elements could be up to 10**8.

Given an array arr of integers (not necessarily distinct), we split the array into some number of “chunks” (partitions), and individually sort each chunk. After concatenating them, the result equals the sorted array.

What is the most number of chunks we could have made?

Example 1:

Input: arr = [5,4,3,2,1]

Output: 1

Explanation:

Splitting into two or more chunks will not return the required result.

For example, splitting into [5, 4], [3, 2, 1] will result in [4, 5, 1, 2, 3], which isn't sorted.

Example 2:

Input: arr = [2,1,3,4,4]

Output: 4

Explanation:

We can split into two chunks, such as [2, 1], [3, 4, 4].

However, splitting into [2, 1], [3], [4], [4] is the highest number of chunks possible.

Note:

arr will have length in range [1, 2000].
arr[i] will be an integer in range [0, 10**8].

Idea:

Reduce the problem to 花花酱 769. Max Chunks To Make Sorted by creating a mapping from number to index in the sorted array.

arr = [2, 3, 5, 4, 4]

sorted = [2, 3, 4, 4, 5]

indices = [0, 1, 4, 2, 3]

Solution: Mapping

Time complexity: O(nlogn)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 19 ms

class Solution {

public:

int maxChunksToSorted(vector<int>& arr) {

vector<int> v(arr.size());

std::iota(v.begin(), v.end(), 0);

std::sort(v.begin(), v.end(), [&arr](const int i1, const int i2){

return arr[i1] == arr[i2] ? (i1 < i2) : arr[i1] < arr[i2];

});

int ans = 0;

int m = 0;

for (int i = 0; i < v.size(); ++i) {

m = max(m, v[i]);

if (m == i) ++ans;

}

return ans;

}

};

Python3

"""

Author: Huahua

Running time: 95 ms

"""

class Solution:

def maxChunksToSorted(self, arr):

v = sorted([(n << 32) | i for i, n in enumerate(arr)])

m = 0

ans = 0

for i, n in enumerate(v):

m = max(m, n & 0xffffffff)

if i == m: ans += 1

return ans