In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0) and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).
In one move the snake can:
- Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
- Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
- Rotate clockwise if it’s in a horizontal position and the two cells under it are both empty. In that case the snake moves from
(r, c)and(r, c+1)to(r, c)and(r+1, c). - Rotate counterclockwise if it’s in a vertical position and the two cells to its right are both empty. In that case the snake moves from
(r, c)and(r+1, c)to(r, c)and(r, c+1).
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return -1.
Example 1:
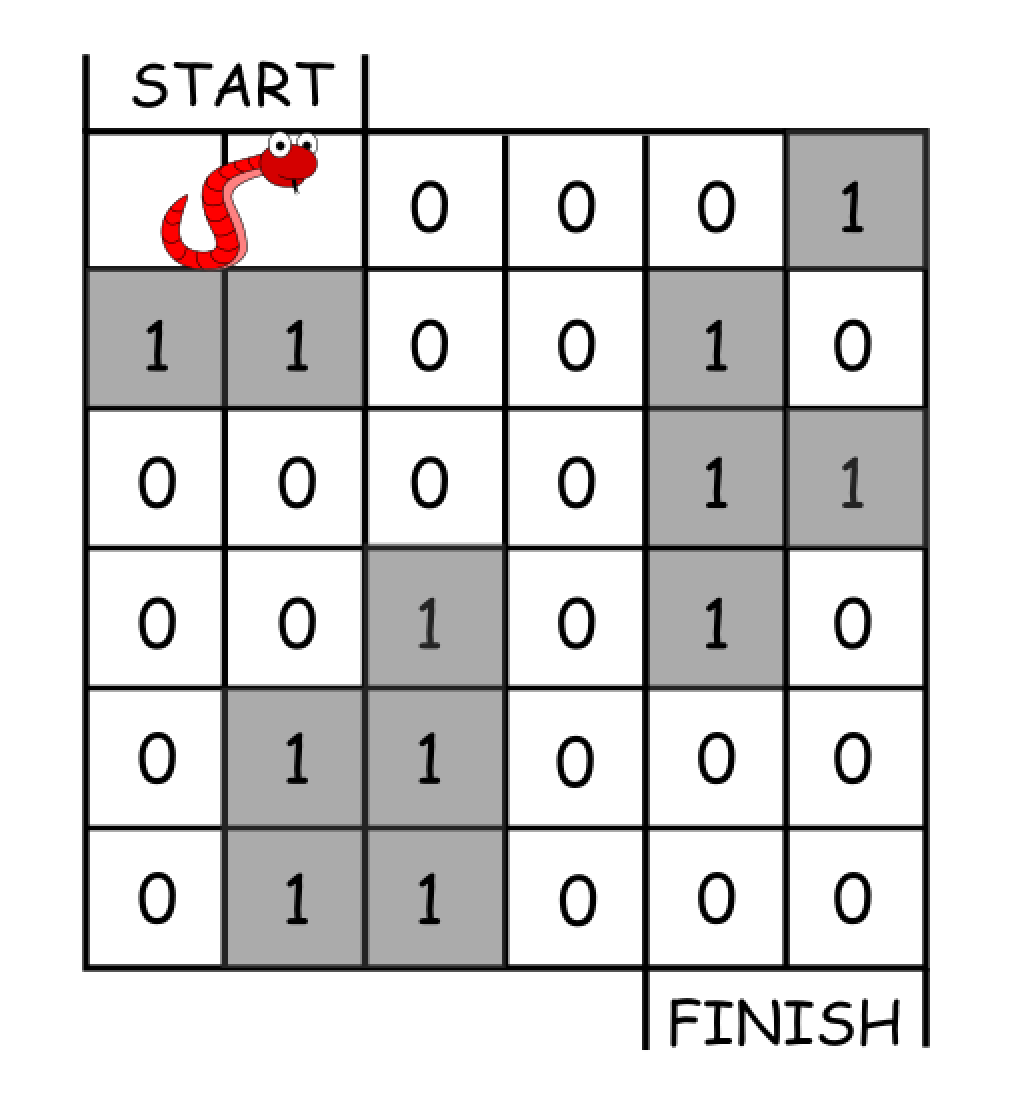
Input: grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
Output: 11
Explanation:
One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].
Example 2:
Input: grid = [[0,0,1,1,1,1], [0,0,0,0,1,1], [1,1,0,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,0]] Output: 9
Constraints:
2 <= n <= 1000 <= grid[i][j] <= 1- It is guaranteed that the snake starts at empty cells.
Solution1: BFS
Time complexity: O(n^2)
Space complexity: O(n^2)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
// Author: Huahua, 48 ms, 18.1 MB class Solution { public: inline int pos(int x, int y) { return y * 100 + x; } inline int encode(int p1, int p2) { return (p1 << 16) | p2; } int minimumMoves(vector<vector<int>>& grid) { int n = grid.size(); queue<pair<int, int>> q; unordered_set<int> seen; q.push({pos(0, 0), pos(1, 0)}); // tail, head seen.insert(encode(pos(0, 0), pos(1, 0))); int steps = 0; auto valid = [&](int x, int y) { bool v = x >= 0 && x < n && y >= 0 && y < n && !grid[y][x]; return v; }; while (!q.empty()) { int size = q.size(); while (size--) { auto p = q.front(); q.pop(); int y0 = p.first / 100; int x0 = p.first % 100; int y1 = p.second / 100; int x1 = p.second % 100; if (x0 == n - 2 && y0 == n - 1 && x1 == n - 1 && y1 == n - 1) { return steps; } bool h = y0 == y1; for (int i = 0; i < 3; ++i) { int tx0 = x0; int ty0 = y0; int tx1 = x1; int ty1 = y1; int rx = x0; int ry = y0; switch (i) { case 0: // down ++ty0; ++ty1; break; case 1: // right ++tx0; ++tx1; break; case 2: // rotate ++rx; ++ry; if (h) { // clockwise --tx1; ++ty1; } else { // counterclockwise ++tx1; --ty1; } break; } if (!valid(tx0, ty0) || !valid(tx1, ty1) || !valid(rx, ry)) continue; int key = encode(pos(tx0, ty0), pos(tx1, ty1)); if (seen.count(key)) continue; seen.insert(key); q.push({pos(tx0, ty0), pos(tx1, ty1)}); } } ++steps; } return -1; } }; |
Solution 2: DP
dp[i][j].first = min steps to reach i,j (tail pos) facing right
dp[i][j].second = min steps to reach i, j (tail pos) facing down
ans = dp[n][n-1].first
Time complexity: O(n^2)
Space complexity: O(n^2)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// Author: Huahua, 16 ms, 12.1MB class Solution { public: int minimumMoves(vector<vector<int>>& grid) { constexpr int kInf = 1e9; const int n = grid.size(); vector<vector<pair<int, int>>> dp(n + 1, vector<pair<int, int>>(n + 1, {kInf, kInf})); dp[0][1].first = dp[1][0].first = -1; for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) { bool h = false; bool v = false; if (!grid[i - 1][j - 1] && j < n && !grid[i - 1][j]) { dp[i][j].first = min(dp[i - 1][j].first, dp[i][j - 1].first) + 1; h = true; } if (!grid[i - 1][j - 1] && i < n && !grid[i][j - 1]) { dp[i][j].second = min(dp[i - 1][j].second, dp[i][j - 1].second) + 1; v = true; } if (v && j < n && !grid[i][j]) dp[i][j].second = min(dp[i][j].second, dp[i][j].first + 1); if (h && i < n && !grid[i][j]) dp[i][j].first = min(dp[i][j].first, dp[i][j].second + 1); } return dp[n][n - 1].first >= kInf ? -1 : dp[n][n - 1].first; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment