Problem:
Design and implement a data structure for Least Frequently Used (LFU) cache. It should support the following operations: get and put.
get(key) – Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.
put(key, value) – Set or insert the value if the key is not already present. When the cache reaches its capacity, it should invalidate the least frequently used item before inserting a new item. For the purpose of this problem, when there is a tie (i.e., two or more keys that have the same frequency), the least recently used key would be evicted.
Follow up:
Could you do both operations in O(1) time complexity?
Example:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
LFUCache cache = new LFUCache( 2 /* capacity */ ); cache.put(1, 1); cache.put(2, 2); cache.get(1); // returns 1 cache.put(3, 3); // evicts key 2 cache.get(2); // returns -1 (not found) cache.get(3); // returns 3. cache.put(4, 4); // evicts key 1. cache.get(1); // returns -1 (not found) cache.get(3); // returns 3 cache.get(4); // returns 4 |
Idea:
Hashtable + balanced search tree
Hashtable + double linked list
Solution 1: O(logc) c is the capacity
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
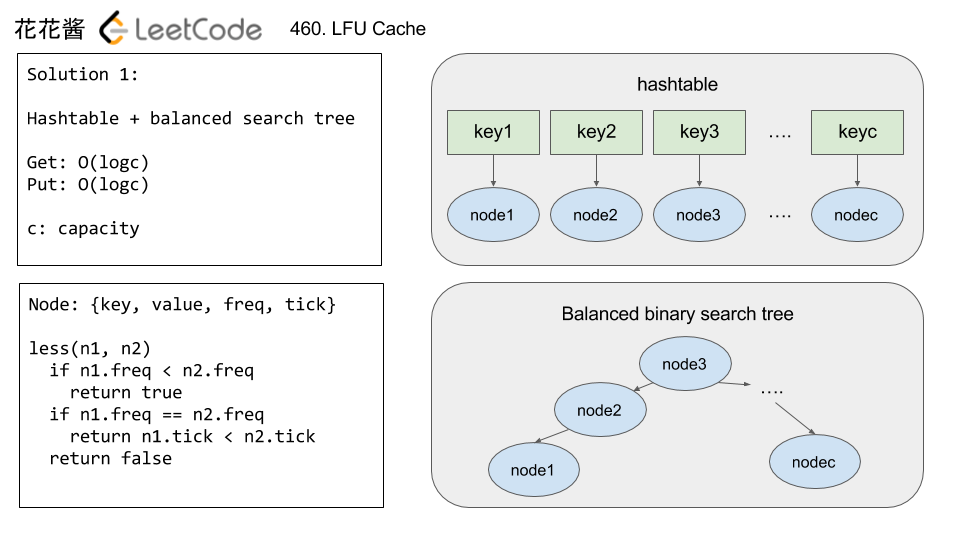
// Author: Huahua // Running time: 99 ms struct CacheNode { int key; int value; int freq; long tick; // Defines the order, smaller one will be evicted first bool operator <(const CacheNode& rhs) const { if (freq < rhs.freq) return true; if (freq == rhs.freq) return tick < rhs.tick; return false; } }; class LFUCache { public: LFUCache(int capacity):capacity_(capacity), tick_(0) {} int get(int key) { auto it = m_.find(key); if (it == m_.cend()) return -1; int value = it->second.value; touch(it->second); return value; } void put(int key, int value) { if (capacity_ == 0) return; auto it = m_.find(key); if (it != m_.cend()) { // Key exists, update value and touch it->second.value = value; touch(it->second); return; } if (m_.size() == capacity_) { // Remove the first node in cache const CacheNode& node = *cache_.cbegin(); m_.erase(node.key); cache_.erase(node); } CacheNode node{key, value, 1, ++tick_}; m_[node.key] = node; cache_.insert(node); } private: void touch(CacheNode& node) { cache_.erase(node); // log(capacity) ++node.freq; node.tick = ++tick_; cache_.insert(node); // log(capacity) } long tick_; int capacity_; unordered_map<int, CacheNode> m_; set<CacheNode> cache_; }; |
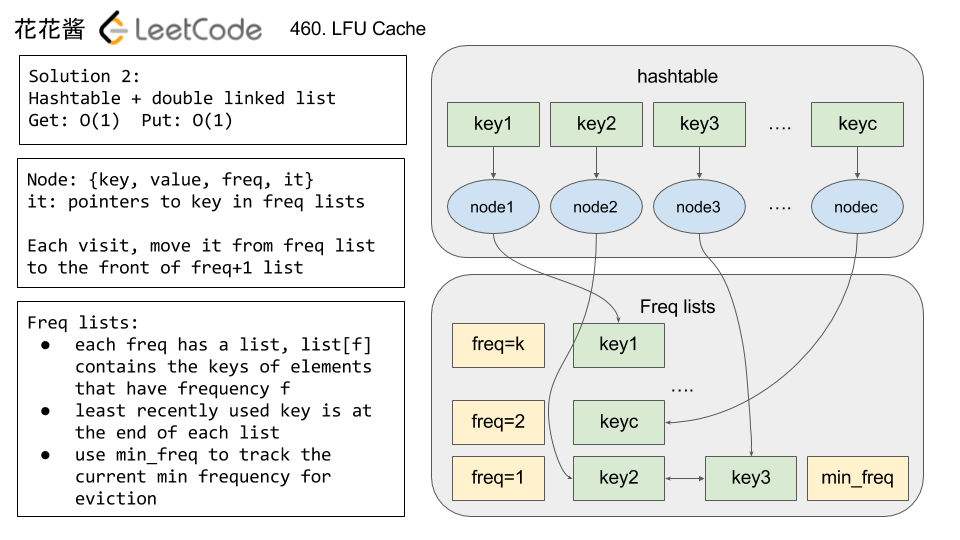
Solution 2: O(1)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
// Author: Huahua // Running time: 89 ms (beats 96.3%) struct CacheNode { int key; int value; int freq; // pointer to the node in the list list<int>::const_iterator it; }; class LFUCache { public: LFUCache(int capacity): capacity_(capacity), min_freq_(0) {} int get(int key) { auto it = n_.find(key); if (it == n_.cend()) return -1; touch(it->second); return it->second.value; } void put(int key, int value) { if (capacity_ == 0) return; auto it = n_.find(key); if (it != n_.cend()) { // Key already exists, update the value and touch it it->second.value = value; touch(it->second); return; } if (n_.size() == capacity_) { // No capacity, need to remove one entry that // 1. has the lowest freq // 2. least recently used if there are multiple ones // Step 1: remove the element from min_freq_ list const int key_to_evict = l_[min_freq_].back(); l_[min_freq_].pop_back(); // Step 2: remove the key from cache n_.erase(key_to_evict); } // We know new item has freq of 1, thus set min_freq to 1 const int freq = 1; min_freq_ = freq; // Add the key to the freq list l_[freq].push_front(key); // Create a new node n_[key] = {key, value, freq, l_[freq].cbegin()}; } private: void touch(CacheNode& node) { // Step 1: update the frequency const int prev_freq = node.freq; const int freq = ++(node.freq); // Step 2: remove the entry from old freq list l_[prev_freq].erase(node.it); if (l_[prev_freq].empty() && prev_freq == min_freq_) { // Delete the list l_.erase(prev_freq); // Increase the min freq ++min_freq_; } // Step 4: insert the key into the front of the new freq list l_[freq].push_front(node.key); // Step 5: update the pointer node.it = l_[freq].cbegin(); } int capacity_; int min_freq_; // key -> CacheNode unordered_map<int, CacheNode> n_; // freq -> keys with freq unordered_map<int, list<int>> l_; }; |
