Posts published in “Data Structure”

花花酱 LeetCode 208. Implement Trie (Prefix Tree)

By zxi on September 27, 2017

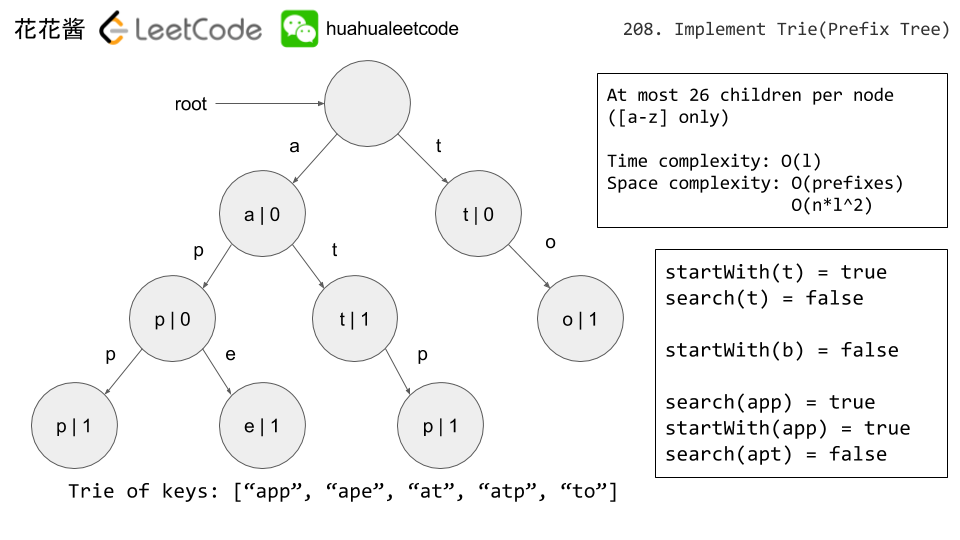
Problem:

Implement a trie with insert, search, and startsWith methods.

Note:
You may assume that all inputs are consist of lowercase letters a-z.

Idea:

Tree/children array

Solution:

C++ / Array

// Author: Huahua

// Running time: 99 ms

class Trie {

public:

/** Initialize your data structure here. */

Trie(): root_(new TrieNode()) {}

/** Inserts a word into the trie. */

void insert(const string& word) {

TrieNode* p = root_.get();

for (const char c : word) {

if (!p->children[c - 'a'])

p->children[c - 'a'] = new TrieNode();

p = p->children[c - 'a'];

}

p->is_word = true;

}

/** Returns if the word is in the trie. */

bool search(const string& word) const {

const TrieNode* p = find(word);

return p && p->is_word;

}

/** Returns if there is any word in the trie that starts with the given prefix. */

bool startsWith(const string& prefix) const {

return find(prefix) != nullptr;

}

private:

struct TrieNode {

TrieNode():is_word(false), children(26, nullptr){}

~TrieNode() {

for (TrieNode* child : children)

if (child) delete child;

}

bool is_word;

vector<TrieNode*> children;

};

const TrieNode* find(const string& prefix) const {

const TrieNode* p = root_.get();

for (const char c : prefix) {

p = p->children[c - 'a'];

if (p == nullptr) break;

}

return p;

}

std::unique_ptr<TrieNode> root_;

};

C++ / hashmap

// Author: Huahua

// Running time: 98 ms

class Trie {

public:

/** Initialize your data structure here. */

Trie(): root_(new TrieNode()) {}

/** Inserts a word into the trie. */

void insert(const string& word) {

TrieNode* p = root_.get();

for (const char c : word) {

if (!p->children.count(c))

p->children[c] = new TrieNode();

p = p->children[c];

}

p->is_word = true;

}

/** Returns if the word is in the trie. */

bool search(const string& word) const {

const TrieNode* p = find(word);

return p && p->is_word;

}

/** Returns if there is any word in the trie that starts with the given prefix. */

bool startsWith(const string& prefix) const {

return find(prefix) != nullptr;

}

private:

struct TrieNode {

TrieNode():is_word(false){}

~TrieNode() {

for (auto& kv : children)

if (kv.second) delete kv.second;

}

bool is_word;

unordered_map<char, TrieNode*> children;

};

const TrieNode* find(const string& prefix) const {

const TrieNode* p = root_.get();

for (const char c : prefix) {

if (!p->children.count(c)) return nullptr;

p = p->children.at(c);

}

return p;

}

std::unique_ptr<TrieNode> root_;

};

Java

// Author: Huahua

// Running time: 184 ms

class Trie {

class TrieNode {

public TrieNode() {

children = new TrieNode[26];

is_word = false;

}

public boolean is_word;

public TrieNode[] children;

}

private TrieNode root;

/** Initialize your data structure here. */

public Trie() {

root = new TrieNode();

}

/** Inserts a word into the trie. */

public void insert(String word) {

TrieNode p = root;

for (int i = 0; i < word.length(); i++) {

int index = (int)(word.charAt(i) - 'a');

if (p.children[index] == null)

p.children[index] = new TrieNode();

p = p.children[index];

}

p.is_word = true;

}

/** Returns if the word is in the trie. */

public boolean search(String word) {

TrieNode node = find(word);

return node != null && node.is_word;

}

/** Returns if there is any word in the trie that starts with the given prefix. */

public boolean startsWith(String prefix) {

TrieNode node = find(prefix);

return node != null;

}

private TrieNode find(String prefix) {

TrieNode p = root;

for(int i = 0; i < prefix.length(); i++) {

int index = (int)(prefix.charAt(i) - 'a');

if (p.children[index] == null) return null;

p = p.children[index];

}

return p;

}

Python 1:

"""

Author: Huahua

Running time: 469 ms

"""

class Trie(object):

class TrieNode(object):

def __init__(self):

self.is_word = False

self.children = [None] * 26

def __init__(self):

self.root = Trie.TrieNode()

def insert(self, word):

p = self.root

for c in word:

index = ord(c) - ord('a')

if not p.children[index]:

p.children[index] = Trie.TrieNode()

p = p.children[index]

p.is_word = True

def search(self, word):

node = self.find(word)

return node is not None and node.is_word

def startsWith(self, prefix):

return self.find(prefix) is not None

def find(self, prefix):

p = self.root

for c in prefix:

index = ord(c) - ord('a')

if not p.children[index]: return None

p = p.children[index]

return p

Python 2:

"""

Author: Huahua

Running time: 212 ms

"""

class Trie(object):

def __init__(self):

self.root = {}

def insert(self, word):

p = self.root

for c in word:

if c not in p:

p[c] = {}

p = p[c]

p['#'] = True

def search(self, word):

node = self.find(word)

return node is not None and '#' in node

def startsWith(self, prefix):

return self.find(prefix) is not None

def find(self, prefix):

p = self.root

for c in prefix:

if c not in p: return None

p = p[c]

return p

花花酱 LeetCode 218. The Skyline Problem

By zxi on September 22, 2017

Problem:

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).

The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .

The output is a list of “key points” (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.

For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].

Notes:

The number of buildings in any input list is guaranteed to be in the range [0, 10000].
The input list is already sorted in ascending order by the left x position Li.
The output list must be sorted by the x position.
There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...[2 3], [4 5], [7 5], [11 5], [12 7]...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...[2 3], [4 5], [12 7], ...]

Idea:

Sweep line

Time Complexity:

O(nlogn)

Space Complexity:

O(n)

Solution1: Heap

C++

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

class Solution {

public:

vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {

// events, x, h, id, type (1=entering, -1=leaving)

vector<Event> events;

int id = 0;

for (const auto& b : buildings) {

events.push_back(Event{id, b[0], b[2], 1});

events.push_back(Event{id, b[1], b[2], -1});

++id;

}

// Sort events by x

sort(events.begin(), events.end());

// Init the heap

MaxHeap heap(buildings.size());

vector<pair<int, int>> ans;

// Process all the events

for (const auto& event: events) {

int x = event.x;

int h = event.h;

int id = event.id;

int type = event.type;

if (type == 1) {

if (h > heap.Max())

ans.emplace_back(x, h);

heap.Add(h, id);

} else {

heap.Remove(id);

if (h > heap.Max())

ans.emplace_back(x, heap.Max());

}

return ans;

}

private:

struct Event {

int id;

int x;

int h;

int type;

// sort by x+, type-, h,

bool operator<(const Event& e) const {

if (x == e.x)

// Entering event h from large to small

// Leaving event h from small to large

return type * h > e.type * e.h;

return x < e.x;

}

};

class MaxHeap {

public:

MaxHeap(int max_items):

idx_(max_items, -1), vals_(max_items), size_(0) {}

// Add an item into the heap. O(log(n))

void Add(int key, int id) {

idx_[id] = size_;

vals_[size_] = {key, id};

++size_;

HeapifyUp(idx_[id]);

}

// Remove an item. O(log(n))

void Remove(int id) {

int idx_to_evict = idx_[id];

// swap with the last element

SwapNode(idx_to_evict, size_ - 1);

--size_;

HeapifyDown(idx_to_evict);

}

bool Empty() const {

return size_ == 0;

}

// Return the max of heap

int Max() const {

return Empty() ? 0 : vals_.front().first;

}

private:

void SwapNode(int i, int j) {

if (i == j) return;

std::swap(idx_[vals_[i].second], idx_[vals_[j].second]);

std::swap(vals_[i], vals_[j]);

}

void HeapifyUp(int i) {

while (i != 0) {

int p = (i - 1) / 2;

if (vals_[i].first <= vals_[p].first)

return;

SwapNode(i, p);

i = p;

}

// Make the heap valid again. O(log(n))

void HeapifyDown(int i) {

while (true) {

int c1 = i*2 + 1;

int c2 = i*2 + 2;

// No child

if (c1 >= size_) return;

// Get the index of the max child

int c = (c2 < size_

&& vals_[c2].first > vals_[c1].first ) ? c2 : c1;

// If key[c] is greater than key[i], swap them and

// continue to HeapifyDown(c)

if (vals_[c].first <= vals_[i].first)

return;

SwapNode(c, i);

i = c;

}

// {key, id}

vector<pair<int,int>> vals_;

// Index of the i-th item in vals_

vector<int> idx_;

int size_;

};

Java

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

// Author: Huahua

// Running time: 91 ms (beats 79.1%)

class Solution {

private MaxHeap heap;

public List<int[]> getSkyline(int[][] buildings) {

int n = buildings.length;

// {x, h, id}

ArrayList<int[]> es = new ArrayList<int[]>();

for (int i = 0; i < n; ++i) {

es.add(new int[]{ buildings[i][0], buildings[i][2], i});

es.add(new int[]{ buildings[i][1], -buildings[i][2], i});

}

es.sort((e1, e2) -> {

return e1[0] == e2[0] ? e2[1] - e1[1] : e1[0] - e2[0]; });

List<int[]> ans = new ArrayList<int[]>();

heap = new MaxHeap(n);

for (int[] e : es) {

int x = e[0];

int h = e[1];

int id = e[2];

Boolean entering = h > 0;

h = Math.abs(h);

if (entering) {

if (h > heap.max())

ans.add(new int[]{x, h});

heap.add(h, id);

} else {

heap.remove(id);

if (h > heap.max())

ans.add(new int[]{x, heap.max()});

}

return ans;

}

private class MaxHeap {

// (key, id)

private List<int[]> nodes;

// idx[i] = index of building[i] in nodes

private int[] idx;

public MaxHeap(int size) {

idx = new int[size];

nodes = new ArrayList<int[]>();

}

public void add(int key, int id) {

idx[id] = nodes.size();

nodes.add(new int[]{key, id});

heapifyUp(idx[id]);

}

public void remove(int id) {

int idx_to_evict = idx[id];

swapNode(idx_to_evict, nodes.size() - 1);

idx[id] = -1;

nodes.remove(nodes.size() - 1);

heapifyUp(idx_to_evict);

heapifyDown(idx_to_evict);

}

public Boolean empty() {

return nodes.isEmpty();

}

public int max() {

return empty() ? 0 : nodes.get(0)[0];

}

private void heapifyUp(int i) {

while (i != 0) {

int p = (i - 1) / 2;

if (nodes.get(i)[0] <= nodes.get(p)[0])

return;

swapNode(i, p);

i = p;

}

private void swapNode(int i, int j) {

int tmpIdx = idx[nodes.get(i)[1]];

idx[nodes.get(i)[1]] = idx[nodes.get(j)[1]];

idx[nodes.get(j)[1]] = tmpIdx;

int[] tmpNode = nodes.get(i);

nodes.set(i, nodes.get(j));

nodes.set(j, tmpNode);

}

private void heapifyDown(int i) {

while (true) {

int c1 = i*2 + 1;

int c2 = i*2 + 2;

if (c1 >= nodes.size()) return;

int c = (c2 < nodes.size()

&& nodes.get(c2)[0] > nodes.get(c1)[0]) ? c2 : c1;

if (nodes.get(c)[0] <= nodes.get(i)[0])

return;

swapNode(c, i);

i = c;

}

Solution 2: Multiset

C++

// Author: Huahua

// Time Complexity: O(nlogn)

// Space Complexity: O(n)

// Running Time: 22 ms

class Solution {

public:

vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {

typedef pair<int, int> Event;

// events, x, h

vector<Event> es;

hs_.clear();

for (const auto& b : buildings) {

es.emplace_back(b[0], b[2]);

es.emplace_back(b[1], -b[2]);

}

// Sort events by x

sort(es.begin(), es.end(), [](const Event& e1, const Event& e2){

if (e1.first == e2.first) return e1.second > e2.second;

return e1.first < e2.first;

});

vector<pair<int, int>> ans;

// Process all the events

for (const auto& e: es) {

int x = e.first;

bool entering = e.second > 0;

int h = abs(e.second);

if (entering) {

if (h > this->maxHeight())

ans.emplace_back(x, h);

hs_.insert(h);

} else {

hs_.erase(hs_.equal_range(h).first);

if (h > this->maxHeight())

ans.emplace_back(x, this->maxHeight());

}

return ans;

}

private:

int maxHeight() const {

if (hs_.empty()) return 0;

return *hs_.rbegin();

}

multiset<int> hs_;

};

花花酱 LeetCode 677. Map Sum Pairs

By zxi on September 18, 2017

https://leetcode.com/problems/map-sum-pairs/description/

Problem:

Implement a MapSum class with insert, and sum methods.

For the method insert, you’ll be given a pair of (string, integer). The string represents the key and the integer represents the value. If the key already existed, then the original key-value pair will be overridden to the new one.

For the method sum, you’ll be given a string representing the prefix, and you need to return the sum of all the pairs’ value whose key starts with the prefix.

Example 1:

Input: insert("apple", 3), Output: Null

Input: sum("ap"), Output: 3

Input: insert("app", 2), Output: Null

Input: sum("ap"), Output: 5

Idea:

Prefix tree

Solution 1

// Author: Huahua

// Running time: 3 ms

class MapSum {

public:

/** Initialize your data structure here. */

MapSum() {}

void insert(const string& key, int val) {

int inc = val;

if (vals_.count(key)) {

inc -= vals_[key];

}

vals_[key] = val;

for (int i = 1; i <= key.length(); ++i)

sums_[key.substr(0,i)] += inc;

}

int sum(const string& prefix) {

return sums_[prefix];

}

private:

unordered_map<string, int> vals_;

unordered_map<string, int> sums_;

};

Solution 2:

class MapSum {

public:

/** Initialize your data structure here. */

MapSum() {}

void insert(string key, int val) {

int inc = val - vals_[key];

Trie* p = &root;

for (const char c : key) {

if (!p->children[c])

p->children[c] = new Trie();

p->children[c]->sum += inc;

p = p->children[c];

}

vals_[key] = val;

}

int sum(string prefix) {

Trie* p = &root;

for (const char c : prefix) {

if (!p->children[c]) return 0;

p = p->children[c];

}

return p->sum;

}

private:

struct Trie {

Trie():children(128, nullptr), sum(0){}

~Trie() {

for (auto child : children)

if (child) delete child;

children.clear();

}

vector<Trie*> children;

int sum;

};

Trie root; // dummy root

unordered_map<string, int> vals_; // key -> val

};

with std::unique_ptr

// Author: Huahua

// Running time: 5 ms

class MapSum {

public:

/** Initialize your data structure here. */

MapSum(): root_(new Trie()) {}

void insert(string key, int val) {

int inc = val - vals_[key];

Trie* p = root_.get();

for (const char c : key) {

if (!p->children[c])

p->children[c] = new Trie();

p->children[c]->sum += inc;

p = p->children[c];

}

vals_[key] = val;

}

int sum(string prefix) {

Trie* p = root_.get();

for (const char c : prefix) {

if (!p->children[c]) return 0;

p = p->children[c];

}

return p->sum;

}

private:

struct Trie {

Trie():children(128, nullptr), sum(0){}

~Trie() {

for (auto child : children)

if (child) {

delete child;

child = nullptr;

}

children.clear();

}

vector<Trie*> children;

int sum;

};

std::unique_ptr<Trie> root_;

unordered_map<string, int> vals_; // key -> val

};

花花酱 LeetCode 381. Insert Delete GetRandom O(1) – Duplicates allowed

By zxi on September 17, 2017

https://leetcode.com/problems/insert-delete-getrandom-o1-duplicates-allowed/description/

Problem:

Design a data structure that supports all following operations in average O(1) time.

Note: Duplicate elements are allowed.

insert(val): Inserts an item val to the collection.
remove(val): Removes an item val from the collection if present.
getRandom: Returns a random element from current collection of elements. The probability of each element being returned is linearly related to the number of same value the collection contains.

Idea:

Hashtable + array

Solution:

// Author: Huahua

// Running time: 49 ms

class RandomizedCollection {

public:

/** Initialize your data structure here. */

RandomizedCollection() {}

/** Inserts a value to the collection. Returns true if the collection did not already contain the specified element. */

bool insert(int val) {

m_[val].push_back(vals_.size());

vals_.emplace_back(val, m_[val].size() - 1);

return m_[val].size() == 1u;

}

/** Removes a value from the collection. Returns true if the collection contained the specified element. */

bool remove(int val) {

if (!m_.count(val)) return false;

int index_to_evict = m_[val].back();

const auto& last_entry = vals_.back();

// Update index

m_[last_entry.first][last_entry.second] = index_to_evict;

// Swap vals

swap(vals_.back(), vals_[index_to_evict]);

// Clenup

vals_.pop_back();

m_[val].pop_back();

if (m_[val].empty()) m_.erase(val);

return true;

}

/** Get a random element from the collection. */

int getRandom() {

return vals_[rand() % vals_.size()].first;

}

private:

// val -> indices array: indices in vals_

unordered_map<int, vector<int>> m_;

// {val, index in the indices array}

vector<pair<int,int>> vals_;

};

Java

// Author: Huahua

// Running time: 122 ms (<94.53%)

class RandomizedCollection {

class Entry {

public int value;

public int index;

public Entry(int val, int idx) {

value = val;

index = idx;

}

private Map<Integer, List<Integer>> m;

private List<Entry> vals;

private Random rand;

/** Initialize your data structure here. */

public RandomizedCollection() {

m = new HashMap<>();

vals = new ArrayList<>();

rand = new Random();

}

/** Inserts a value to the collection. Returns true if the collection did not already contain the specified element. */

public boolean insert(int val) {

List<Integer> l = m.getOrDefault(val, new ArrayList<Integer>());

l.add(vals.size());

m.put(val, l);

vals.add(new Entry(val, l.size() - 1));

return l.size() == 1;

}

/** Removes a value from the collection. Returns true if the collection contained the specified element. */

public boolean remove(int val) {

if (!m.containsKey(val)) return false;

List<Integer> l = m.get(val);

int index_to_evict = l.get(l.size() - 1);

Entry last_entry = vals.get(vals.size() - 1);

// Update index

m.get(last_entry.value).set(last_entry.index, index_to_evict);

// Swap vals

vals.set(index_to_evict, last_entry);

// Cleanup

vals.remove(vals.size() - 1);

l.remove(l.size() - 1);

if (l.size() == 0) m.remove(val);

return true;

}

/** Get a random element from the collection. */

public int getRandom() {

return vals.get(rand.nextInt(vals.size())).value;

}

Related Problems:

花花酱 LeetCode 380. Insert Delete GetRandom O(1)

By zxi on September 16, 2017

Problem:

Design a data structure that supports all following operations in average O(1) time.

insert(val): Inserts an item val to the set if not already present.
remove(val): Removes an item val from the set if present.
getRandom: Returns a random element from current set of elements. Each element must have the same probability of being returned.

Idea:

Hashtable + array

Time complexity:

O(1)

Solution:

// Author: Huahua

// Running time: 49 ms

class RandomizedSet {

public:

/** Initialize your data structure here. */

RandomizedSet() {}

/** Inserts a value to the set. Returns true if the set did not already contain the specified element. */

bool insert(int val) {

if(m_.count(val)) return false;

m_[val] = vals_.size();

vals_.push_back(val);

return true;

}

/** Removes a value from the set. Returns true if the set contained the specified element. */

bool remove(int val) {

if(!m_.count(val)) return false;

int index = m_[val];

m_[vals_.back()] = index;

m_.erase(val);

std::swap(vals_[index], vals_.back());

vals_.pop_back();

return true;

}

/** Get a random element from the set. */

int getRandom() {

int index = rand() % vals_.size();

return vals_[index];

}

private:

// val -> index in the array

unordered_map<int, int> m_;

vector<int> vals_;

};

Related Problems: