Posts published in “Greedy”

花花酱 LeetCode 2405. Optimal Partition of String

By zxi on September 11, 2022

Given a string s, partition the string into one or more substrings such that the characters in each substring are unique. That is, no letter appears in a single substring more than once.

Return the minimum number of substrings in such a partition.

Note that each character should belong to exactly one substring in a partition.

Example 1:

Input: s = "abacaba"
Output: 4
Explanation:
Two possible partitions are ("a","ba","cab","a") and ("ab","a","ca","ba").
It can be shown that 4 is the minimum number of substrings needed.

Example 2:

Input: s = "ssssss"
Output: 6
Explanation:
The only valid partition is ("s","s","s","s","s","s").

Constraints:

1 <= s.length <= 10⁵
s consists of only English lowercase letters.

Solution: Greedy

Extend the cur string as long as possible unless a duplicate character occurs.

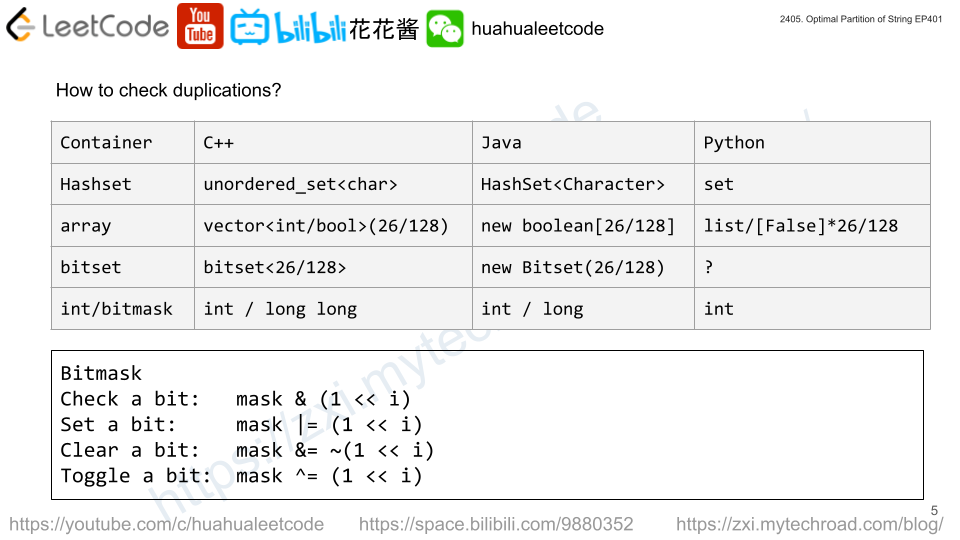
You can use hashtable / array or bitmask to mark whether a character has been seen so far.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int partitionString(string s) {

unordered_set<char> m;

int ans = 0;

for (char c : s) {

if (m.insert(c).second) continue;

m.clear();

m.insert(c);

++ans;

}

return ans + 1;

}

};

C++

// Author: Huahua

class Solution {

public:

int partitionString(string s) {

vector<int> m(26);

int ans = 0;

for (char c : s) {

if (++m[c - 'a'] == 1) continue;

fill(begin(m), end(m), 0);

m[c - 'a'] = 1;

++ans;

}

return ans + 1;

}

};

C++

// Author: Huahua

class Solution {

public:

int partitionString(string s) {

int mask = 0;

int ans = 0;

for (char c : s) {

if (mask & (1 << (c - 'a'))) {

mask = 0;

++ans;

}

mask |= 1 << (c - 'a');

}

return ans + 1;

}

};

花花酱 LeetCode 2242. Maximum Score of a Node Sequence

By zxi on April 16, 2022

There is an undirected graph with n nodes, numbered from 0 to n - 1.

You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

A node sequence is valid if it meets the following conditions:

There is an edge connecting every pair of adjacent nodes in the sequence.
No node appears more than once in the sequence.

The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return -1.

Example 1:

Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

Example 2:

Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.

Constraints:

n == scores.length
4 <= n <= 5 * 10⁴
1 <= scores[i] <= 10⁸
0 <= edges.length <= 5 * 10⁴
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no duplicate edges.

Solution: Greedy / Top3 neighbors

Since |E| is already 5*10⁴, we can’t enumerate all possible sequences. We must do in O(|E|) or O(|E|log|E|).

Enumerate all the edges, we have a pair of node a, b. To get the optimal answer, we just need to find the largest neighbor of a and b, which we call c, d respectively. Just need to make sure a, b, c, d are unique. i.e. c != d, c != b and d != a. Since the a’s largest neighbor can be either b or d. We can’t just store the largest neighbor, but top 3 instead for each node to avoid duplications.

Time complexity: O(|E|*9)
Space complexity: O(|V|*3)

C++

// Author: Huahua

class Solution {

public:

int maximumScore(vector<int>& scores, vector<vector<int>>& edges) {

const int n = scores.size();

vector<set<pair<int, int>>> top3(n);

for (const auto& e : edges) {

top3[e[0]].emplace(scores[e[1]], e[1]);

top3[e[1]].emplace(scores[e[0]], e[0]);

if (top3[e[0]].size() > 3) top3[e[0]].erase(begin(top3[e[0]]));

if (top3[e[1]].size() > 3) top3[e[1]].erase(begin(top3[e[1]]));

}

int ans = -1;

for (const auto& e : edges) {

const int a = e[0], b = e[1], sa = scores[a], sb = scores[b];

for (const auto& [sc, c] : top3[a])

for (const auto& [sd, d] : top3[b])

if (sa + sb + sc + sd > ans && c != b && c != d && d != a)

ans = sa + sb + sc + sd;

}

return ans;

}

};

花花酱 LeetCode 2224. Minimum Number of Operations to Convert Time

By zxi on April 2, 2022

You are given two strings current and correct representing two 24-hour times.

24-hour times are formatted as "HH:MM", where HH is between 00 and 23, and MM is between 00 and 59. The earliest 24-hour time is 00:00, and the latest is 23:59.

In one operation you can increase the time current by 1, 5, 15, or 60 minutes. You can perform this operation any number of times.

Return the minimum number of operations needed to convert current to correct.

Example 1:

Input: current = "02:30", correct = "04:35"
Output: 3
Explanation:
We can convert current to correct in 3 operations as follows:
- Add 60 minutes to current. current becomes "03:30".
- Add 60 minutes to current. current becomes "04:30".
- Add 5 minutes to current. current becomes "04:35".
It can be proven that it is not possible to convert current to correct in fewer than 3 operations.

Example 2:

Input: current = "11:00", correct = "11:01"
Output: 1
Explanation: We only have to add one minute to current, so the minimum number of operations needed is 1.

Constraints:

current and correct are in the format "HH:MM"
current <= correct

Solution: Greedy

Start with 60, then 15, 5 and finally increase 1 minute a time.

Time complexity: O(1)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int convertTime(string current, string correct) {

auto getMinute = [](string_view t) {

return (t[0] - '0') * 10 * 60

+ (t[1] - '0') * 60

+ (t[3] - '0') * 10

+ (t[4] - '0');

};

int t1 = getMinute(current);

int t2 = getMinute(correct);

int ans = 0;

for (int d : {60, 15, 5, 1})

while (t2 - t1 >= d) {

++ans;

t1 += d;

}

return ans;

}

};

花花酱 LeetCode 2195. Append K Integers With Minimal Sum

By zxi on March 8, 2022

You are given an integer array nums and an integer k. Append k unique positive integers that do not appear in nums to nums such that the resulting total sum is minimum.

Return the sum of the k integers appended to nums.

Example 1:

Input: nums = [1,4,25,10,25], k = 2
Output: 5
Explanation: The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.

Example 2:

Input: nums = [5,6], k = 6
Output: 25
Explanation: The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum. 
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.

Constraints:

1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁹
1 <= k <= 10⁸

Solution: Greedy + Math, fill the gap

Sort all the numbers and remove duplicated ones, and fill the gap between two neighboring numbers.
e.g. [15, 3, 8, 8] => sorted = [3, 8, 15]
fill 0->3, 1,2, sum = ((0 + 1) + (3-1)) * (3-0-1) / 2 = 3
fill 3->8, 4, 5, 6, 7, sum = ((3 + 1) + (8-1)) * (8-3-1) / 2 = 22
fill 8->15, 9, 10, …, 14, …
fill 15->inf, 16, 17, …

Time complexity: O(nlogn)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

long long minimalKSum(vector<int>& nums, int k) {

sort(begin(nums), end(nums));

long long ans = 0;

long long p = 0;

for (int c : nums) {

if (c == p) continue;

long long n = min((long long)k, c - p - 1);

ans += (p + 1 + p + n) * n / 2;

k -= n;

p = c;

}

ans += (p + 1 + p + k) * k / 2;

return ans;

}

};

花花酱 LeetCode 2178. Maximum Split of Positive Even Integers

By zxi on March 4, 2022

You are given an integer finalSum. Split it into a sum of a maximum number of unique positive even integers.

For example, given finalSum = 12, the following splits are valid (unique positive even integers summing up to finalSum): (12), (2 + 10), (2 + 4 + 6), and (4 + 8). Among them, (2 + 4 + 6) contains the maximum number of integers. Note that finalSum cannot be split into (2 + 2 + 4 + 4) as all the numbers should be unique.

Return a list of integers that represent a valid split containing a maximum number of integers. If no valid split exists for finalSum, return an empty list. You may return the integers in any order.

Example 1:

Input: finalSum = 12
Output: [2,4,6]
Explanation: The following are valid splits: (12), (2 + 10), (2 + 4 + 6), and (4 + 8).
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return [2,4,6].
Note that [2,6,4], [6,2,4], etc. are also accepted.

Example 2:

Input: finalSum = 7
Output: []
Explanation: There are no valid splits for the given finalSum.
Thus, we return an empty array.

Example 3:

Input: finalSum = 28
Output: [6,8,2,12]
Explanation: The following are valid splits: (2 + 26), (6 + 8 + 2 + 12), and (4 + 24). 
(6 + 8 + 2 + 12) has the maximum number of integers, which is 4. Thus, we return [6,8,2,12].
Note that [10,2,4,12], [6,2,4,16], etc. are also accepted.

Constraints:

1 <= finalSum <= 10¹⁰

Solution: Greedy

The get the maximum number of elements, we must use the smallest numbers.

[2, 4, 6, …, 2k, x], where x > 2k
let s = 2 + 4 + … + 2k, x = num – s
since num is odd and s is also odd, so thus x = num – s.

Time complexity: O(sqrt(num)) for constructing outputs.
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<long long> maximumEvenSplit(long long finalSum) {

if (finalSum & 1) return {};

vector<long long> ans;

long long s = 0;

for (long long i = 2; s + i <= finalSum; s += i, i += 2)

ans.push_back(i);

ans.back() += (finalSum - s);

return ans;

}

};