花花酱 LeetCode 2242. Maximum Score of a Node Sequence

There is an undirected graph with n nodes, numbered from 0 to n - 1.

You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

A node sequence is valid if it meets the following conditions:

• There is an edge connecting every pair of adjacent nodes in the sequence.
• No node appears more than once in the sequence.

The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return -1.

Example 1:

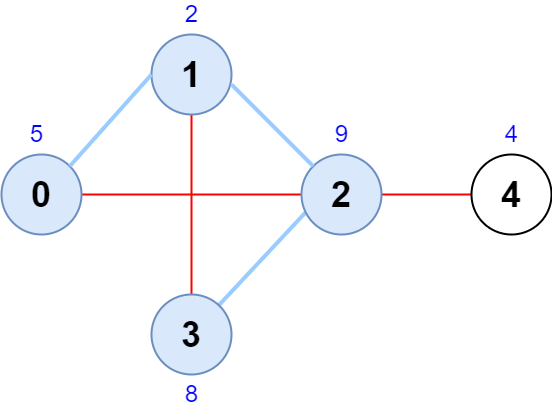
Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

Example 2:

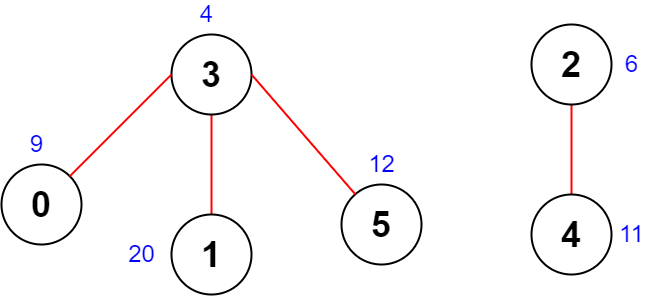
Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.

Constraints:

• n == scores.length
• 4 <= n <= 5 * 104
• 1 <= scores[i] <= 108
• 0 <= edges.length <= 5 * 104
• edges[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no duplicate edges.

Solution: Greedy / Top3 neighbors

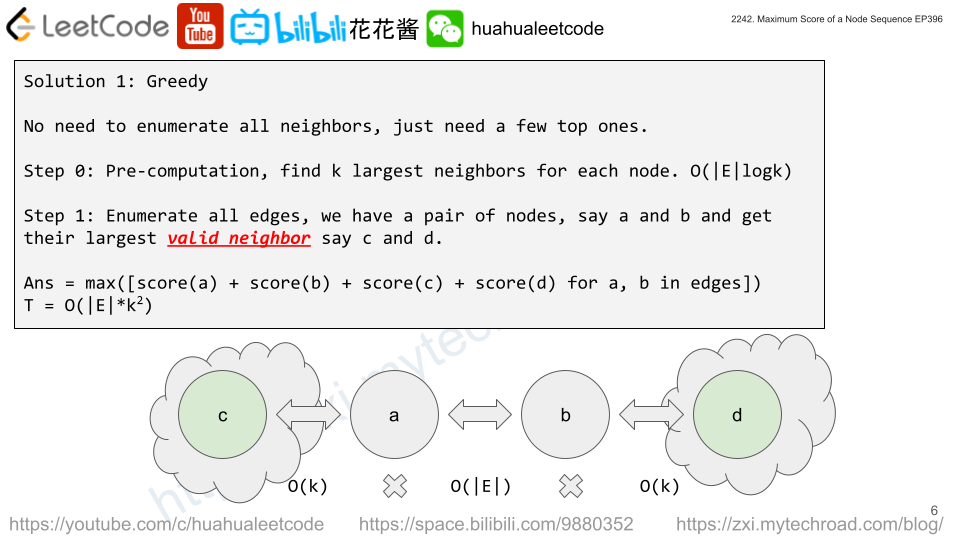
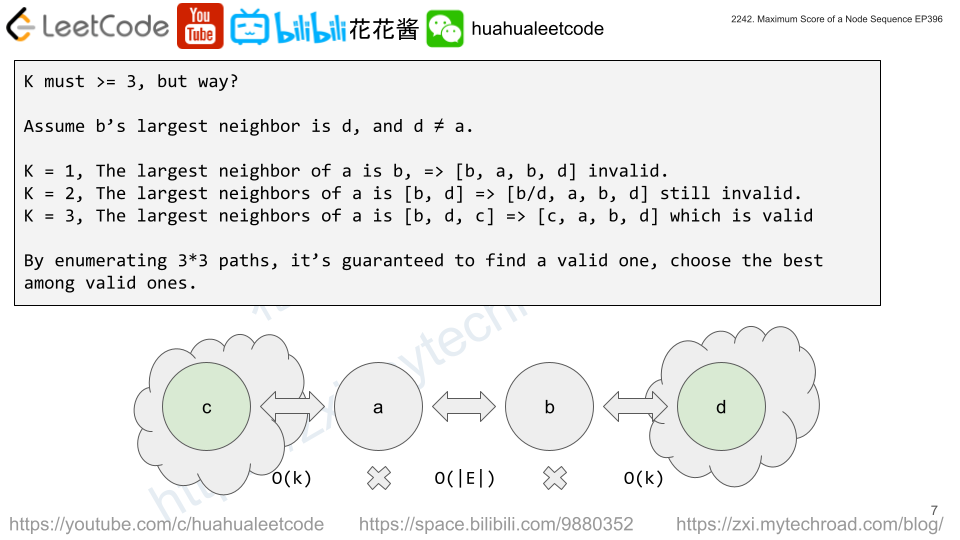
Since |E| is already 5*10⁴, we can’t enumerate all possible sequences. We must do in O(|E|) or O(|E|log|E|).

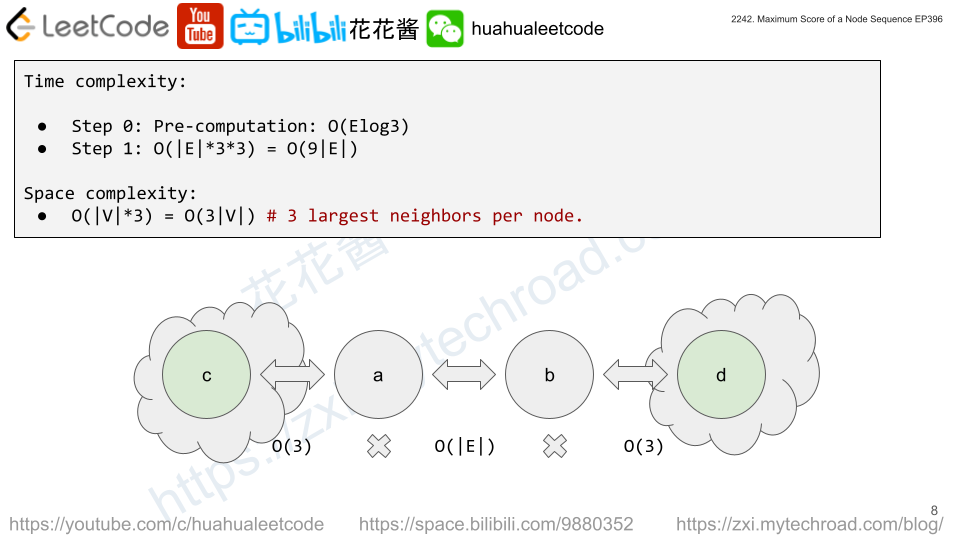
Enumerate all the edges, we have a pair of node a, b. To get the optimal answer, we just need to find the largest neighbor of a and b, which we call c, d respectively. Just need to make sure a, b, c, d are unique. i.e. c != d, c != b and d != a. Since the a’s largest neighbor can be either b or d. We can’t just store the largest neighbor, but top 3 instead for each node to avoid duplications.

Time complexity: O(|E|*9)
Space complexity: O(|V|*3)