Press "Enter" to skip to content

Posts published in “List”

花花酱 LeetCode 160. Intersection of Two Linked Lists

By zxi on November 28, 2021

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:

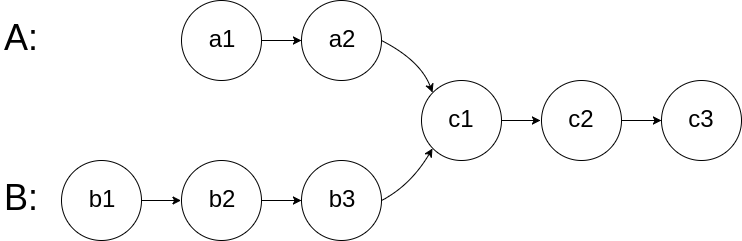
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

  • intersectVal – The value of the node where the intersection occurs. This is 0 if there is no intersected node.
  • listA – The first linked list.
  • listB – The second linked list.
  • skipA – The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
  • skipB – The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.

The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.

Example 1:

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

Example 2:

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

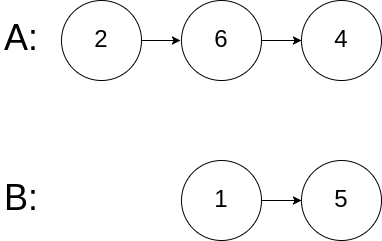
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Constraints:

  • The number of nodes of listA is in the m.
  • The number of nodes of listB is in the n.
  • 0 <= m, n <= 3 * 104
  • 1 <= Node.val <= 105
  • 0 <= skipA <= m
  • 0 <= skipB <= n
  • intersectVal is 0 if listA and listB do not intersect.
  • intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

Follow up: Could you write a solution that runs in O(n) time and use only O(1) memory?

Solution 1: Two Passes by swapping heads

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 142. Linked List Cycle II

By zxi on November 28, 2021

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

  • The number of the nodes in the list is in the range [0, 104].
  • -105 <= Node.val <= 105
  • pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Solution 1: Hashtset

Time complexity: O(n)
Space complexity: O(n)

C++

Solution: Fast slow pointers

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 109. Convert Sorted List to Binary Search Tree

By zxi on November 27, 2021

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []
Output: []

Example 3:

Input: head = [0]
Output: [0]

Example 4:

Input: head = [1,3]
Output: [3,1]

Constraints:

  • The number of nodes in head is in the range [0, 2 * 104].
  • -105 <= Node.val <= 105

Solution 1: Recursion w/ Fast + Slow Pointers

For each sublist, use fast/slow pointers to find the mid and build the tree.

Time complexity: O(nlogn)
Space complexity: O(logn)

C++

花花酱 LeetCode 2074. Reverse Nodes in Even Length Groups

By zxi on November 15, 2021

You are given the head of a linked list.

The nodes in the linked list are sequentially assigned to non-empty groups whose lengths form the sequence of the natural numbers (1, 2, 3, 4, ...). The length of a group is the number of nodes assigned to it. In other words,

  • The 1st node is assigned to the first group.
  • The 2nd and the 3rd nodes are assigned to the second group.
  • The 4th, 5th, and 6th nodes are assigned to the third group, and so on.

Note that the length of the last group may be less than or equal to 1 + the length of the second to last group.

Reverse the nodes in each group with an even length, and return the head of the modified linked list.

Example 1:

Input: head = [5,2,6,3,9,1,7,3,8,4]
Output: [5,6,2,3,9,1,4,8,3,7]
Explanation:
- The length of the first group is 1, which is odd, hence no reversal occurrs.
- The length of the second group is 2, which is even, hence the nodes are reversed.
- The length of the third group is 3, which is odd, hence no reversal occurrs.
- The length of the last group is 4, which is even, hence the nodes are reversed.

Example 2:

Input: head = [1,1,0,6]
Output: [1,0,1,6]
Explanation:
- The length of the first group is 1. No reversal occurrs.
- The length of the second group is 2. The nodes are reversed.
- The length of the last group is 1. No reversal occurrs.

Example 3:

Input: head = [2,1]
Output: [2,1]
Explanation:
- The length of the first group is 1. No reversal occurrs.
- The length of the last group is 1. No reversal occurrs.

Example 4:

Input: head = [8]
Output: [8]
Explanation: There is only one group whose length is 1. No reversal occurrs.

Constraints:

  • The number of nodes in the list is in the range [1, 105].
  • 0 <= Node.val <= 105

Solution: List

Reuse ReverseList from 花花酱 LeetCode 206. Reverse Linked List

Time complexity: O(n)
Space complexity: O(1)

C++

LeetCode 2058. Find the Minimum and Maximum Number of Nodes Between Critical Points

By zxi on November 3, 2021

A critical point in a linked list is defined as either a local maxima or a local minima.

A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.

A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.

Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.

Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].

Example 1:

Input: head = [3,1]
Output: [-1,-1]
Explanation: There are no critical points in [3,1].

Example 2:

Input: head = [5,3,1,2,5,1,2]
Output: [1,3]
Explanation: There are three critical points:
- [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2.
- [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1.
- [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2.
The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1.
The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.

Example 3:

Input: head = [1,3,2,2,3,2,2,2,7]
Output: [3,3]
Explanation: There are two critical points:
- [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2.
- [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2.
Both the minimum and maximum distances are between the second and the fifth node.
Thus, minDistance and maxDistance is 5 - 2 = 3.
Note that the last node is not considered a local maxima because it does not have a next node.

Example 4:

Input: head = [2,3,3,2]
Output: [-1,-1]
Explanation: There are no critical points in [2,3,3,2].

Constraints:

  • The number of nodes in the list is in the range [2, 105].
  • 1 <= Node.val <= 105

Solution: One Pass

Track the first and last critical points.

Time complexity: O(n)
Space complexity: O(1)

C++