Given the array nums consisting of n positive integers. You computed the sum of all non-empty continous subarrays from the array and then sort them in non-decreasing order, creating a new array of n * (n + 1) / 2 numbers.
Return the sum of the numbers from index left to index right (indexed from 1), inclusive, in the new array. Since the answer can be a huge number return it modulo 10^9 + 7.
Example 1:
Input: nums = [1,2,3,4], n = 4, left = 1, right = 5 Output: 13 Explanation: All subarray sums are 1, 3, 6, 10, 2, 5, 9, 3, 7, 4. After sorting them in non-decreasing order we have the new array [1, 2, 3, 3, 4, 5, 6, 7, 9, 10]. The sum of the numbers from index le = 1 to ri = 5 is 1 + 2 + 3 + 3 + 4 = 13.
Example 2:
Input: nums = [1,2,3,4], n = 4, left = 3, right = 4 Output: 6 Explanation: The given array is the same as example 1. We have the new array [1, 2, 3, 3, 4, 5, 6, 7, 9, 10]. The sum of the numbers from index le = 3 to ri = 4 is 3 + 3 = 6.
Example 3:
Input: nums = [1,2,3,4], n = 4, left = 1, right = 10 Output: 50
Constraints:
1 <= nums.length <= 10^3nums.length == n1 <= nums[i] <= 1001 <= left <= right <= n * (n + 1) / 2
Solution 1: Brute Force
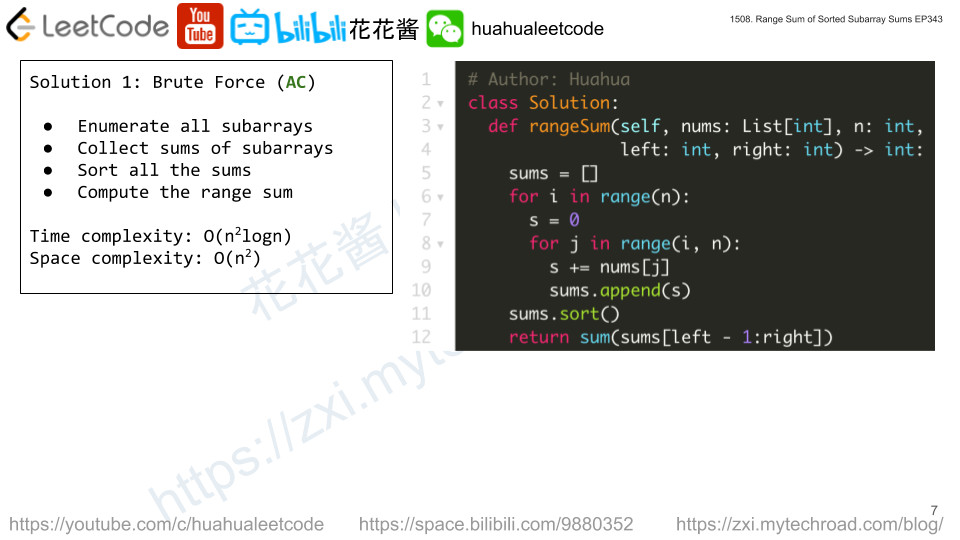
Find sums of all the subarrays and sort the values.
Time complexity: O(n^2logn)
Space complexity: O(n^2)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
// Author: Huahua class Solution { public: int rangeSum(vector<int>& nums, int n, int left, int right) { constexpr int kMod = 1e9 + 7; vector<int> sums; for (int i = 0; i < n; ++i) for (int j = i, sum = 0; j < n; ++j) sums.push_back(sum += nums[j]); sort(begin(sums), end(sums)); return accumulate(begin(sums) + left - 1, begin(sums) + right, 0LL) % kMod; } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
// Author: Huahua class Solution { public int rangeSum(int[] nums, int n, int left, int right) { final int kMod = (int)(1e9 + 7); int[] sums = new int[n * (n + 1) / 2]; int idx = 0; for (int i = 0; i < n; ++i) for (int j = i, sum = 0; j < n; ++j, ++idx) sums[idx] = sum += nums[j]; Arrays.sort(sums); int ans = 0; for (int i = left; i <= right; ++i) ans = (ans + sums[i - 1]) % kMod; return ans; } } |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 |
# Author: Huahua class Solution: def rangeSum(self, nums: List[int], n: int, left: int, right: int) -> int: sums = [] for i in range(n): s = 0 for j in range(i, n): s += nums[j] sums.append(s) sums.sort() return sum(sums[left - 1:right]) |
Solution 2: Priority Queue / Min Heap
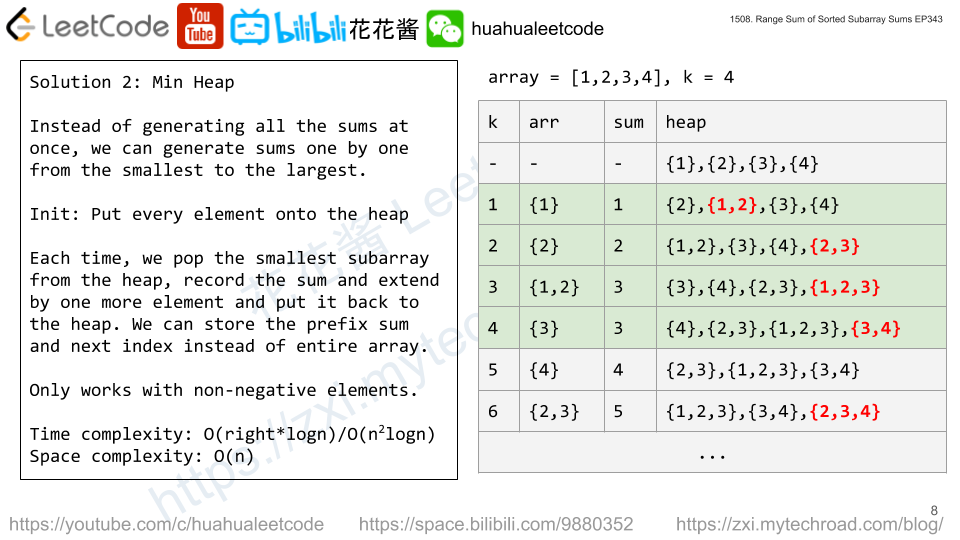
For each subarray, start with one element e.g nums[i], put them into a priority queue (min heap). Each time, we have the smallest subarray sum, and extend that subarray and put the new sum back into priority queue. Thought it has the same time complexity as the brute force one in worst case, but space complexity can be reduce to O(n).
Time complexity: O(n^2logn)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
struct Entry { int sum; int i; bool operator<(const Entry& e) const { return sum > e.sum; } }; class Solution { public: int rangeSum(vector<int>& nums, int n, int left, int right) { constexpr int kMod = 1e9 + 7; priority_queue<Entry> q; // Sort by e.sum in descending order. for (int i = 0; i < n; ++i) q.push({nums[i], i}); long ans = 0; for (int j = 1; j <= right; ++j) { const auto e = std::move(q.top()); q.pop(); if (j >= left) ans += e.sum; if (e.i + 1 < n) q.push({e.sum + nums[e.i + 1], e.i + 1}); } return ans % kMod; } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import java.util.AbstractMap; class Solution { public int rangeSum(int[] nums, int n, int left, int right) { final int kMod = (int)(1e9 + 7); var q = new PriorityQueue<Map.Entry<Integer, Integer>>((a, b) -> a.getKey() - b.getKey()); for (int i = 0; i < n; ++i) q.offer(new AbstractMap.SimpleEntry<>(nums[i], i)); int ans = 0; for (int k = 1; k <= right; ++k) { var e = q.poll(); int sum = e.getKey(); int i = e.getValue(); if (k >= left) ans = (ans + sum) % kMod; if (i + 1 < n) q.offer(new AbstractMap.SimpleEntry<>(sum + nums[i + 1], i + 1)); } return ans; } } |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# Author: Huahua class Solution: def rangeSum(self, nums: List[int], n: int, left: int, right: int) -> int: q = [(num, i) for i, num in enumerate(nums)] heapq.heapify(q) ans = 0 for k in range(1, right + 1): s, i = heapq.heappop(q) if k >= left: ans += s if i + 1 < n: heapq.heappush(q, (s + nums[i + 1], i + 1)) return ans % int(1e9 + 7) |
Solution 3: Binary Search + Sliding Window


Use binary search to find S s.t. that there are at least k subarrys have sum <= S.
Given S, we can use sliding window to count how many subarrays have sum <= S and their total sum.
ans = sums_of_first(right) – sums_of_first(left – 1).
Time complexity: O(n * log(sum(nums))
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
// Author: Huahua class Solution { public: int rangeSum(vector<int>& nums, int n, int left, int right) { constexpr int kMod = 1e9 + 7; // Returns number of subarrays that have // sum <= target and their total sum. auto countAndSum = [&](int target) -> pair<int, long> { int count = 0; long cur = 0; long sum = 0; long total_sum = 0; for (long j = 0, i = 0; j < n; ++j) { cur += nums[j]; sum += nums[j] * (j - i + 1); while (cur > target) { sum -= cur; cur -= nums[i++]; } count += j - i + 1; total_sum += sum; } return {count, total_sum}; }; // Returns the total sums of smallest k subarrays. // Use binary search to find the smallest sum l s.t. // there are at least k of subarrays have sums <= l. const int min_sum = *min_element(begin(nums), end(nums)); const int max_sum = accumulate(begin(nums), end(nums), 0) + 1; auto sumOfFirstK = [&](int k) -> long { int l = min_sum; int r = max_sum; while (l < r) { int mid = l + (r - l) / 2; if (countAndSum(mid).first >= k) r = mid; else l = mid + 1; } const auto [count, sum] = countAndSum(l); // There can be more subarrays have the same sum of l. return sum - l * (count - k); }; return (sumOfFirstK(right) - sumOfFirstK(left - 1)) % kMod; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment