花花酱 LeetCode 1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit

Given an array of integers nums and an integer limit, return the size of the longest continuous subarray such that the absolute difference between any two elements is less than or equal to limit.

In case there is no subarray satisfying the given condition return 0.

Example 1:

Input: nums = [8,2,4,7], limit = 4
Output: 2 
Explanation: All subarrays are: 
[8] with maximum absolute diff |8-8| = 0 <= 4.
[8,2] with maximum absolute diff |8-2| = 6 > 4. 
[8,2,4] with maximum absolute diff |8-2| = 6 > 4.
[8,2,4,7] with maximum absolute diff |8-2| = 6 > 4.
[2] with maximum absolute diff |2-2| = 0 <= 4.
[2,4] with maximum absolute diff |2-4| = 2 <= 4.
[2,4,7] with maximum absolute diff |2-7| = 5 > 4.
[4] with maximum absolute diff |4-4| = 0 <= 4.
[4,7] with maximum absolute diff |4-7| = 3 <= 4.
[7] with maximum absolute diff |7-7| = 0 <= 4. 
Therefore, the size of the longest subarray is 2.

Example 2:

Input: nums = [10,1,2,4,7,2], limit = 5
Output: 4 
Explanation: The subarray [2,4,7,2] is the longest since the maximum absolute diff is |2-7| = 5 <= 5.

Example 3:

Input: nums = [4,2,2,2,4,4,2,2], limit = 0
Output: 3

Constraints:

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^9
• 0 <= limit <= 10^9

Solution 1: Sliding Window + TreeSet

Use a treeset to maintain a range of [l, r] such that max(nums[l~r]) – min(nums[l~r]) <= limit.
Every time, we add nums[r] into the tree, and move l towards r to keep the max diff under limit.

Time complexity: O(nlogn)
Space complexity: O(n)

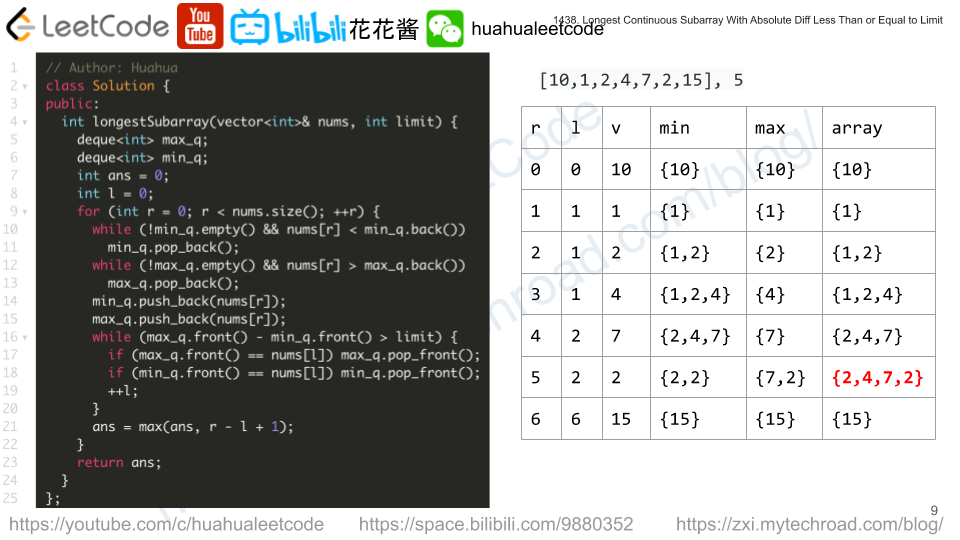
Solution 2: Dual Monotonic Queue

Similar to https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-1425-constrained-subset-sum/

We want to maintain a range [l, r] that max(nums[l~r]) – min(nums[l~r]) <= limit, to track the max/min of a range efficiently we could use monotonic queue. One for max and one for min.

Time complexity: O(n)
Space complexity: O(n)