Posts published in “Uncategorized”

花花酱 LeetCode 2641. Cousins in Binary Tree II

By zxi on April 29, 2023

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins’ values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

Example 1:

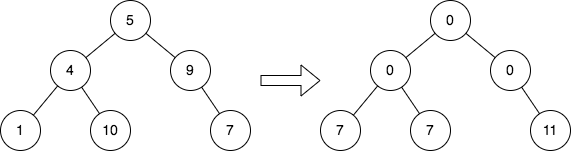
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
1 <= Node.val <= 10⁴

Solution: Level Order Sum

Time complexity: O(n)
Space complexity: O(n)

DFS, two passes

C++

// Author: Huahua

class Solution {

public:

TreeNode* replaceValueInTree(TreeNode* root) {

unordered_map<TreeNode*, int> parentSum;

parentSum[nullptr] = root->val;

vector<int> levelSums;

function<void(TreeNode*, int)> dfs = [&](TreeNode* node, int depth) {

if (!node) return;

if (levelSums.size() <= depth) {

levelSums.push_back(0);

}

levelSums[depth] += node->val;

if (node->left) {

parentSum[node] += node->left->val;

dfs(node->left, depth + 1);

}

if (node->right) {

parentSum[node] += node->right->val;

dfs(node->right, depth + 1);

}

};

function<void(TreeNode*, TreeNode*, int)> dfs2 =

[&](TreeNode* node, TreeNode* p, int depth) {

if (!node) return;

node->val = levelSums[depth] - parentSum[p];

dfs2(node->left, node, depth + 1);

dfs2(node->right, node, depth + 1);

};

dfs(root, 0);

dfs2(root, nullptr, 0);

return root;

}

};

BFS, one+ pass

C++

// Author: Huahua

class Solution {

public:

TreeNode* replaceValueInTree(TreeNode* root) {

root->val = 0;

queue<TreeNode*> q({root});

while (!q.empty()) {

vector<TreeNode*> nodes;

int sum = 0;

for (int s = q.size(); s; --s) {

TreeNode* node = q.front(); q.pop();

nodes.push_back(node);

if (node->left) {

q.push(node->left);

sum += node->left->val;

}

if (node->right) {

q.push(node->right);

sum += node->right->val;

}

for (TreeNode* node : nodes) {

int val = sum - (node->left ? node->left->val : 0)

- (node->right ? node->right->val : 0);

if (node->left) node->left->val = val;

if (node->right) node->right->val = val;

}

return root;

}

};

花花酱 LeetCode 2523. Closest Prime Numbers in Range EP407

By zxi on December 31, 2022

Given two positive integers left and right, find the two integers num1 and num2 such that:

left <= nums1 < nums2 <= right .
nums1 and nums2 are both prime numbers.
nums2 - nums1 is the minimum amongst all other pairs satisfying the above conditions.

Return the positive integer array ans = [nums1, nums2]. If there are multiple pairs satisfying these conditions, return the one with the minimum nums1 value or [-1, -1] if such numbers do not exist.

A number greater than 1 is called prime if it is only divisible by 1 and itself.

Example 1:

Input: left = 10, right = 19
Output: [11,13]
Explanation: The prime numbers between 10 and 19 are 11, 13, 17, and 19.
The closest gap between any pair is 2, which can be achieved by [11,13] or [17,19].
Since 11 is smaller than 17, we return the first pair.

Example 2:

Input: left = 4, right = 6
Output: [-1,-1]
Explanation: There exists only one prime number in the given range, so the conditions cannot be satisfied.

Constraints:

1 <= left <= right <= 10⁶

Solution: Sieve of Eratosthenes

Use Sieve of Eratosthenes to find all primes in range [0, right].

Check neighbor primes and find the best pair.

Time complexity: O(nloglogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> closestPrimes(int left, int right) {

vector<int> primes(right + 1, 1);

primes[0] = primes[1] = 0;

for (int i = 2; i <= sqrt(right); ++i) {

if (!primes[i]) continue;

for (int x = i * i; x <= right; x += i)

primes[x] = 0;

}

vector<int> ans{-1,-1};

for (int i = left, last = -1, best = INT_MAX; i <= right; ++i) {

if (!primes[i]) continue;

if (last > 0 && i - last < best) {

best = i - last;

ans = {last, i};

}

last = i;

}

return ans;

}

};

花花酱 LeetCode 2259. Remove Digit From Number to Maximize Result

By zxi on May 3, 2022

You are given a string number representing a positive integer and a character digit.

Return the resulting string after removing exactly one occurrence of digit from number such that the value of the resulting string in decimal form is maximized. The test cases are generated such that digit occurs at least once in number.

Example 1:

Input: number = "123", digit = "3"
Output: "12"
Explanation: There is only one '3' in "123". After removing '3', the result is "12".

Example 2:

Input: number = "1231", digit = "1"
Output: "231"
Explanation: We can remove the first '1' to get "231" or remove the second '1' to get "123".
Since 231 > 123, we return "231".

Example 3:

Input: number = "551", digit = "5"
Output: "51"
Explanation: We can remove either the first or second '5' from "551".
Both result in the string "51".

Constraints:

2 <= number.length <= 100
number consists of digits from '1' to '9'.
digit is a digit from '1' to '9'.
digit occurs at least once in number.

Solution 1: Brute Force

Try all possible resulting strings.

Time complexity: O(n²)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

string removeDigit(string number, char digit) {

const int n = number.size();

string ans(number.size() - 1, '1');

for (int i = 0; i < n; ++i)

if (number[i] == digit)

ans = max(ans, number.substr(0, i) + number.substr(i + 1));

return ans;

}

};

花花酱 LeetCode 2217. Find Palindrome With Fixed Length

By zxi on March 28, 2022

Given an integer array queries and a positive integer intLength, return an array answer where answer[i] is either the queries[i]^th smallest positive palindrome of length intLength or -1 if no such palindrome exists.

A palindrome is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.

Example 1:

Input: queries = [1,2,3,4,5,90], intLength = 3
Output: [101,111,121,131,141,999]
Explanation:
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90^th palindrome of length 3 is 999.

Example 2:

Input: queries = [2,4,6], intLength = 4
Output: [1111,1331,1551]
Explanation:
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.

Constraints:

1 <= queries.length <= 5 * 10⁴
1 <= queries[i] <= 10⁹
1 <= intLength <= 15

Solution: Math

For even length e.g. 4, we work with length / 2, e.g. 2. Numbers: 10, 11, 12, …, 99, starting from 10, ends with 99, which consist of 99 – 10 + 1 = 90 numbers. For the x-th number, e.g. 88, the left part is 10 + 88 – 1 = 97, just mirror it o get the palindrome. 97|79. Thus we can answer a query in O(k/2) time which is critical.

For odd length e.g. 3 we work with length / 2 + 1, e.g. 2, Numbers: 10, 11, 12, 99. Drop the last digit and mirror the left part to get the palindrome. 101, 111, 121, …, 999.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<long long> kthPalindrome(vector<int>& queries, int k) {

long long s = pow(10, (k + 1) / 2 - 1);

long long e = s * 10;

auto gen = [](long long x, bool isOdd) {

long long ans = x;

for (long long c = isOdd ? x / 10 : x; c; c /= 10)

ans = ans * 10 + c % 10;

return ans;

};

vector<long long> ans;

for (int q : queries)

ans.push_back(q > e - s ? -1 : gen(s + q - 1, k & 1));

return ans;

}

};

花花酱 LeetCode 2120. Execution of All Suffix Instructions Staying in a Grid

By zxi on December 26, 2021

There is an n x n grid, with the top-left cell at (0, 0) and the bottom-right cell at (n - 1, n - 1). You are given the integer n and an integer array startPos where startPos = [start_row, start_col] indicates that a robot is initially at cell (start_row, start_col).

You are also given a 0-indexed string s of length m where s[i] is the i^th instruction for the robot: 'L' (move left), 'R' (move right), 'U' (move up), and 'D' (move down).

The robot can begin executing from any i^th instruction in s. It executes the instructions one by one towards the end of s but it stops if either of these conditions is met:

The next instruction will move the robot off the grid.
There are no more instructions left to execute.

Return an array answer of length m where answer[i] is the number of instructions the robot can execute if the robot begins executing from the i^th instruction in s.

Example 1:

Input: n = 3, startPos = [0,1], s = "RRDDLU"
Output: [1,5,4,3,1,0]
Explanation: Starting from startPos and beginning execution from the i^th instruction:
- 0^th: "RRDDLU". Only one instruction "R" can be executed before it moves off the grid.
- 1^st:  "RDDLU". All five instructions can be executed while it stays in the grid and ends at (1, 1).
- 2^nd:   "DDLU". All four instructions can be executed while it stays in the grid and ends at (1, 0).
- 3^rd:    "DLU". All three instructions can be executed while it stays in the grid and ends at (0, 0).
- 4^th:     "LU". Only one instruction "L" can be executed before it moves off the grid.
- 5^th:      "U". If moving up, it would move off the grid.

Example 2:

Input: n = 2, startPos = [1,1], s = "LURD"
Output: [4,1,0,0]
Explanation:
- 0^th: "LURD".
- 1^st:  "URD".
- 2^nd:   "RD".
- 3^rd:    "D".

Example 3:

Input: n = 1, startPos = [0,0], s = "LRUD"
Output: [0,0,0,0]
Explanation: No matter which instruction the robot begins execution from, it would move off the grid.

Constraints:

m == s.length
1 <= n, m <= 500
startPos.length == 2
0 <= start_row, start_col < n
s consists of 'L', 'R', 'U', and 'D'.

Solution: Simulation

Time complexity: O(m²)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<int> executeInstructions(int n, vector<int>& startPos, string s) {

const int m = s.length();

auto moves = [&](int k) -> int {

int x = startPos[1];

int y = startPos[0];

for (int i = k; i < m; ++i) {

switch (s[i]) {

case 'R': x += 1; break;

case 'D': y += 1; break;

case 'L': x -= 1; break;

case 'U': y -= 1; break;

}

if (x < 0 || x == n || y < 0 || y == n)

return i - k;

}

return m - k;

};

vector<int> ans(m);

for (int i = 0; i < m; ++i)

ans[i] = moves(i);

return ans;

}

};