Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins’ values.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Return the root of the modified tree.
Note that the depth of a node is the number of edges in the path from the root node to it.
Example 1:
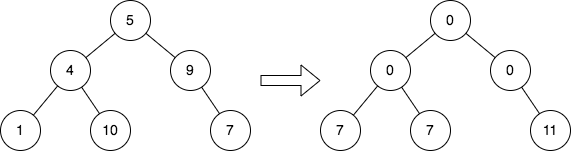
Input: root = [5,4,9,1,10,null,7] Output: [0,0,0,7,7,null,11] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 5 does not have any cousins so its sum is 0. - Node with value 4 does not have any cousins so its sum is 0. - Node with value 9 does not have any cousins so its sum is 0. - Node with value 1 has a cousin with value 7 so its sum is 7. - Node with value 10 has a cousin with value 7 so its sum is 7. - Node with value 7 has cousins with values 1 and 10 so its sum is 11.
Example 2:

Input: root = [3,1,2] Output: [0,0,0] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 3 does not have any cousins so its sum is 0. - Node with value 1 does not have any cousins so its sum is 0. - Node with value 2 does not have any cousins so its sum is 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 104
Solution: Level Order Sum
Time complexity: O(n)
Space complexity: O(n)
DFS, two passes
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
// Author: Huahua class Solution { public: TreeNode* replaceValueInTree(TreeNode* root) { unordered_map<TreeNode*, int> parentSum; parentSum[nullptr] = root->val; vector<int> levelSums; function<void(TreeNode*, int)> dfs = [&](TreeNode* node, int depth) { if (!node) return; if (levelSums.size() <= depth) { levelSums.push_back(0); } levelSums[depth] += node->val; if (node->left) { parentSum[node] += node->left->val; dfs(node->left, depth + 1); } if (node->right) { parentSum[node] += node->right->val; dfs(node->right, depth + 1); } }; function<void(TreeNode*, TreeNode*, int)> dfs2 = [&](TreeNode* node, TreeNode* p, int depth) { if (!node) return; node->val = levelSums[depth] - parentSum[p]; dfs2(node->left, node, depth + 1); dfs2(node->right, node, depth + 1); }; dfs(root, 0); dfs2(root, nullptr, 0); return root; } }; |
BFS, one+ pass
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
// Author: Huahua class Solution { public: TreeNode* replaceValueInTree(TreeNode* root) { root->val = 0; queue<TreeNode*> q({root}); while (!q.empty()) { vector<TreeNode*> nodes; int sum = 0; for (int s = q.size(); s; --s) { TreeNode* node = q.front(); q.pop(); nodes.push_back(node); if (node->left) { q.push(node->left); sum += node->left->val; } if (node->right) { q.push(node->right); sum += node->right->val; } } for (TreeNode* node : nodes) { int val = sum - (node->left ? node->left->val : 0) - (node->right ? node->right->val : 0); if (node->left) node->left->val = val; if (node->right) node->right->val = val; } } return root; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment