Run-length encoding is a string compression method that works by replacing consecutive identical characters (repeated 2 or more times) with the concatenation of the character and the number marking the count of the characters (length of the run). For example, to compress the string "aabccc" we replace "aa" by "a2" and replace "ccc" by "c3". Thus the compressed string becomes "a2bc3".
Notice that in this problem, we are not adding '1' after single characters.
Given a string s and an integer k. You need to delete at most k characters from s such that the run-length encoded version of s has minimum length.
Find the minimum length of the run-length encoded version of s after deleting at most k characters.
Example 1:
Input: s = "aaabcccd", k = 2 Output: 4 Explanation: Compressing s without deleting anything will give us "a3bc3d" of length 6. Deleting any of the characters 'a' or 'c' would at most decrease the length of the compressed string to 5, for instance delete 2 'a' then we will have s = "abcccd" which compressed is abc3d. Therefore, the optimal way is to delete 'b' and 'd', then the compressed version of s will be "a3c3" of length 4.
Example 2:
Input: s = "aabbaa", k = 2 Output: 2 Explanation: If we delete both 'b' characters, the resulting compressed string would be "a4" of length 2.
Example 3:
Input: s = "aaaaaaaaaaa", k = 0 Output: 3 Explanation: Since k is zero, we cannot delete anything. The compressed string is "a11" of length 3.
Constraints:
1 <= s.length <= 1000 <= k <= s.lengthscontains only lowercase English letters.
Solution 0: Brute Force DFS (TLE)
Time complexity: O(C(n,k))
Space complexity: O(k)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Solution { public: int getLengthOfOptimalCompression(string s, int k) { const int n = s.length(); auto encode = [&]() -> int { char p = '$'; int count = 0; int len = 0; for (char c : s) { if (c == '.') continue; if (c != p) { p = c; count = 0; } ++count; if (count <= 2 || count == 10 || count == 100) ++len; } return len; }; function<int(int, int)> dfs = [&](int start, int k) -> int { if (start == n || k == 0) return encode(); int ans = n; for (int i = start; i < n; ++i) { char c = s[i]; s[i] = '.'; // delete ans = min(ans, dfs(i + 1, k - 1)); s[i] = c; } return ans; }; return dfs(0, k); } }; |
Solution1: DP
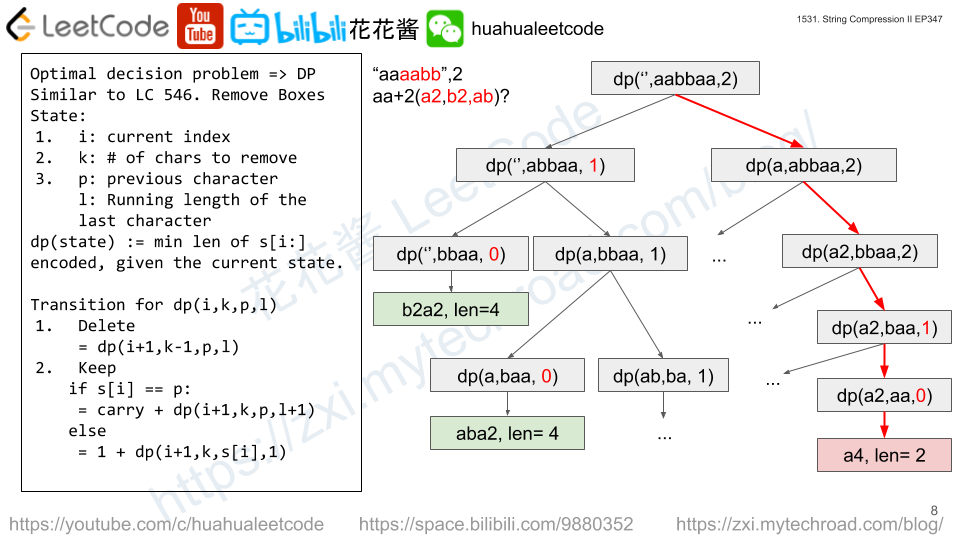
State:
i: the start index of the substring
last: last char
len: run-length
k: # of chars that can be deleted.
base case:
1. k < 0: return inf # invalid
2. i >= s.length(): return 0 # done
Transition:
1. if s[i] == last: return carry + dp(i + 1, last, len + 1, k)
2. if s[i] != last:
return min(1 + dp(i + 1, s[i], 1, k, # start a new group with s[i]
dp(i + 1, last, len, k -1) # delete / skip s[i], keep it as is.
Time complexity: O(n^3*26)
Space complexity: O(n^3*26)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
int cache[101][27][101][101]; class Solution { public: int getLengthOfOptimalCompression(string s, int k) { memset(cache, -1, sizeof(cache)); // Min length of compressioned string of s[i:] // 1. last char is |last| // 2. current run-length is len // 3. we can delete k chars. function<int(int, int, int, int)> dp = [&](int i, int last, int len, int k) { if (k < 0) return INT_MAX / 2; if (i >= s.length()) return 0; int& ans = cache[i][last][len][k]; if (ans != -1) return ans; if (s[i] - 'a' == last) { // same as the previous char, no need to delete. int carry = (len == 1 || len == 9 || len == 99); ans = carry + dp(i + 1, last, len + 1, k); } else { ans = min(1 + dp(i + 1, s[i] - 'a', 1, k), // keep s[i] dp(i + 1, last, len, k - 1)); // delete s[i] } return ans; }; return dp(0, 26, 0, k); } }; |
State compression

dp[i][k] := min len of s[i:] encoded by deleting at most k charchters.
dp[i][k] = min(dp[i+1][k-1] # delete s[i]
encode_len(s[i~j] == s[i]) + dp(j+1, k – sum(s[i~j])) for j in range(i, n)) # keep
Time complexity: O(n^2*k)
Space complexity: O(n*k)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
// Author: Huahua class Solution { public: int getLengthOfOptimalCompression(string s, int k) { const int n = s.length(); vector<vector<int>> cache(n, vector<int>(k + 1, -1)); function<int(int, int)> dp = [&](int i, int k) -> int { if (k < 0) return n; if (i + k >= n) return 0; int& ans = cache[i][k]; if (ans != -1) return ans; ans = dp(i + 1, k - 1); // delete int len = 0; int same = 0; int diff = 0; for (int j = i; j < n && diff <= k; ++j) { if (s[j] == s[i] && ++same) { if (same <= 2 || same == 10 || same == 100) ++len; } else { ++diff; } ans = min(ans, len + dp(j + 1, k - diff)); } return ans; }; return dp(0, k); } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
// Author: Huahua class Solution { private int[][] dp; private char[] s; private int n; public int getLengthOfOptimalCompression( String s, int k) { this.s = s.toCharArray(); this.n = s.length(); this.dp = new int[n][k + 1]; for (int[] row : dp) Arrays.fill(row, -1); return dp(0, k); } private int dp(int i, int k) { if (k < 0) return this.n; if (i + k >= n) return 0; // done or delete all. int ans = dp[i][k]; if (ans != -1) return ans; ans = dp(i + 1, k - 1); // delete s[i] int len = 0; int same = 0; int diff = 0; for (int j = i; j < n && diff <= k; ++j) { if (s[j] == s[i]) { ++same; if (same <= 2 || same == 10 || same == 100) ++len; } else { ++diff; } ans = Math.min(ans, len + dp(j + 1, k - diff)); } dp[i][k] = ans; return ans; } } |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# Author: Huahua class Solution: def getLengthOfOptimalCompression(self, s: str, k: int) -> int: n = len(s) @functools.lru_cache(maxsize=None) def dp(i, k): if k < 0: return n if i + k >= n: return 0 ans = dp(i + 1, k - 1) l = 0 same = 0 for j in range(i, n): if s[j] == s[i]: same += 1 if same <= 2 or same == 10 or same == 100: l += 1 diff = j - i + 1 - same if diff < 0: break ans = min(ans, l + dp(j + 1, k - diff)) return ans return dp(0, k) |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment