Problem:
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example 1:
|
1 2 3 |
[[1,3,1], [1,5,1], [4,2,1]] |
Given the above grid map, return 7. Because the path 1→3→1→1→1 minimizes the sum.
Idea:
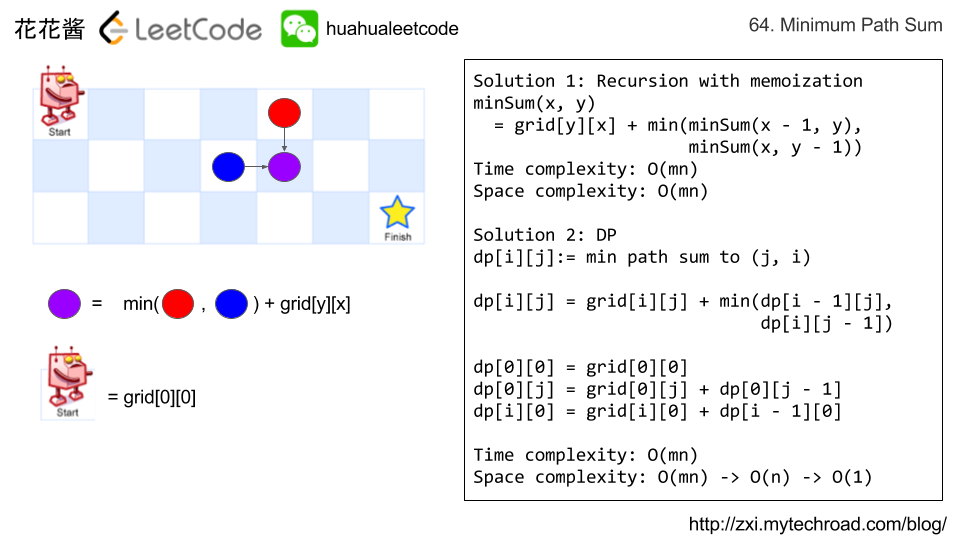
DP
Solution 1:
C++ / Recursion with memoization
Time complexity: O(mn)
Space complexity: O(mn)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
// Author: Huahua // Runtime: 9 ms class Solution { public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); if (m == 0) return 0; int n = grid[0].size(); s_ = vector<vector<int>>(m, vector<int>(n, 0)); return minPathSum(grid, n - 1, m - 1, n, m); } private: long minPathSum(const vector<vector<int>>& grid, int x, int y, int n, int m) { if (x == 0 && y == 0) return grid[y][x]; if (x < 0 || y < 0) return INT_MAX; if (s_[y][x] > 0) return s_[y][x]; int ans = grid[y][x] + min(minPathSum(grid, x - 1, y, n, m), minPathSum(grid, x, y - 1, n, m)); return s_[y][x] = ans; } vector<vector<int>> s_; }; |
Solution 2:
C++ / DP
Time complexity: O(mn)
Space complexity: O(1)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
// Author: Huahua // Runtime: 9 ms class Solution { public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); if (m == 0) return 0; int n = grid[0].size(); for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) { if (i == 0 && j == 0) continue; if (i == 0) grid[i][j] += grid[i][j - 1]; else if (j == 0) grid[i][j] += grid[i - 1][j]; else grid[i][j] += min(grid[i][j - 1], grid[i - 1][j]); } return grid[m - 1][n - 1]; } }; |
Related Problems:
请尊重作者的劳动成果，转载请注明出处！花花保留对文章／视频的所有权利。
如果您喜欢这篇文章／视频，欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.
Paypal
Venmo
huahualeetcode
huahualeetcode
微信打赏
Nice codes and explanation, Thank you Huahua.
Changes for solution 1
a)change the order of x and y. (Don’t know why you switch them:))
b) Remove unused arguments m and n.
The following codes were accepted too.
class Solution {
public:
int minPathSum(vector<vector>& grid) {
int m = grid.size();
if (m == 0) return 0;
int n = grid[0].size();
s_ = vector<vector>(m, vector(n, 0));
return minPathSum(grid, m – 1, n – 1);
}
private:
long minPathSum(const vector<vector>& grid,
int x, int y) {
if (x == 0 && y == 0) return grid[y][x];
if (x < 0 || y 0) return s_[x][y];
int ans = grid[x][y] + min(minPathSum(grid, x – 1, y),
minPathSum(grid, x, y – 1));
return s_[x][y] = ans;
}
vector<vector> s_;
};