You are given an undirected graph represented by an integer n, which is the number of nodes, and edges, where edges[i] = [ui, vi] which indicates that there is an undirected edge between ui and vi. You are also given an integer array queries.
The answer to the jth query is the number of pairs of nodes (a, b) that satisfy the following conditions:
a < bcntis strictly greater thanqueries[j], wherecntis the number of edges incident toaorb.
Return an array answers such that answers.length == queries.length and answers[j] is the answer of the jth query.
Note that there can be repeated edges.
Example 1: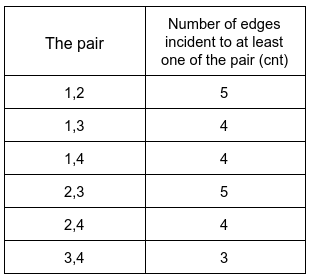
Input: n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3] Output: [6,5] Explanation: The number of edges incident to at least one of each pair is shown above.
Example 2:
Input: n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5] Output: [10,10,9,8,6]
Constraints:
2 <= n <= 2 * 1041 <= edges.length <= 1051 <= ui, vi <= nui != vi1 <= queries.length <= 200 <= queries[j] < edges.length
Solution 1: Pre-compute
Pre-compute # of pairs with total edges >= k. where k is from 0 to max_degree * 2 + 1.
Time complexity: (|node_degrees|2 + V + E)
Space complexity: O(V+E)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
// Author: huahua class Solution { public: vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) { vector<int> node_degrees(n); unordered_map<int, int> edge_freq; for (auto& e : edges) { sort(begin(e), end(e)); ++node_degrees[--e[0]]; ++node_degrees[--e[1]]; ++edge_freq[(e[0] << 16) | e[1]]; } const int max_degree = *max_element(begin(node_degrees), end(node_degrees)); // Need pad one more to handle "not found / 0" case. vector<int> counts(max_degree * 2 + 2); unordered_map<int, int> degree_count; for (int i = 0; i < n; ++i) ++degree_count[node_degrees[i]]; for (auto& [d1, c1] : degree_count) for (auto& [d2, c2] : degree_count) // Only count once if degrees are different to ensure (a < b) if (d1 < d2) counts[d1 + d2] += c1 * c2; // If degrees are the same C(n, 2) to ensure (a < b) else if (d1 == d2) counts[d1 * 2] += c1 * (c1 - 1) / 2; for (auto& [key, freq] : edge_freq) { const int u = key >> 16; const int v = key & 0xFFFF; // For a pair of (u, v) their actual edge count is // d[u] + d[v] - freq[(u, v)] instead of d[u] + d[v] counts[node_degrees[u] + node_degrees[v]] -= 1; counts[node_degrees[u] + node_degrees[v] - freq] += 1; } // counts[i] = # of pairs whose total edges >= i for (int i = counts.size() - 2; i >= 0; --i) counts[i] += counts[i + 1]; vector<int> ans; for (int q : queries) ans.push_back(counts[min(q + 1, static_cast<int>(counts.size() - 1))]); return ans; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment