Problem
Starting with an undirected graph (the “original graph”) with nodes from 0 to N-1, subdivisions are made to some of the edges.
The graph is given as follows: edges[k] is a list of integer pairs (i, j, n) such that (i, j) is an edge of the original graph,
and n is the total number of new nodes on that edge.
Then, the edge (i, j) is deleted from the original graph, n new nodes (x_1, x_2, ..., x_n) are added to the original graph,
and n+1 new edges (i, x_1), (x_1, x_2), (x_2, x_3), ..., (x_{n-1}, x_n), (x_n, j) are added to the original graph.
Now, you start at node 0 from the original graph, and in each move, you travel along one edge.
Return how many nodes you can reach in at most M moves.
Example 1:
Input: edge = [[0,1,10],[0,2,1],[1,2,2]], M = 6, N = 3 Output: 13 Explanation: The nodes that are reachable in the final graph after M = 6 moves are indicated below.
Example 2:
Input: edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], M = 10, N = 4 Output: 23
Note:
0 <= edges.length <= 100000 <= edges[i][0] < edges[i][1] < N- There does not exist any
i != jfor whichedges[i][0] == edges[j][0]andedges[i][1] == edges[j][1]. - The original graph has no parallel edges.
0 <= edges[i][2] <= 100000 <= M <= 10^91 <= N <= 3000
Solution: Dijkstra Shortest Path
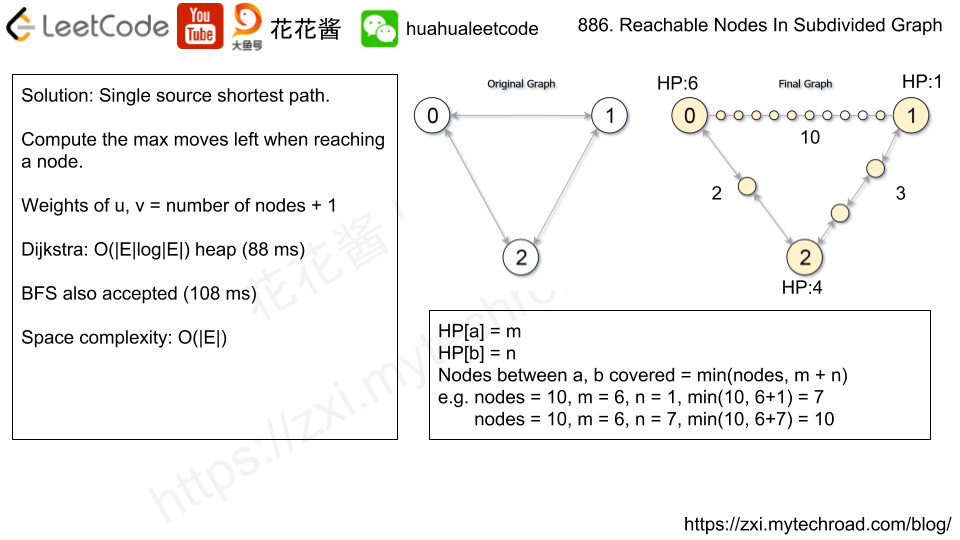
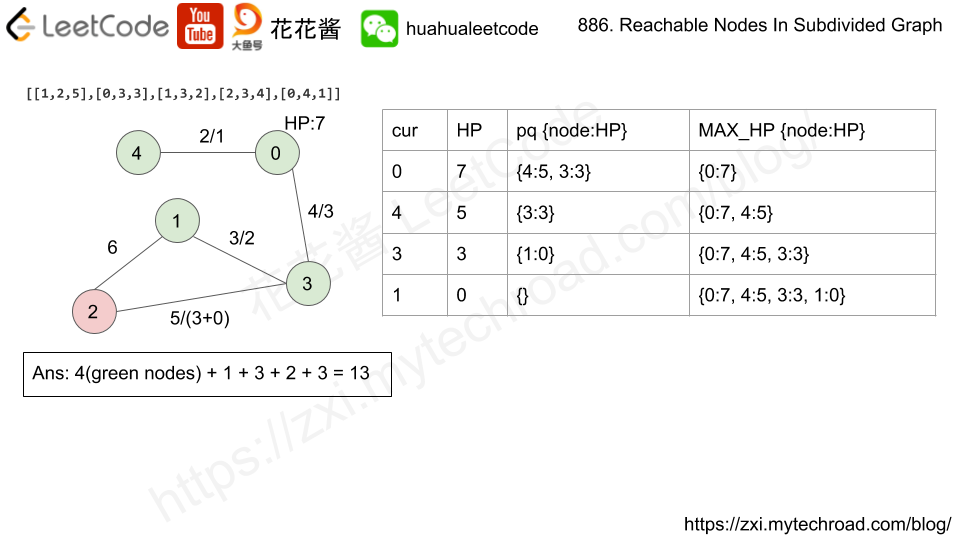
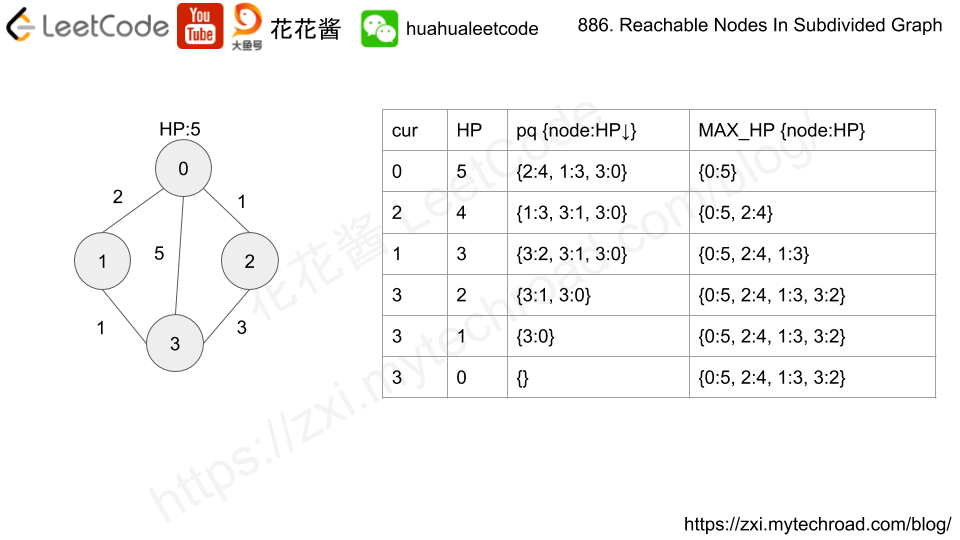
Compute the shortest from 0 to rest of the nodes. Use HP to mark the maximum moves left to reach each node.
HP[u] = a, HP[v] = b, new_nodes[u][v] = c
nodes covered between a<->b = min(c, a + b)
Time complexity: O(ElogE)
Space complexity: O(E)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
// Author: Huahua // Running time: 88 ms class Solution { public: int reachableNodes(vector<vector<int>>& edges, int M, int N) { unordered_map<int, unordered_map<int, int>> g; for (const auto& e : edges) g[e[0]][e[1]] = g[e[1]][e[0]] = e[2]; priority_queue<pair<int, int>> q; // {hp, node}, sort by HP desc unordered_map<int, int> HP; // node -> max HP left q.push({M, 0}); while (!q.empty()) { int hp = q.top().first; int cur = q.top().second; q.pop(); if (HP.count(cur)) continue; HP[cur] = hp; for (const auto& pair : g[cur]) { int nxt = pair.first; int nxt_hp = hp - pair.second - 1; if (HP.count(nxt) || nxt_hp < 0) continue; q.push({nxt_hp, nxt}); } } int ans = HP.size(); // Original nodes covered. for (const auto& e : edges) { int uv = HP.count(e[0]) ? HP[e[0]] : 0; int vu = HP.count(e[1]) ? HP[e[1]] : 0; ans += min(e[2], uv + vu); } return ans; } }; |
Optimized Dijkstra (replace hashmap with vector)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
// Author: Huahua // Running time: 56 ms (beats 88%) class Solution { public: int reachableNodes(vector<vector<int>>& edges, int M, int N) { vector<vector<pair<int, int>>> g(N); for (const auto& e : edges) { g[e[0]].emplace_back(e[1], e[2]); g[e[1]].emplace_back(e[0], e[2]); } set<pair<int, int>> q; // {hp, node}, sort by HP asc vector<int> HP(N, INT_MIN); // node -> HP left q.insert({M, 0}); int ans = 0; while (!q.empty()) { auto last_it = prev(end(q)); int hp = last_it->first; int cur = last_it->second; q.erase(last_it); if (HP[cur] != INT_MIN) continue; HP[cur] = hp; ++ans; for (const auto& pair : g[cur]) { int nxt = pair.first; int nxt_hp = hp - pair.second - 1; if (nxt_hp < 0 || HP[nxt] != INT_MIN) continue; q.insert({nxt_hp, nxt}); } } for (const auto& e : edges) { const int uv = HP[e[0]] == INT_MIN ? 0 : HP[e[0]]; const int vu = HP[e[1]] == INT_MIN ? 0 : HP[e[1]]; ans += min(e[2], uv + vu); } return ans; } }; |
Using SPFA
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
// Author: Huahua // Running time: 56 ms (beats 88%) class Solution { public: int reachableNodes(vector<vector<int>>& edges, int M, int N) { vector<vector<pair<int, int>>> g(N); for (const auto& e : edges) { g[e[0]].emplace_back(e[1], e[2]); g[e[1]].emplace_back(e[0], e[2]); } queue<int> q; vector<int> HP(N, INT_MIN); vector<bool> in_q(N); HP[0] = M; q.push(0); in_q[0] = true; // SPFA (Shortest Path Faster Algorithm). while (!q.empty()) { int u = q.front(); q.pop(); in_q[u] = false; for (const auto& pair : g[u]) { int v = pair.first; int new_hp = HP[u] - pair.second - 1; if (new_hp < 0 || new_hp <= HP[v]) continue; HP[v] = new_hp; if (in_q[v]) continue; q.push(v); in_q[v] = true; } } int ans = 0; for (int i = 0; i < N; ++i) ans += HP[i] >= 0; for (const auto& e : edges) { const int uv = HP[e[0]] == INT_MIN ? 0 : HP[e[0]]; const int vu = HP[e[1]] == INT_MIN ? 0 : HP[e[1]]; ans += min(e[2], uv + vu); } return ans; } }; |
BFS
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
// Author: Huahua // Running time: 108 ms class Solution { public: int reachableNodes(vector<vector<int>>& edges, int M, int N) { unordered_map<int, unordered_map<int, int>> g; for (const auto& e : edges) g[e[0]][e[1]] = g[e[1]][e[0]] = e[2]; queue<pair<int, int>> q; // {hp, node} unordered_map<int, int> HP; // node -> max HP left q.push({M, 0}); while (!q.empty()) { int hp = q.front().first; int cur = q.front().second; q.pop(); if (HP.count(cur) && HP[cur] > hp) continue; HP[cur] = hp; for (const auto& pair : g[cur]) { int nxt = pair.first; int nxt_hp = hp - pair.second - 1; if (nxt_hp < 0 || (HP.count(nxt) && HP[nxt] > nxt_hp)) continue; q.push({nxt_hp, nxt}); } } int ans = HP.size(); // Original nodes covered. for (const auto& e : edges) { int uv = HP.count(e[0]) ? HP[e[0]] : 0; int vu = HP.count(e[1]) ? HP[e[1]] : 0; ans += min(e[2], uv + vu); } return ans; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.




Be First to Comment