花花酱 LeetCode 1386. Cinema Seat Allocation

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i]=[3,8] means the seat located in row 3 and labelled with 8 is already reserved. 

Return the maximum number of four-person families you can allocate on the cinema seats. A four-person family occupies fours seats in one row, that are next to each other. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be next to each other, however, It is permissible for the four-person family to be separated by an aisle, but in that case, exactly two people have to sit on each side of the aisle.

Example 1:

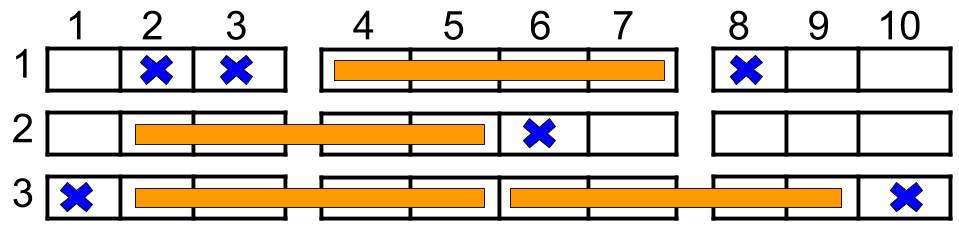
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four families, where seats mark with blue are already reserved and contiguous seats mark with orange are for one family. 

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

Constraints:

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

Solution: HashTable + Greedy

if both seat[2~5] seat[6~9] are empty, seat two groups.
if any of seat[2~5] seat[4~7] seat[6~9] is empty seat one group.
if there is no one sit in a row, seat two groups.

Time complexity: O(|reservedSeats|)
Space complexity: O(|rows|)