We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with speed 1 unit per second. Some of the ants move to the left, the other move to the right.
When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions doesn’t take any additional time.
When an ant reaches one end of the plank at a time t, it falls out of the plank imediately.
Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right. Return the moment when the last ant(s) fall out of the plank.
Example 1:
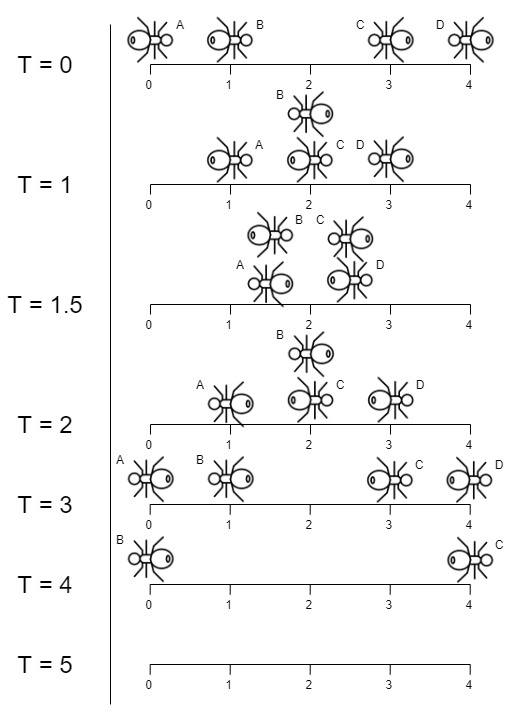
Input: n = 4, left = [4,3], right = [0,1] Output: 4 Explanation: In the image above: -The ant at index 0 is named A and going to the right. -The ant at index 1 is named B and going to the right. -The ant at index 3 is named C and going to the left. -The ant at index 4 is named D and going to the left. Note that the last moment when an ant was on the plank is t = 4 second, after that it falls imediately out of the plank. (i.e. We can say that at t = 4.0000000001, there is no ants on the plank).
Example 2:

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7] Output: 7 Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
Example 3:

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = [] Output: 7 Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
Example 4:
Input: n = 9, left = [5], right = [4] Output: 5 Explanation: At t = 1 second, both ants will be at the same intial position but with different direction.
Example 5:
Input: n = 6, left = [6], right = [0] Output: 6
Constraints:
1 <= n <= 10^40 <= left.length <= n + 10 <= left[i] <= n0 <= right.length <= n + 10 <= right[i] <= n1 <= left.length + right.length <= n + 1- All values of
leftandrightare unique, and each value can appear only in one of the two arrays.
Solution: Keep Walking
When two ants A –> and <– B meet at some point, they change directions <– A B –>, we can swap the ids of the ants as <– B A–>, so it’s the same as walking individually and passed by. Then we just need to find the max/min of the left/right arrays.
Time complexity: O(n)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 |
// Author: Huahua class Solution { public: int getLastMoment(int n, vector<int>& left, vector<int>& right) { const int t1 = left.empty() ? 0 : *max_element(cbegin(left), cend(left)); const int t2 = right.empty() ? 0 : n - *min_element(cbegin(right), cend(right)); return max(t1, t2); } }; |
Java
|
1 2 3 4 5 6 7 8 |
// Author: Huahua class Solution { public int getLastMoment(int n, int[] left, int[] right) { int t1 = left.length == 0 ? 0 : Arrays.stream(left).max().getAsInt(); int t2 = right.length == 0 ? 0 : n - Arrays.stream(right).min().getAsInt(); return Math.max(t1, t2); } } |
Python3
|
1 2 3 4 5 6 |
# Author: Huahua class Solution: def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int: t1 = max(left) if left else 0 t2 = n - min(right) if right else 0 return max(t1, t2) |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment