Huahua’s Tech Road

花花酱 LeetCode 1711. Count Good Meals

By zxi on January 2, 2021

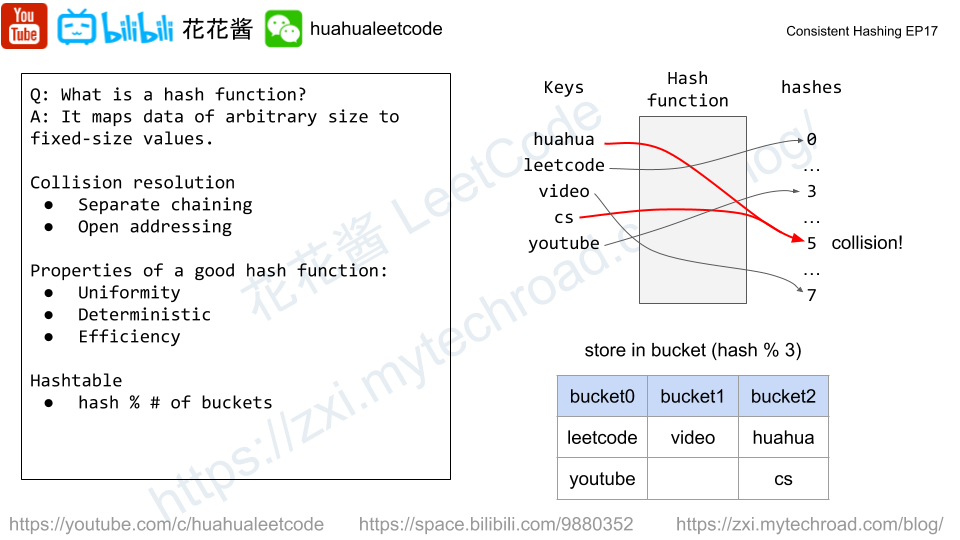
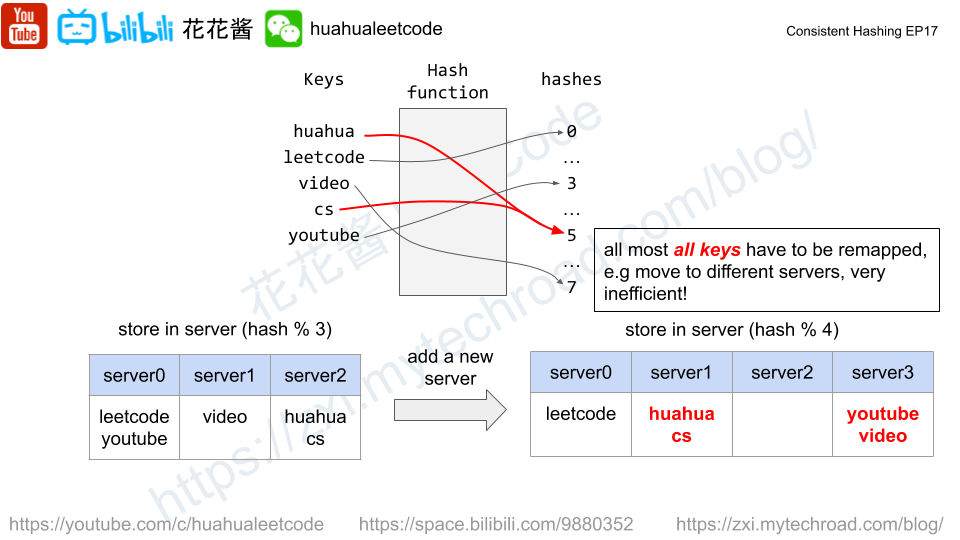
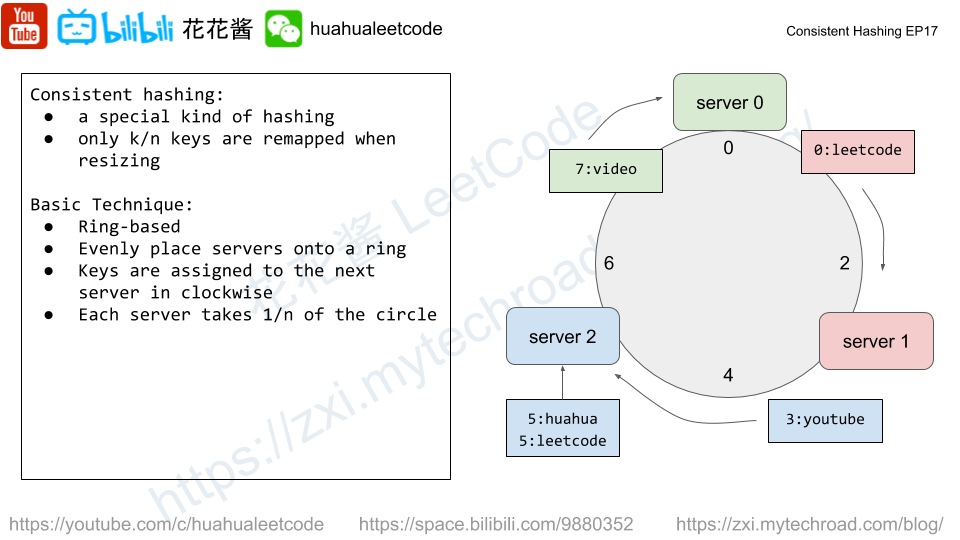
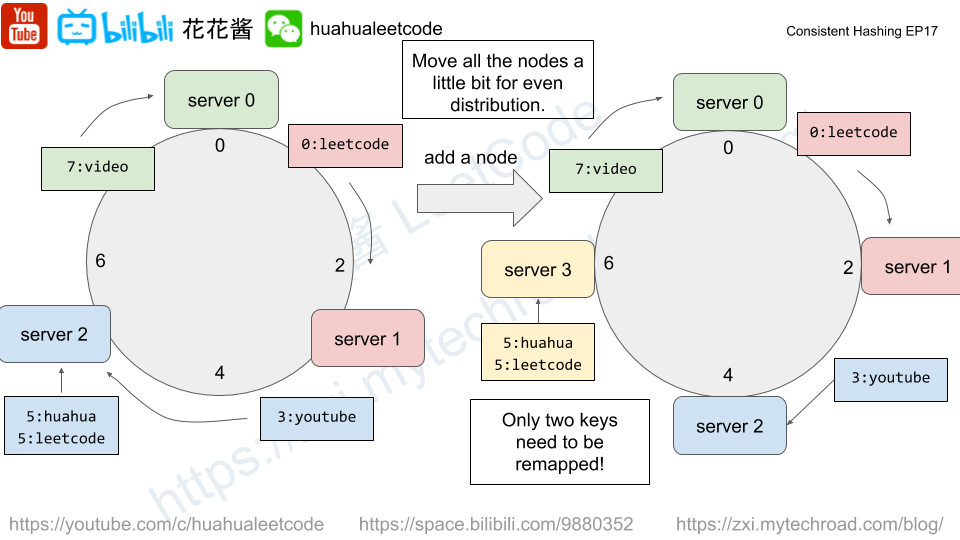
A good meal is a meal that contains exactly two different food items with a sum of deliciousness equal to a power of two.

You can pick any two different foods to make a good meal.

Given an array of integers deliciousness where deliciousness[i] is the deliciousness of the i^th item of food, return the number of different good meals you can make from this list modulo 10⁹ + 7.

Note that items with different indices are considered different even if they have the same deliciousness value.

Example 1:

Input: deliciousness = [1,3,5,7,9]
Output: 4
Explanation: The good meals are (1,3), (1,7), (3,5) and, (7,9).
Their respective sums are 4, 8, 8, and 16, all of which are powers of 2.

Example 2:

Input: deliciousness = [1,1,1,3,3,3,7]
Output: 15
Explanation: The good meals are (1,1) with 3 ways, (1,3) with 9 ways, and (1,7) with 3 ways.

Constraints:

1 <= deliciousness.length <= 10⁵
0 <= deliciousness[i] <= 2²⁰

Solution: Hashtable

Same idea as LeetCode 1: Two Sum

Use a hashtable to store the occurrences of all the numbers added so far. For a new number x, check all possible 2^i – x. ans += freq[2^i – x] 0 <= i <= 21

Time complexity: O(22n)
Space complexity: O(n)

C++

class Solution {

public:

int countPairs(vector<int>& A) {

constexpr int kMod = 1e9 + 7;

unordered_map<int, int> m;

long ans = 0;

for (int x : A) {

for (int t = 1; t <= 1 << 21; t *= 2) {

auto it = m.find(t - x);

if (it != end(m)) ans += it->second;

}

++m[x];

}

return ans % kMod;

}

};

Python3

class Solution:

def countPairs(self, deliciousness: List[int]) -> int:

sums = [1<<i for i in range(22)]

m = defaultdict(int)

ans = 0

for x in deliciousness:

for t in sums:

if t - x in m: ans += m[t - x]

m[x] += 1

return ans % (10**9 + 7)

花花酱 LeetCode 1710. Maximum Units on a Truck

By zxi on January 2, 2021

You are assigned to put some amount of boxes onto one truck. You are given a 2D array boxTypes, where boxTypes[i] = [numberOfBoxes_i, numberOfUnitsPerBox_i]:

numberOfBoxes_i is the number of boxes of type i.
numberOfUnitsPerBox_iis the number of units in each box of the type i.

You are also given an integer truckSize, which is the maximum number of boxes that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed truckSize.

Return the maximum total number of units that can be put on the truck.

Example 1:

Input: boxTypes = [[1,3],[2,2],[3,1]], truckSize = 4
Output: 8
Explanation: There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 * 3) + (2 * 2) + (1 * 1) = 8.

Example 2:

Input: boxTypes = [[5,10],[2,5],[4,7],[3,9]], truckSize = 10
Output: 91

Constraints:

1 <= boxTypes.length <= 1000
1 <= numberOfBoxes_i, numberOfUnitsPerBox_i <= 1000
1 <= truckSize <= 10⁶

Solution: Greedy

Sort by unit in descending order.

Time complexity: O(nlogn)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int maximumUnits(vector<vector<int>>& boxTypes, int truckSize) {

sort(begin(boxTypes), end(boxTypes), [](const auto& a, const auto& b){

return a[1] > b[1]; // Sort by unit DESC

});

int ans = 0;

for (const auto& b : boxTypes) {

ans += b[1] * min(b[0], truckSize);

if ((truckSize -= b[0]) <= 0) break;

}

return ans;

}

};

Consistent Hashing

By zxi on December 30, 2020

花花酱 LeetCode 1707. Maximum XOR With an Element From Array

By zxi on December 27, 2020

You are given an array nums consisting of non-negative integers. You are also given a queries array, where queries[i] = [x_i, m_i].

The answer to the i^th query is the maximum bitwise XOR value of x_i and any element of nums that does not exceed m_i. In other words, the answer is max(nums[j] XOR x_i) for all j such that nums[j] <= m_i. If all elements in nums are larger than m_i, then the answer is -1.

Return an integer array answer where answer.length == queries.length and answer[i] is the answer to the i^th query.

Example 1:

Input: nums = [0,1,2,3,4], queries = [[3,1],[1,3],[5,6]]
Output: [3,3,7]
Explanation:
1) 0 and 1 are the only two integers not greater than 1. 0 XOR 3 = 3 and 1 XOR 3 = 2. The larger of the two is 3.
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.

Example 2:

Input: nums = [5,2,4,6,6,3], queries = [[12,4],[8,1],[6,3]]
Output: [15,-1,5]

Constraints:

1 <= nums.length, queries.length <= 10⁵
queries[i].length == 2
0 <= nums[j], x_i, m_i <= 10⁹

Solution: Trie on the fly

We can build the trie on the fly by sorting nums in ascending order and queries by its limit, insert nums into the trie up the limit.

Time complexity: O(nlogn + QlogQ)
Space complexity: O(n)

C++

// Author: Huahua

class Trie {

public:

Trie(): children{nullptr, nullptr} {}

Trie* children[2];

};

class Solution {

public:

vector<int> maximizeXor(vector<int>& nums, vector<vector<int>>& queries) {

const int n = nums.size();

sort(begin(nums), end(nums));

const int Q = queries.size();

for (int i = 0; i < Q; ++i)

queries[i].push_back(i);

sort(begin(queries), end(queries), [](const auto& q1, const auto& q2) {

return q1[1] < q2[1];

});

Trie root;

auto insert = [&](int num) {

Trie* node = &root;

for (int i = 31; i >= 0; --i) {

int bit = (num >> i) & 1;

if (!node->children[bit])

node->children[bit] = new Trie();

node = node->children[bit];

}

};

auto query = [&](int num) {

Trie* node = &root;

int sum = 0;

for (int i = 31; i >= 0; --i) {

if (!node) return -1;

int bit = (num >> i) & 1;

if (node->children[1 - bit]) {

sum |= (1 << i);

node = node->children[1 - bit];

} else {

node = node->children[bit];

}

return sum;

};

vector<int> ans(Q);

int i = 0;

for (const auto& q : queries) {

while (i < n && nums[i] <= q[1]) insert(nums[i++]);

ans[q[2]] = query(q[0]);

}

return ans;

}

};

花花酱 LeetCode 421. Maximum XOR of Two Numbers in an Array

By zxi on December 27, 2020

Given an integer array nums, return the maximum result of nums[i] XOR nums[j], where 0 ≤ i ≤ j < n.

Follow up: Could you do this in O(n) runtime?

Example 1:

Input: nums = [3,10,5,25,2,8]
Output: 28
Explanation: The maximum result is 5 XOR 25 = 28.

Example 2:

Input: nums = [0]
Output: 0

Example 3:

Input: nums = [2,4]
Output: 6

Example 4:

Input: nums = [8,10,2]
Output: 10

Example 5:

Input: nums = [14,70,53,83,49,91,36,80,92,51,66,70]
Output: 127

Constraints:

1 <= nums.length <= 2 * 10⁴
0 <= nums[i] <= 2³¹ - 1

Solution: Trie

Time complexity: O(31*2*n)
Space complexity: O(31*2*n)

C++

// Author: Huahua

class Trie {

public:

Trie(): children(2) {}

vector<unique_ptr<Trie>> children;

};

class Solution {

public:

int findMaximumXOR(vector<int>& nums) {

Trie root;

// Insert a number into the trie.

auto insert = [&](Trie* node, int num) {

for (int i = 31; i >= 0; --i) {

int bit = (num >> i) & 1;

if (!node->children[bit])

node->children[bit] = std::make_unique<Trie>();

node = node->children[bit].get();

}

};

// Find max xor sum of num and another element in the array.

auto query = [&](Trie* node, int num) {

int sum = 0;

for (int i = 31; i >= 0; --i) {

int bit = (num >> i) & 1;

if (node->children[1 - bit]) {

sum += (1 << i);

node = node->children[1 - bit].get();

} else {

node = node->children[bit].get();

}

return sum;

};

// Insert all numbers.

for (int x : nums)

insert(&root, x);

int ans = 0;

// For each number find the maximum xor sum.

for (int x : nums)

ans = max(ans, query(&root, x));

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1711. Count Good Meals

Solution: Hashtable

C++

Python3

花花酱 LeetCode 1710. Maximum Units on a Truck

Solution: Greedy

C++

Consistent Hashing

花花酱 LeetCode 1707. Maximum XOR With an Element From Array

Solution: Trie on the fly

C++

花花酱 LeetCode 421. Maximum XOR of Two Numbers in an Array

Solution: Trie

C++