Huahua’s Tech Road

花花酱 LeetCode 1670. Design Front Middle Back Queue

By zxi on November 28, 2020

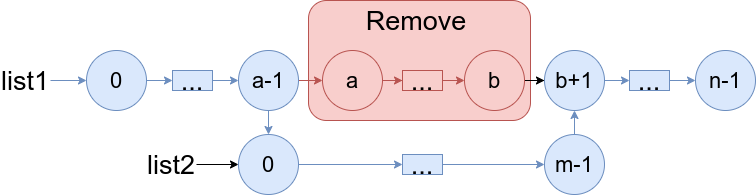
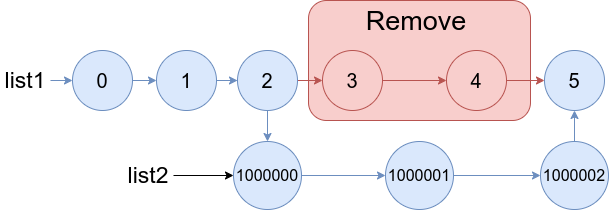
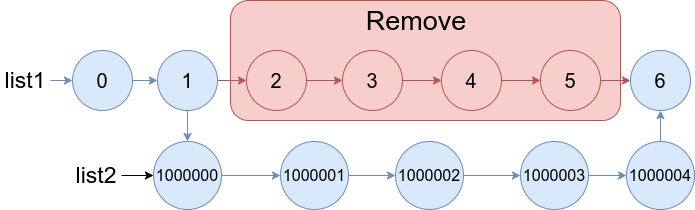
Design a queue that supports push and pop operations in the front, middle, and back.

Implement the FrontMiddleBack class:

FrontMiddleBack() Initializes the queue.
void pushFront(int val) Adds val to the front of the queue.
void pushMiddle(int val) Adds val to the middle of the queue.
void pushBack(int val) Adds val to the back of the queue.
int popFront() Removes the front element of the queue and returns it. If the queue is empty, return -1.
int popMiddle() Removes the middle element of the queue and returns it. If the queue is empty, return -1.
int popBack() Removes the back element of the queue and returns it. If the queue is empty, return -1.

Notice that when there are two middle position choices, the operation is performed on the frontmost middle position choice. For example:

Pushing 6 into the middle of [1, 2, 3, 4, 5] results in [1, 2, 6, 3, 4, 5].
Popping the middle from [1, 2, 3, 4, 5, 6] returns 3 and results in [1, 2, 4, 5, 6].

Example 1:

Input:
["FrontMiddleBackQueue", "pushFront", "pushBack", "pushMiddle", "pushMiddle", "popFront", "popMiddle", "popMiddle", "popBack", "popFront"]
[[], [1], [2], [3], [4], [], [], [], [], []]
Output:
[null, null, null, null, null, 1, 3, 4, 2, -1]
Explanation:
FrontMiddleBackQueue q = new FrontMiddleBackQueue();
q.pushFront(1);   // [1]
q.pushBack(2);    // [1, 2]
q.pushMiddle(3);  // [1, 3, 2]
q.pushMiddle(4);  // [1, 4, 3, 2]
q.popFront();     // return 1 -> [4, 3, 2]
q.popMiddle();    // return 3 -> [4, 2]
q.popMiddle();    // return 4 -> [2]
q.popBack();      // return 2 -> []
q.popFront();     // return -1 -> [] (The queue is empty)

Constraints:

1 <= val <= 10⁹
At most 1000 calls will be made to pushFront, pushMiddle, pushBack, popFront, popMiddle, and popBack.

Solution: List + Middle Iterator

Time complexity: O(1) per op
Space complexity: O(n) in total

C++

// Author: Huahua

class FrontMiddleBackQueue {

public:

FrontMiddleBackQueue() {}

void pushFront(int val) {

q_.push_front(val);

updateMit(even() ? -1 : 0);

}

void pushMiddle(int val) {

if (q_.empty())

q_.push_back(val);

else

q_.insert(even() ? next(mit_) : mit_, val);

updateMit(even() ? -1 : 1);

}

void pushBack(int val) {

q_.push_back(val);

updateMit(even() ? 0 : 1);

}

int popFront() {

if (q_.empty()) return -1;

int val = q_.front();

q_.pop_front();

updateMit(even() ? 0 : 1);

return val;

}

int popMiddle() {

if (q_.empty()) return -1;

int val = *mit_;

mit_ = q_.erase(mit_);

updateMit(even() ? -1 : 0);

return val;

}

int popBack() {

if (q_.empty()) return -1;

int val = q_.back();

q_.pop_back();

updateMit(even() ? -1 : 0);

return val;

}

private:

void updateMit(int delta) {

if (q_.size() <= 1) {

mit_ = begin(q_);

} else {

if (delta > 0) ++mit_;

if (delta < 0) --mit_;

}

bool even() const { return q_.size() % 2 == 0; }

list<int> q_;

list<int>::iterator mit_;

};

花花酱 LeetCode 1668. Maximum Repeating Substring

By zxi on November 28, 2020

For a string sequence, a string word is k-repeating if word concatenated k times is a substring of sequence. The word‘s maximum k-repeating value is the highest value k where word is k-repeating in sequence. If word is not a substring of sequence, word‘s maximum k-repeating value is 0.

Given strings sequence and word, return the maximum k-repeating value of word in sequence.

Example 1:

Input: sequence = "ababc", word = "ab"
Output: 2
Explanation: "abab" is a substring in "ababc".

Example 2:

Input: sequence = "ababc", word = "ba"
Output: 1
Explanation: "ba" is a substring in "ababc". "baba" is not a substring in "ababc".

Example 3:

Input: sequence = "ababc", word = "ac"
Output: 0
Explanation: "ac" is not a substring in "ababc".

Constraints:

1 <= sequence.length <= 100
1 <= word.length <= 100
sequence and word contains only lowercase English letters.

Solution: Brute Force

Time complexity: O(n^2)
Space complexity: O(n)

C++

class Solution {

public:

int maxRepeating(string sequence, string word) {

string s(word);

for (int i = 1;;++i) {

if (sequence.find(s) == string::npos) return i - 1;

s += word;

}

return -1;

}

};

花花酱 LeetCode 1659. Maximize Grid Happiness

By zxi on November 22, 2020

You are given four integers, m, n, introvertsCount, and extrovertsCount. You have an m x n grid, and there are two types of people: introverts and extroverts. There are introvertsCount introverts and extrovertsCount extroverts.

You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you do not have to have all the people living in the grid.

The happiness of each person is calculated as follows:

Introverts start with 120 happiness and lose 30 happiness for each neighbor (introvert or extrovert).
Extroverts start with 40 happiness and gain 20 happiness for each neighbor (introvert or extrovert).

Neighbors live in the directly adjacent cells north, east, south, and west of a person’s cell.

The grid happiness is the sum of each person’s happiness. Return the maximum possible grid happiness.

Example 1:

Input: m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
Output: 240
Explanation: Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 * 30) (0 neighbors) = 120
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
The grid happiness is 120 + 60 + 60 = 240.
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.

Example 2:

Input: m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
Output: 260
Explanation: Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 * 20) (2 neighbors) = 80
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
The grid happiness is 90 + 80 + 90 = 260.

Example 3:

Input: m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
Output: 240

Constraints:

1 <= m, n <= 5
0 <= introvertsCount, extrovertsCount <= min(m * n, 6)

Solution: DP

dp(x, y, in, ex, mask) := max score at (x, y) with in and ex left and the state of previous row is mask.

Mask is ternary, mask(i) = {0, 1, 2} means {empty, in, ex}, there are at most 3^n = 3^5 = 243 different states.

Total states / Space complexity: O(m*n*3^n*in*ex) = 5*5*3^5*6*6
Space complexity: O(m*n*3^n*in*ex)

C++

class Solution {

public:

int getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount) {

constexpr int kMaxStates = 243;

int dp[6][6][7][7][kMaxStates];

memset(dp, -1, sizeof(dp));

auto get = [](int val, int i) { return val / static_cast<int>(pow(3, i)) % 3; };

auto update = [](int val, int s) { return (val * 3 + s) % kMaxStates; };

vector<int> init{0, 120, 40};

vector<int> gain{0, -30, 20};

function<int(int,int,int,int,int)> dfs = [&](int x, int y, int in, int ex, int mask) {

if (in == 0 && ex == 0) return 0; // Nothing left.

if (x == n) { x = 0; ++y; }

if (y == m) return 0; // Done.

int& ans = dp[x][y][in][ex][mask];

if (ans != -1) return ans;

ans = dfs(x + 1, y, in, ex, update(mask, 0)); // Skip current cell.

vector<int> counts{0, in, ex};

int up = get(mask, n - 1);

int left = get(mask, 0);

for (int i = 1; i <= 2; ++i) {

if (counts[i] == 0) continue;

int s = init[i];

if (y - 1 >= 0 && up) s += gain[i] + gain[up];

if (x - 1 >= 0 && left) s += gain[i] + gain[left];

ans = max(ans, s + dfs(x + 1, y, in - (i==1), ex - (i==2), update(mask, i)));

}

return ans;

};

return dfs(0, 0, introvertsCount, extrovertsCount, 0);

}

};

Python3

# Author: Huahua

class Solution:

def getMaxGridHappiness(self, m: int, n: int, I: int, E: int) -> int:

init, gain = [None, 120, 40], [None, -30, 20]

get = lambda val, i: (val // (3 ** i)) % 3

update = lambda val, s: (val * 3 + s) % (3 ** n)

@lru_cache(None)

def dp(x: int, y: int, i: int, e: int, mask: int) -> int:

if x == n: x, y = 0, y + 1

if i + e == 0 or y == m: return 0

ans = dp(x + 1, y, i, e, update(mask, 0))

up, left = get(mask, n - 1), get(mask, 0)

for cur, count in enumerate([i, e], 1):

if count == 0: continue

s = init[cur]

if x - 1 >= 0 and left: s += gain[cur] + gain[left]

if y - 1 >= 0 and up: s += gain[cur] + gain[up]

ans = max(ans, s + dp(x + 1, y,

i - (cur == 1),

e - (cur == 2),

update(mask, cur)))

return ans

return dp(0, 0, I, E, 0)

花花酱 LeetCode 1665. Minimum Initial Energy to Finish Tasks

By zxi on November 22, 2020

You are given an array tasks where tasks[i] = [actual_i, minimum_i]:

actual_i is the actual amount of energy you spend to finish the i^th task.
minimum_i is the minimum amount of energy you require to begin the i^th task.

For example, if the task is [10, 12] and your current energy is 11, you cannot start this task. However, if your current energy is 13, you can complete this task, and your energy will be 3 after finishing it.

You can finish the tasks in any order you like.

Return the minimum initial amount of energy you will need to finish all the tasks.

Example 1:

Input: tasks = [[1,2],[2,4],[4,8]]
Output: 8
Explanation:
Starting with 8 energy, we finish the tasks in the following order:
    - 3rd task. Now energy = 8 - 4 = 4.
    - 2nd task. Now energy = 4 - 2 = 2.
    - 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.

Example 2:

Input: tasks = [[1,3],[2,4],[10,11],[10,12],[8,9]]
Output: 32
Explanation:
Starting with 32 energy, we finish the tasks in the following order:
    - 1st task. Now energy = 32 - 1 = 31.
    - 2nd task. Now energy = 31 - 2 = 29.
    - 3rd task. Now energy = 29 - 10 = 19.
    - 4th task. Now energy = 19 - 10 = 9.
    - 5th task. Now energy = 9 - 8 = 1.

Example 3:

Input: tasks = [[1,7],[2,8],[3,9],[4,10],[5,11],[6,12]]
Output: 27
Explanation:
Starting with 27 energy, we finish the tasks in the following order:
    - 5th task. Now energy = 27 - 5 = 22.
    - 2nd task. Now energy = 22 - 2 = 20.
    - 3rd task. Now energy = 20 - 3 = 17.
    - 1st task. Now energy = 17 - 1 = 16.
    - 4th task. Now energy = 16 - 4 = 12.
    - 6th task. Now energy = 12 - 6 = 6.

Constraints:

1 <= tasks.length <= 10⁵
1 <= actual_i <= minimum_i <= 10⁴

Solution: Greedy + Binary Search

Sort tasks by actual – min in ascending order, this will be the order we finish those tasks. Use binary search to check whether a given initial energy works or not. Note, the binary search part is unnecessary.

Time complexity: O(nlogn + nlogk)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minimumEffort(vector<vector<int>>& tasks) {

sort(begin(tasks), end(tasks), [](const auto& t1, const auto& t2) {

return t1[0] - t1[1] < t2[0] - t2[1];

});

int l = tasks[0][1], r = INT_MAX - 1;

auto check = [&](int cur) {

for (const auto& task : tasks) {

if (task[1] > cur) return false;

cur -= task[0];

}

return true;

};

while (l < r) {

const int m = l + (r - l) / 2;

check(m) ? r = m : l = m + 1;

}

return l;

}

};

Huahua's Tech Road

花花酱 LeetCode 1670. Design Front Middle Back Queue

Solution: List + Middle Iterator

C++

花花酱 LeetCode 1669. Merge In Between Linked Lists

Solution: List Operations

C++

花花酱 LeetCode 1668. Maximum Repeating Substring

Solution: Brute Force

C++

花花酱 LeetCode 1659. Maximize Grid Happiness

Solution: DP

C++

Python3

花花酱 LeetCode 1665. Minimum Initial Energy to Finish Tasks

Solution: Greedy + Binary Search

C++