Huahua’s Tech Road

花花酱 LeetCode 1642. Furthest Building You Can Reach

By zxi on November 1, 2020

You are given an integer array heights representing the heights of buildings, some bricks, and some ladders.

You start your journey from building 0 and move to the next building by possibly using bricks or ladders.

While moving from building i to building i+1 (0-indexed),

If the current building’s height is greater than or equal to the next building’s height, you do not need a ladder or bricks.
If the current building’s height is less than the next building’s height, you can either use one ladder or (h[i+1] - h[i]) bricks.

Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally.

Example 1:

Input: heights = [4,2,7,6,9,14,12], bricks = 5, ladders = 1
Output: 4
Explanation: Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.

Example 2:

Input: heights = [4,12,2,7,3,18,20,3,19], bricks = 10, ladders = 2
Output: 7

Example 3:

Input: heights = [14,3,19,3], bricks = 17, ladders = 0
Output: 3

Constraints:

1 <= heights.length <= 10⁵
1 <= heights[i] <= 10⁶
0 <= bricks <= 10⁹
0 <= ladders <= heights.length

Solution 0: DFS

Time complexity: O(2^n)
Space complexity: O(n)

AC but should be TLE

Solution 1: Binary Search + Greedy

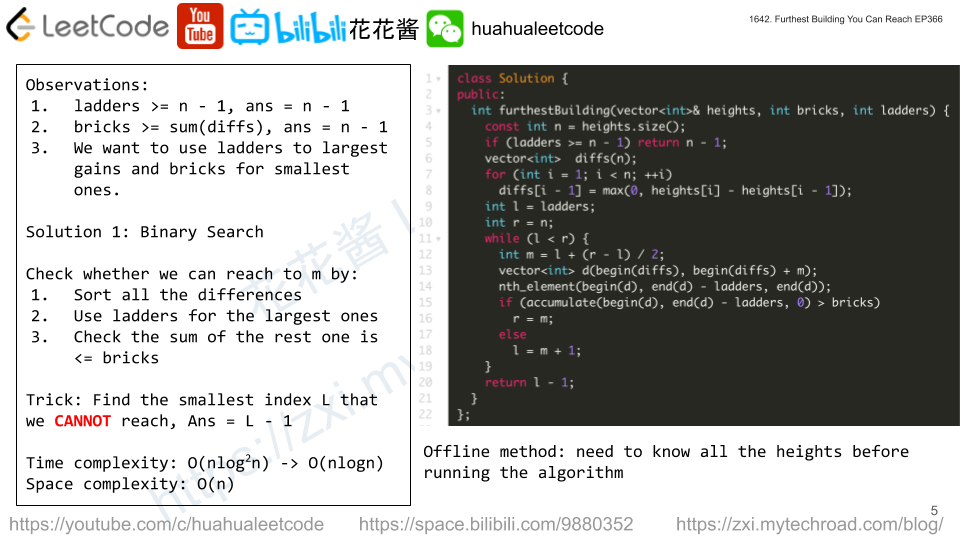
Guess we can reach to m, sort the height differences from 0~m. Use ladders for larger values and use bricks for smallest values left.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua, 300 ms

class Solution {

public:

int furthestBuilding(vector<int>& heights, int bricks, int ladders) {

const int n = heights.size();

if (ladders >= n - 1) return n - 1;

vector<int> diffs(n);

for (int i = 1; i < n; ++i)

diffs[i - 1] = max(0, heights[i] - heights[i - 1]);

int l = ladders;

int r = n;

while (l < r) {

int m = l + (r - l) / 2;

vector<int> d(begin(diffs), begin(diffs) + m);

nth_element(begin(d), end(d) - ladders, end(d));

if (accumulate(begin(d), end(d) - ladders, 0) > bricks)

r = m;

else

l = m + 1;

}

return l - 1;

}

};

Solution 2: Min heap

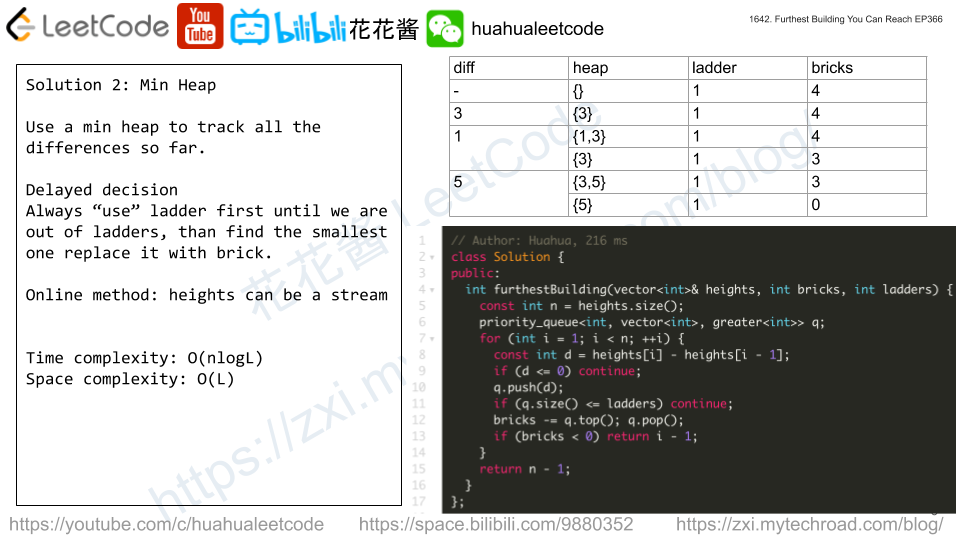
Use a min heap to store all the height differences ( > 0) so far, if heap size is greater than ladders, which means we have to use bricks, extract the smallest value and subtract the bricks.

Time complexity: O(nlogk)
Space complexity: O(n)

C++

// Author: Huahua, 216 ms

class Solution {

public:

int furthestBuilding(vector<int>& heights, int bricks, int ladders) {

const int n = heights.size();

priority_queue<int, vector<int>, greater<int>> q;

for (int i = 1; i < n; ++i) {

const int d = heights[i] - heights[i - 1];

if (d <= 0) continue;

q.push(d);

if (q.size() <= ladders) continue;

bricks -= q.top(); q.pop();

if (bricks < 0) return i - 1;

}

return n - 1;

}

};

花花酱 LeetCode 1641. Count Sorted Vowel Strings

By zxi on November 1, 2020

Given an integer n, return the number of strings of length n that consist only of vowels (a, e, i, o, u) and are lexicographically sorted.

A string s is lexicographically sorted if for all valid i, s[i] is the same as or comes before s[i+1] in the alphabet.

Example 1:

Input: n = 1
Output: 5
Explanation: The 5 sorted strings that consist of vowels only are ["a","e","i","o","u"].

Example 2:

Input: n = 2
Output: 15
Explanation: The 15 sorted strings that consist of vowels only are
["aa","ae","ai","ao","au","ee","ei","eo","eu","ii","io","iu","oo","ou","uu"].
Note that "ea" is not a valid string since 'e' comes after 'a' in the alphabet.

Example 3:

Input: n = 33
Output: 66045

Solution: DP

dp[i][j] := # of strings of length i ends with j.

dp[i][j] = sum(dp[i – 1][[k]) 0 <= k <= j

Time complexity: O(n)
Space complexity: O(n) -> O(1)

C++/O(n) Space

class Solution {

public:

int countVowelStrings(int n) {

// dp[i][j] = # of strings of length i ends with j

vector<vector<int>> dp(n + 1, vector<int>(5, 1));

for (int i = 2; i <= n; ++i) {

int s = 0;

for (int j = 0; j < 5; ++j) {

s += dp[i - 1][j];

dp[i][j] = s;

}

return accumulate(begin(dp[n]), end(dp[n]), 0);

}

};

C++/O(1) Space

class Solution {

public:

int countVowelStrings(int n) {

// dp([i])[j] = # of strings of length i ends with j

vector<int> dp(5, 1);

for (int i = 2; i <= n; ++i)

for (int j = 4; j >= 0; --j)

for (int k = 0; k < j; ++k)

dp[j] += dp[k];

return accumulate(begin(dp), end(dp), 0);

}

};

花花酱 LeetCode 1640. Check Array Formation Through Concatenation

By zxi on October 31, 2020

You are given an array of distinct integers arr and an array of integer arrays pieces, where the integers in pieces are distinct. Your goal is to form arr by concatenating the arrays in pieces in any order. However, you are not allowed to reorder the integers in each array pieces[i].

Return true if it is possible to form the array arr from pieces. Otherwise, return false.

Example 1:

Input: arr = [85], pieces = [[85]]
Output: true

Example 2:

Input: arr = [15,88], pieces = [[88],[15]]
Output: true
Explanation: Concatenate [15] then [88]

Example 3:

Input: arr = [49,18,16], pieces = [[16,18,49]]
Output: false
Explanation: Even though the numbers match, we cannot reorder pieces[0].

Example 4:

Input: arr = [91,4,64,78], pieces = [[78],[4,64],[91]]
Output: true
Explanation: Concatenate [91] then [4,64] then [78]

Example 5:

Input: arr = [1,3,5,7], pieces = [[2,4,6,8]]
Output: false

Constraints:

1 <= pieces.length <= arr.length <= 100
sum(pieces[i].length) == arr.length
1 <= pieces[i].length <= arr.length
1 <= arr[i], pieces[i][j] <= 100
The integers in arr are distinct.
The integers in pieces are distinct (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct).

Solution: Hashtable

Store the index of the first number of each piece, for each number a in arr, concat the entire piece array whose first element equals to a.

Time complexity: O(n)
Space complexity: O(n)

C++

class Solution {

public:

bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {

unordered_map<int, int> m;

for (int i = 0; i < pieces.size(); ++i)

m[pieces[i][0]] = i;

vector<int> ans;

for (int a : arr) {

if (!m.count(a)) continue;

ans.insert(end(ans), begin(pieces[m[a]]), end(pieces[m[a]]));

}

return ans == arr;

}

};

花花酱 LeetCode 1639. Number of Ways to Form a Target String Given a Dictionary

By zxi on October 31, 2020

You are given a list of strings of the same length words and a string target.

Your task is to form target using the given words under the following rules:

target should be formed from left to right.
To form the i^th character (0-indexed) of target, you can choose the k^th character of the j^th string in words if target[i] = words[j][k].
Once you use the k^th character of the j^th string of words, you can no longer use the x^th character of any string in words where x <= k. In other words, all characters to the left of or at index k become unusuable for every string.
Repeat the process until you form the string target.

Notice that you can use multiple characters from the same string in words provided the conditions above are met.

Return the number of ways to form target from words. Since the answer may be too large, return it modulo 10⁹ + 7.

Example 1:

Input: words = ["acca","bbbb","caca"], target = "aba"
Output: 6
Explanation: There are 6 ways to form target.
"aba" -> index 0 ("acca"), index 1 ("bbbb"), index 3 ("caca")
"aba" -> index 0 ("acca"), index 2 ("bbbb"), index 3 ("caca")
"aba" -> index 0 ("acca"), index 1 ("bbbb"), index 3 ("acca")
"aba" -> index 0 ("acca"), index 2 ("bbbb"), index 3 ("acca")
"aba" -> index 1 ("caca"), index 2 ("bbbb"), index 3 ("acca")
"aba" -> index 1 ("caca"), index 2 ("bbbb"), index 3 ("caca")

Example 2:

Input: words = ["abba","baab"], target = "bab"
Output: 4
Explanation: There are 4 ways to form target.
"bab" -> index 0 ("baab"), index 1 ("baab"), index 2 ("abba")
"bab" -> index 0 ("baab"), index 1 ("baab"), index 3 ("baab")
"bab" -> index 0 ("baab"), index 2 ("baab"), index 3 ("baab")
"bab" -> index 1 ("abba"), index 2 ("baab"), index 3 ("baab")

Example 3:

Input: words = ["abcd"], target = "abcd"
Output: 1

Example 4:

Input: words = ["abab","baba","abba","baab"], target = "abba"
Output: 16

Constraints:

1 <= words.length <= 1000
1 <= words[i].length <= 1000
All strings in words have the same length.
1 <= target.length <= 1000
words[i] and target contain only lowercase English letters.

Solution: DP

dp[i][j] := # of ways to form target[0~j] where the j-th letter is from the i-th column of words.
count[i][j] := # of words that have word[i] == target[j]

dp[i][j] = dp[i-1][j-1] * count[i][j]

Time complexity: O(mn)
Space complexity: O(mn) -> O(n)

C++

class Solution {

public:

int numWays(vector<string>& words, string target) {

constexpr int kMod = 1e9 + 7;

const int n = target.length();

const int m = words[0].length();

vector<long> dp(n); // dp[j] = # of ways to form t[0~j]

for (int i = 0; i < m; ++i) {

vector<int> count(26);

for (const string& word: words)

++count[word[i] - 'a'];

for (int j = min(i, n - 1); j >= 0; --j)

dp[j] = (dp[j] + (j > 0 ? dp[j - 1] : 1) *

count[target[j] - 'a']) % kMod;

}

return dp[n - 1];

}

};

花花酱 LeetCode 1638. Count Substrings That Differ by One Character

By zxi on October 31, 2020

Given two strings s and t, find the number of ways you can choose a non-empty substring of s and replace a single character by a different character such that the resulting substring is a substring of t. In other words, find the number of substrings in s that differ from some substring in t by exactly one character.

For example, the underlined substrings in "computer" and "computation" only differ by the 'e'/'a', so this is a valid way.

Return the number of substrings that satisfy the condition above.

A substring is a contiguous sequence of characters within a string.

Example 1:

Input: s = "aba", t = "baba"
Output: 6
Explanation: The following are the pairs of substrings from s and t that differ by exactly 1 character:
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
The underlined portions are the substrings that are chosen from s and t.

Example 2:

Input: s = "ab", t = "bb"
Output: 3
Explanation: The following are the pairs of substrings from s and t that differ by 1 character:
("ab", "bb")
("ab", "bb")
("ab", "bb")
The underlined portions are the substrings that are chosen from s and t.

Example 3:

Input: s = "a", t = "a"
Output: 0

Example 4:

Input: s = "abe", t = "bbc"
Output: 10

Constraints:

1 <= s.length, t.length <= 100
s and t consist of lowercase English letters only.

Solution1: All Pairs + Prefix Matching

match s[i:i+p] with t[j:j+p], is there is one missed char, increase the ans, until there are two miss matched chars or reach the end.

Time complexity: O(m*n*min(m,n))
Space complexity: O(1)

C++

class Solution {

public:

int countSubstrings(string s, string t) {

const int m = s.length();

const int n = t.length();

int ans = 0, diff = 0;

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j, diff = 0)

for (int p = 0; i + p < m && j + p < n && diff <= 1; ++p)

if ((diff += (s[i + p] != t[j + p])) == 1) ++ans;

return ans;

}

};

Solution 2: Continuous Matching

Start matching s[0] with t[j] and s[i] with t[0]

Time complexity: O(mn)
Space complexity: O(1)

C++

class Solution {

public:

int countSubstrings(string s, string t) {

const int m = s.length();

const int n = t.length();

int ans = 0;

auto helper = [&](int i, int j) {

for (int cur = 0, pre = 0; i < m && j < n; ++i, ++j) {

++cur;

if (s[i] != t[j]) {

pre = cur;

cur = 0;

}

ans += pre;

}

};

for (int i = 0; i < m; ++i) helper(i, 0);

for (int j = 1; j < n; ++j) helper(0, j);

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1642. Furthest Building You Can Reach

Solution 0: DFS

Solution 1: Binary Search + Greedy

C++

Solution 2: Min heap

C++

花花酱 LeetCode 1641. Count Sorted Vowel Strings

Solution: DP

C++/O(n) Space

C++/O(1) Space

花花酱 LeetCode 1640. Check Array Formation Through Concatenation

Solution: Hashtable

C++

花花酱 LeetCode 1639. Number of Ways to Form a Target String Given a Dictionary

Solution: DP

C++

花花酱 LeetCode 1638. Count Substrings That Differ by One Character

Solution1: All Pairs + Prefix Matching

C++

Solution 2: Continuous Matching

C++