Huahua’s Tech Road

花花酱 LeetCode 1599. Maximum Profit of Operating a Centennial Wheel

By zxi on September 27, 2020

You are the operator of a Centennial Wheel that has four gondolas, and each gondola has room for up to four people. You have the ability to rotate the gondolas counterclockwise, which costs you runningCost dollars.

You are given an array customers of length n where customers[i] is the number of new customers arriving just before the i^th rotation (0-indexed). This means you must rotate the wheel i times before customers[i] arrive. Each customer pays boardingCost dollars when they board on the gondola closest to the ground and will exit once that gondola reaches the ground again.

You can stop the wheel at any time, including before serving all customers. If you decide to stop serving customers, all subsequent rotations are free in order to get all the customers down safely. Note that if there are currently more than four customers waiting at the wheel, only four will board the gondola, and the rest will wait for the next rotation.

Return the minimum number of rotations you need to perform to maximize your profit. If there is no scenario where the profit is positive, return -1.

Example 1:

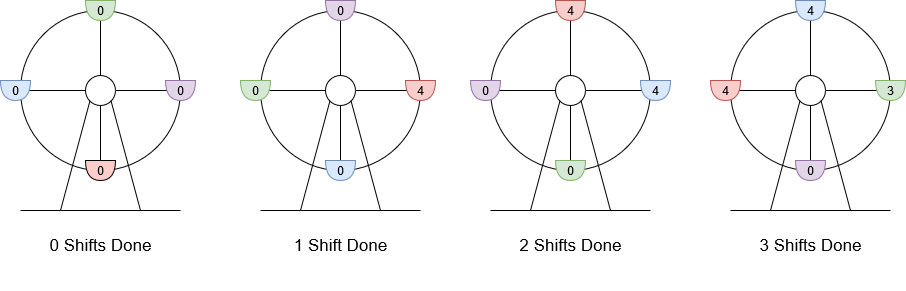
Input: customers = [8,3], boardingCost = 5, runningCost = 6
Output: 3
Explanation: The numbers written on the gondolas are the number of people currently there.
1. 8 customers arrive, 4 board and 4 wait for the next gondola, the wheel rotates. Current profit is 4 * $5 - 1 * $6 = $14.
2. 3 customers arrive, the 4 waiting board the wheel and the other 3 wait, the wheel rotates. Current profit is 8 * $5 - 2 * $6 = $28.
3. The final 3 customers board the gondola, the wheel rotates. Current profit is 11 * $5 - 3 * $6 = $37.
The highest profit was $37 after rotating the wheel 3 times.

Example 2:

Input: customers = [10,9,6], boardingCost = 6, runningCost = 4
Output: 7
Explanation:
1. 10 customers arrive, 4 board and 6 wait for the next gondola, the wheel rotates. Current profit is 4 * $6 - 1 * $4 = $20.
2. 9 customers arrive, 4 board and 11 wait (2 originally waiting, 9 newly waiting), the wheel rotates. Current profit is 8 * $6 - 2 * $4 = $40.
3. The final 6 customers arrive, 4 board and 13 wait, the wheel rotates. Current profit is 12 * $6 - 3 * $4 = $60.
4. 4 board and 9 wait, the wheel rotates. Current profit is 16 * $6 - 4 * $4 = $80.
5. 4 board and 5 wait, the wheel rotates. Current profit is 20 * $6 - 5 * $4 = $100.
6. 4 board and 1 waits, the wheel rotates. Current profit is 24 * $6 - 6 * $4 = $120.
7. 1 boards, the wheel rotates. Current profit is 25 * $6 - 7 * $4 = $122.
The highest profit was $122 after rotating the wheel 7 times.

Example 3:

Input: customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
Output: -1
Explanation:
1. 3 customers arrive, 3 board and 0 wait, the wheel rotates. Current profit is 3 * $1 - 1 * $92 = -$89.
2. 4 customers arrive, 4 board and 0 wait, the wheel rotates. Current profit is 7 * $1 - 2 * $92 = -$177.
3. 0 customers arrive, 0 board and 0 wait, the wheel rotates. Current profit is 7 * $1 - 3 * $92 = -$269.
4. 5 customers arrive, 4 board and 1 waits, the wheel rotates. Current profit is 12 * $1 - 4 * $92 = -$356.
5. 1 customer arrives, 2 board and 0 wait, the wheel rotates. Current profit is 13 * $1 - 5 * $92 = -$447.
The profit was never positive, so return -1.

Example 4:

Input: customers = [10,10,6,4,7], boardingCost = 3, runningCost = 8
Output: 9
Explanation:
1. 10 customers arrive, 4 board and 6 wait, the wheel rotates. Current profit is 4 * $3 - 1 * $8 = $4.
2. 10 customers arrive, 4 board and 12 wait, the wheel rotates. Current profit is 8 * $3 - 2 * $8 = $8.
3. 6 customers arrive, 4 board and 14 wait, the wheel rotates. Current profit is 12 * $3 - 3 * $8 = $12.
4. 4 customers arrive, 4 board and 14 wait, the wheel rotates. Current profit is 16 * $3 - 4 * $8 = $16.
5. 7 customers arrive, 4 board and 17 wait, the wheel rotates. Current profit is 20 * $3 - 5 * $8 = $20.
6. 4 board and 13 wait, the wheel rotates. Current profit is 24 * $3 - 6 * $8 = $24.
7. 4 board and 9 wait, the wheel rotates. Current profit is 28 * $3 - 7 * $8 = $28.
8. 4 board and 5 wait, the wheel rotates. Current profit is 32 * $3 - 8 * $8 = $32.
9. 4 board and 1 waits, the wheel rotates. Current profit is 36 * $3 - 9 * $8 = $36.
10. 1 board and 0 wait, the wheel rotates. Current profit is 37 * $3 - 10 * $8 = $31.
The highest profit was $36 after rotating the wheel 9 times.

Constraints:

n == customers.length
1 <= n <= 10⁵
0 <= customers[i] <= 50
1 <= boardingCost, runningCost <= 100

Solution: Simulation

Process if waiting customers > 0 or i < n.

Pruning, if runningCost > 4 * boardingCost (max revenue), there is no way to make profit.

Time complexity: sum(consumers) / 4
Space complexity: O(1)

C++

class Solution {

public:

int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {

const int n = customers.size();

constexpr int kMaxC = 4;

if (runningCost > kMaxC * boardingCost) return -1;

int c = 0;

int ans = -1;

int p = 0;

int max_p = 0;

for (int r = 0; r < n || c > 0; ++r) {

c += (r < n ? customers[r] : 0);

p += min(c, kMaxC) * boardingCost - runningCost;

c -= min(c, kMaxC);

if (p > max_p) {

max_p = p;

ans = r + 1; // 1-based

}

return ans;

}

};

花花酱 LeetCode 1598. Crawler Log Folder

By zxi on September 27, 2020

The Leetcode file system keeps a log each time some user performs a change folder operation.

The operations are described below:

"../" : Move to the parent folder of the current folder. (If you are already in the main folder, remain in the same folder).
"./" : Remain in the same folder.
"x/" : Move to the child folder named x (This folder is guaranteed to always exist).

You are given a list of strings logs where logs[i] is the operation performed by the user at the i^th step.

The file system starts in the main folder, then the operations in logs are performed.

Return the minimum number of operations needed to go back to the main folder after the change folder operations.

Example 1:

Input: logs = ["d1/","d2/","../","d21/","./"]
Output: 2
Explanation: Use this change folder operation "../" 2 times and go back to the main folder.

Example 2:

Input: logs = ["d1/","d2/","./","d3/","../","d31/"]
Output: 3

Example 3:

Input: logs = ["d1/","../","../","../"]
Output: 0

Constraints:

1 <= logs.length <= 10³
2 <= logs[i].length <= 10
logs[i] contains lowercase English letters, digits, '.', and '/'.
logs[i] follows the format described in the statement.
Folder names consist of lowercase English letters and digits.

Solution: Simulation

We only need to track the depth of current folder, and name and path can be ignored.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minOperations(vector<string>& logs) {

int ans = 0;

for (const string& log : logs) {

if (log == "../")

ans = max(ans - 1, 0);

else if (log != "./")

++ans;

}

return ans;

}

};

花花酱 LeetCode 1595. Minimum Cost to Connect Two Groups of Points

By zxi on September 23, 2020

You are given two groups of points where the first group has size₁ points, the second group has size₂ points, and size₁ >= size₂.

The cost of the connection between any two points are given in an size₁ x size₂ matrix where cost[i][j] is the cost of connecting point i of the first group and point j of the second group. The groups are connected if each point in both groups is connected to one or more points in the opposite group. In other words, each point in the first group must be connected to at least one point in the second group, and each point in the second group must be connected to at least one point in the first group.

Return the minimum cost it takes to connect the two groups.

Example 1:

Input: cost = [[15, 96], [36, 2]]
Output: 17
Explanation: The optimal way of connecting the groups is:
1--A
2--B
This results in a total cost of 17.

Example 2:

Input: cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
Output: 4
Explanation: The optimal way of connecting the groups is:
1--A
2--B
2--C
3--A
This results in a total cost of 4.
Note that there are multiple points connected to point 2 in the first group and point A in the second group. This does not matter as there is no limit to the number of points that can be connected. We only care about the minimum total cost.

Example 3:

Input: cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
Output: 10

Constraints:

size₁ == cost.length
size₂ == cost[i].length
1 <= size₁, size₂ <= 12
size₁ >= size₂
0 <= cost[i][j] <= 100

Solution 1: Bistmask DP

dp[i][s] := min cost to connect first i (1-based) points in group1 and a set of points (represented by a bitmask s) in group2.

ans = dp[m][1 << n – 1]

dp[i][s | (1 << j)] := min(dp[i][s] + cost[i][j], dp[i-1][s] + cost[i][j])

Time complexity: O(m*n*2^n)
Space complexity: O(m*2^n)

C++/Bottom up

class Solution {

public:

int connectTwoGroups(vector<vector<int>>& cost) {

constexpr int kInf = 1e9;

const int m = cost.size();

const int n = cost[0].size();

// dp[i][s] := min cost to connect first i points in group1

// and points (bitmask s) in group2.

vector<vector<int>> dp(m + 1, vector<int>(1 << n, kInf));

dp[0][0] = 0;

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

for (int s = 0; s < 1 << n; ++s)

dp[i + 1][s | (1 << j)] = min({dp[i + 1][s | (1 << j)],

dp[i + 1][s] + cost[i][j],

dp[i][s] + cost[i][j]});

return dp[m].back();

}

};

花花酱 LeetCode 1594. Maximum Non Negative Product in a Matrix

By zxi on September 21, 2020

You are given a rows x cols matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.

Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (rows - 1, cols - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.

Return the maximum non-negative product modulo 10⁹ + 7. If the maximum product is negative return -1.

Notice that the modulo is performed after getting the maximum product.

Example 1:

Input: grid = [[-1,-2,-3],
               [-2,-3,-3],
               [-3,-3,-2]]
Output: -1
Explanation: It's not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.

Example 2:

Input: grid = [[1,-2,1],
               [1,-2,1],
               [3,-4,1]]
Output: 8
Explanation: Maximum non-negative product is in bold (1 * 1 * -2 * -4 * 1 = 8).

Example 3:

Input: grid = [[1, 3],
               [0,-4]]
Output: 0
Explanation: Maximum non-negative product is in bold (1 * 0 * -4 = 0).

Example 4:

Input: grid = [[ 1, 4,4,0],
               [-2, 0,0,1],
               [ 1,-1,1,1]]
Output: 2
Explanation: Maximum non-negative product is in bold (1 * -2 * 1 * -1 * 1 * 1 = 2).

Constraints:

1 <= rows, cols <= 15
-4 <= grid[i][j] <= 4

Solution: DP

Use two dp arrays,

dp_max[i][j] := max product of matrix[0~i][0~j]
dp_min[i][j] := min product of matrix[0~i][0~j]

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

// Author: Huahua

class Solution {

public:

int maxProductPath(vector<vector<int>>& grid) {

constexpr int kMod = 1e9 + 7;

const int m = grid.size();

const int n = grid[0].size();

vector<vector<long>> dp_max(m, vector<long>(n));

vector<vector<long>> dp_min(m, vector<long>(n));

dp_max[0][0] = dp_min[0][0] = grid[0][0];

for (int i = 1; i < m; ++i)

dp_max[i][0] = dp_min[i][0] = dp_min[i - 1][0] * grid[i][0];

for (int j = 1; j < n; ++j)

dp_max[0][j] = dp_min[0][j] = dp_min[0][j - 1] * grid[0][j];

for (int i = 1; i < m; ++i)

for (int j = 1; j < n; ++j) {

if (grid[i][j] >= 0) {

dp_max[i][j] = max(dp_max[i - 1][j], dp_max[i][j - 1]) * grid[i][j];

dp_min[i][j] = min(dp_min[i - 1][j], dp_min[i][j - 1]) * grid[i][j];

} else {

dp_max[i][j] = min(dp_min[i - 1][j], dp_min[i][j - 1]) * grid[i][j];

dp_min[i][j] = max(dp_max[i - 1][j], dp_max[i][j - 1]) * grid[i][j];

}

return dp_max[m - 1][n - 1] >= 0 ? dp_max[m - 1][n - 1] % kMod : -1;

}

};

花花酱 LeetCode 1593. Split a String Into the Max Number of Unique Substrings

By zxi on September 21, 2020

Given a string s, return the maximum number of unique substrings that the given string can be split into.

You can split string s into any list of non-empty substrings, where the concatenation of the substrings forms the original string. However, you must split the substrings such that all of them are unique.

A substring is a contiguous sequence of characters within a string.

Example 1:

Input: s = "ababccc"
Output: 5
Explanation: One way to split maximally is ['a', 'b', 'ab', 'c', 'cc']. Splitting like ['a', 'b', 'a', 'b', 'c', 'cc'] is not valid as you have 'a' and 'b' multiple times.

Example 2:

Input: s = "aba"
Output: 2
Explanation: One way to split maximally is ['a', 'ba'].

Example 3:

Input: s = "aa"
Output: 1
Explanation: It is impossible to split the string any further.

Constraints:

1 <= s.length <= 16
s contains only lower case English letters.

Solution: Brute Force

Try all combinations.
Time complexity: O(2^n)
Space complexity: O(n)

Iterative/C++

// Author: Huahua

class Solution {

public:

int maxUniqueSplit(string_view s) {

const int n = s.length();

if (n == 1) return 1;

size_t ans = 1;

unordered_set<string_view> seen;

for (int m = 1; m < 1 << (n - 1); ++m) {

if (__builtin_popcount(m) < ans) continue; // 956 ms -> 52 ms

bool valid = true;

int p = 0;

for (int i = 1; i <= n && valid; ++i) {

if (m & (1 << (i - 1)) || i == n) {

valid &= seen.insert(s.substr(p, i - p)).second;

p = i;

}

if (valid) ans = max(ans, seen.size());

seen.clear();

}

return ans;

}

};

DFS/C++

// Author: Huahua

class Solution {

public:

int maxUniqueSplit(string_view s) {

size_t ans = 1;

const int n = s.length();

unordered_set<string_view> seen;

function<void(int)> dfs = [&](int p) {

if (p == n) {

ans = max(ans, seen.size());

return;

}

for (int i = p; i < n; ++i) {

string_view ss = s.substr(p, i - p + 1);

if (!seen.insert(ss).second) continue;

dfs(i + 1);

seen.erase(ss);

}

};

dfs(0);

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1599. Maximum Profit of Operating a Centennial Wheel

Solution: Simulation

C++

花花酱 LeetCode 1598. Crawler Log Folder

Solution: Simulation

C++

花花酱 LeetCode 1595. Minimum Cost to Connect Two Groups of Points

Solution 1: Bistmask DP

C++/Bottom up

花花酱 LeetCode 1594. Maximum Non Negative Product in a Matrix

Solution: DP

C++

花花酱 LeetCode 1593. Split a String Into the Max Number of Unique Substrings

Solution: Brute Force

Iterative/C++

DFS/C++