Huahua’s Tech Road

花花酱 LeetCode 1235. Maximum Profit in Job Scheduling

By zxi on October 24, 2019

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You’re given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

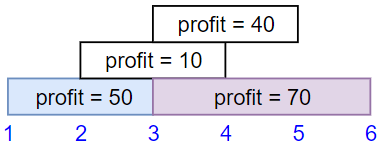
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:


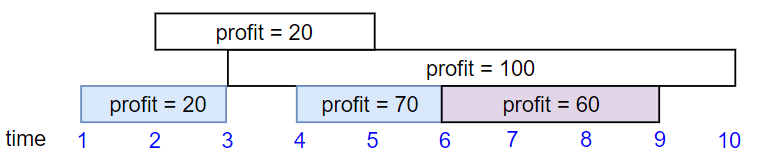
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4

Solution: DP + binary search

Sort jobs by ending time.
dp[t] := max profit by end time t.

for a job = (s, e, p)
dp[e] = dp[u] + p, u <= s, and if dp[u] + p > last_element in dp.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {

const int n = startTime.size();

vector<vector<int>> jobs(n);

for (int i = 0; i < n; ++i)

jobs[i] = {endTime[i], startTime[i], profit[i]};

sort(begin(jobs), end(jobs));

int ans = 0;

map<int, int> m{{0, 0}}; // {end_time -> max_profit}

for (const auto& job : jobs) {

int p = prev(m.upper_bound(job[1]))->second + job[2];

if (p > rbegin(m)->second) {

m[job[0]] = p;

}

return rbegin(m)->second;

}

};

花花酱 LeetCode 1233. Remove Sub-Folders from the Filesystem

By zxi on October 21, 2019

Given a list of folders, remove all sub-folders in those folders and return in any order the folders after removing.

If a folder[i] is located within another folder[j], it is called a sub-folder of it.

The format of a path is one or more concatenated strings of the form: / followed by one or more lowercase English letters. For example, /leetcode and /leetcode/problems are valid paths while an empty string and / are not.

Example 1:

Input: folder = ["/a","/a/b","/c/d","/c/d/e","/c/f"]
Output: ["/a","/c/d","/c/f"]
Explanation: Folders "/a/b/" is a subfolder of "/a" and "/c/d/e" is inside of folder "/c/d" in our filesystem.

Example 2:

Input: folder = ["/a","/a/b/c","/a/b/d"]
Output: ["/a"]
Explanation: Folders "/a/b/c" and "/a/b/d/" will be removed because they are subfolders of "/a".

Example 3:

Input: folder = ["/a/b/c","/a/b/ca","/a/b/d"]
Output: ["/a/b/c","/a/b/ca","/a/b/d"]

Constraints:

1 <= folder.length <= 4 * 10^4
2 <= folder[i].length <= 100
folder[i] contains only lowercase letters and ‘/’
folder[i] always starts with character ‘/’
Each folder name is unique.

Solution: HashTable

Time complexity: O(n*L)
Space complexity: O(n*L)

C++

// Author: Huahua

class Solution {

public:

vector<string> removeSubfolders(vector<string>& folder) {

unordered_set<string> s(begin(folder), end(folder));

vector<string> ans;

for (const auto& cur : folder) {

string f = cur;

bool valid = true;

while (!f.empty() && valid) {

while (f.back() != '/') f.pop_back();

f.pop_back();

if (s.count(f)) valid = false;

}

if (valid) ans.push_back(cur);

}

return ans;

}

};

花花酱 LeetCode 1230. Toss Strange Coins

By zxi on October 19, 2019

You have some coins. The i-th coin has a probability prob[i] of facing heads when tossed.

Return the probability that the number of coins facing heads equals target if you toss every coin exactly once.

Example 1:

Input: prob = [0.4], target = 1
Output: 0.40000

Example 2:

Input: prob = [0.5,0.5,0.5,0.5,0.5], target = 0
Output: 0.03125

Constraints:

1 <= prob.length <= 1000
0 <= prob[i] <= 1
0 <= target <= prob.length
Answers will be accepted as correct if they are within 10^-5 of the correct answer.

Solution: DP

dp[i][j] := prob of j coins face up after tossing first i coins.
dp[i][j] = dp[i-1][j] * (1 – p[i]) + dp[i-1][j-1] * p[i]

Time complexity: O(n^2)
Space complexity: O(n^2) -> O(n)

C++

// Author: Huahua

class Solution {

public:

double probabilityOfHeads(vector<double>& prob, int target) {

const int n = prob.size();

vector<double> dp(target + 1);

dp[0] = 1.0;

for (int i = 0; i < n; ++i)

for (int j = min(i + 1, target); j >= 0; --j)

dp[j] = dp[j] * (1 - prob[i]) + (j > 0 ? dp[j - 1] : 0) * prob[i];

return dp[target];

}

};

Solution 2: Recursion + Memorization

Time complexity: O(n^2)
Space complexity: O(n^2)

C++

// Author: Huahua

class Solution {

public:

double probabilityOfHeads(vector<double>& prob, int target) {

vector<vector<double>> mem(prob.size() + 1, vector<double>(target + 1, -1));

function<double(int, int)> dp = [&](int n, int k) {

if (k > n || k < 0) return 0.0;

if (n == 0) return 1.0;

if (mem[n][k] >= 0) return mem[n][k];

const double p = prob[n - 1];

return mem[n][k] = p * dp(n - 1, k - 1) + (1 - p) * dp(n - 1, k);

};

return dp(prob.size(), target);

}

};

花花酱 LeetCode 1223. Dice Roll Simulation

By zxi on October 17, 2019

A die simulator generates a random number from 1 to 6 for each roll. You introduced a constraint to the generator such that it cannot roll the number i more than rollMax[i] (1-indexed) consecutive times.

Given an array of integers rollMax and an integer n, return the number of distinct sequences that can be obtained with exact n rolls.

Two sequences are considered different if at least one element differs from each other. Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: n = 2, rollMax = [1,1,2,2,2,3]
Output: 34
Explanation: There will be 2 rolls of die, if there are no constraints on the die, there are 6 * 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.

Example 2:

Input: n = 2, rollMax = [1,1,1,1,1,1]
Output: 30

Example 3:

Input: n = 3, rollMax = [1,1,1,2,2,3]
Output: 181

Constraints:

1 <= n <= 5000
rollMax.length == 6
1 <= rollMax[i] <= 15

Solutions: DP

Naive one:

def: dp[i][j][k] := # of sequences ends with k consecutive j after i rolls
Init: dp[1][*][1] = 1

transition:
dp[i][j][1] = sum(dp[i-1][p][*]), p != j
dp[i][j][k + 1] = dp[i-1][j]][k]

Time complexity: O(n*6*6*15)
Space complexity: O(n*6*15) -> O(6*15)

C++

// Author: Huahua

class Solution {

public:

int dieSimulator(int n, vector<int>& rollMax) {

constexpr int kMaxRolls = 15;

constexpr int kMod = 1e9 + 7;

// dp[i][j][k] := # of sequences ends with k consecutive j after i rolls

vector<vector<vector<int>>> dp(n + 1,

vector<vector<int>>(6, vector<int>(kMaxRolls + 1)));

for (int j = 0; j < 6; ++j)

dp[1][j][1] = 1; // 1 step, 1 dice, 1 way

for (int i = 2; i <= n; ++i)

for (int j = 0; j < 6; ++j)

for (int p = 0; p < 6; ++p)

for (int k = 1; k <= rollMax[p]; ++k)

if (p != j) // not the same dice

dp[i][j][1] = (dp[i][j][1] + dp[i - 1][p][k]) % kMod;

else if (k < rollMax[p]) // same dice, make sure k + 1 <= rollMax

dp[i][j][k + 1] = (dp[i][j][k + 1] + dp[i - 1][p][k]) % kMod;

int ans = 0;

for (int j = 0; j < 6; ++j)

for (int k = 1; k <= rollMax[j]; ++k)

ans = (ans + dp[n][j][k]) % kMod;

return ans;

}

};

Solution 2: DP with compressed state

dp[i][j] := # of sequences of length i end with j
dp[i][j] := sum(dp[i-1]) – invalid

Time complexity: O(n*6)
Space complexity: O(n*6)

C++

// Author: Huahua

class Solution {

public:

int dieSimulator(int n, vector<int>& rollMax) {

constexpr int kMod = 1e9 + 7;

// dp[i][j] := # of sequences ends with j after i rolls

vector<vector<int>> dp(n + 1, vector<int>(7));

vector<int> sums(n + 1); // sums[i] := sum(dp[i])

for (int j = 0; j < 6; ++j)

sums[1] += dp[1][j] = 1; // 1 roll, 1 dice, 1 way

for (int i = 2; i <= n; ++i)

for (int j = 0; j < 6; ++j) {

const int k = i - rollMax[j];

const int invalid = k <= 1 ? max(k, 0) : sums[k - 1] - dp[k - 1][j];

dp[i][j] = ((sums[i - 1] - invalid) % kMod + kMod) % kMod;

sums[i] = (sums[i] + dp[i][j]) % kMod;

}

return sums[n];

}

};

花花酱 LeetCode 1222. Queens That Can Attack the King

By zxi on October 14, 2019

On an 8×8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

Example 1:

Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:  
The queen at [0,1] can attack the king cause they're in the same row. 
The queen at [1,0] can attack the king cause they're in the same column. 
The queen at [3,3] can attack the king cause they're in the same diagnal. 
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:

Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

Example 3:

Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Constraints:

1 <= queens.length <= 63
queens[0].length == 2
0 <= queens[i][j] < 8
king.length == 2
0 <= king[0], king[1] < 8
At most one piece is allowed in a cell.

Solution2: Simulation

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {

vector<vector<int>> b(8, vector<int>(8));

for (const auto& q : queens)

b[q[0]][q[1]] = 1;

vector<vector<int>> ans;

for (const auto& q : queens) {

for (int dx = -1; dx <= 1; ++dx)

for (int dy = -1; dy <= 1; ++dy) {

if (dx == 0 && dy == 0) continue;

int x = q[1] + dx;

int y = q[0] + dy;

while (x >= 0 && y >= 0 && x < 8 && y < 8 && !b[y][x]) {

if (x == king[1] && y == king[0])

ans.push_back(q);

x += dx;

y += dy;

}

return ans;

}

};

Solution 2: HashTable + Binary Search

Time complexity: O(nlogn)
Space complexity: O(n)

Support arbitrarily large boards, e.g. 1e9 x 1e9 with 1e6 # of queens.

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {

unordered_map<int, map<int, vector<int>>> rows, cols, diag1, diag2;

for (const auto& q : queens) {

const int x = q[1];

const int y = q[0];

rows[y][x] = q;

cols[x][y] = q;

diag1[x + y][x] = q;

diag2[x - y][x] = q;

}

const int x = king[1];

const int y = king[0];

vector<vector<int>> ans;

find(rows, y, x, ans);

find(cols, x, y, ans);

find(diag1, x + y, x, ans);

find(diag2, x - y, x, ans);

return ans;

}

private:

void find(const unordered_map<int, map<int, vector<int>>>& m, int idx, int key, vector<vector<int>>& ans) {

if (!m.count(idx)) return;

const auto& d = m.at(idx);

auto it = d.upper_bound(key);

if (it != end(d))

ans.push_back(it->second);

if (it != begin(d))

ans.push_back(prev(it)->second);

}

};

Huahua's Tech Road

花花酱 LeetCode 1235. Maximum Profit in Job Scheduling

Solution: DP + binary search

C++

花花酱 LeetCode 1233. Remove Sub-Folders from the Filesystem

Solution: HashTable

C++

花花酱 LeetCode 1230. Toss Strange Coins

Solution: DP

C++

C++

花花酱 LeetCode 1223. Dice Roll Simulation

Solutions: DP

C++

Solution 2: DP with compressed state

C++

花花酱 LeetCode 1222. Queens That Can Attack the King

Solution2: Simulation

C++

Solution 2: HashTable + Binary Search

C++