Huahua’s Tech Road

花花酱 LeetCode 1267. Count Servers that Communicate

By zxi on November 23, 2019

You are given a map of a server center, represented as a m * n integer matrix grid, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.

Return the number of servers that communicate with any other server.

Example 1:

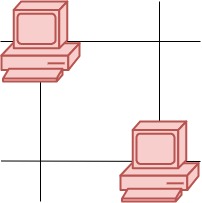
Input: grid = [[1,0],[0,1]]
Output: 0
Explanation: No servers can communicate with others.

Example 2:

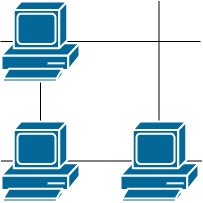
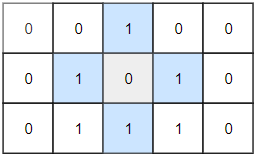
Input: grid = [[1,0],[1,1]]
Output: 3
Explanation: All three servers can communicate with at least one other server.

Example 3:

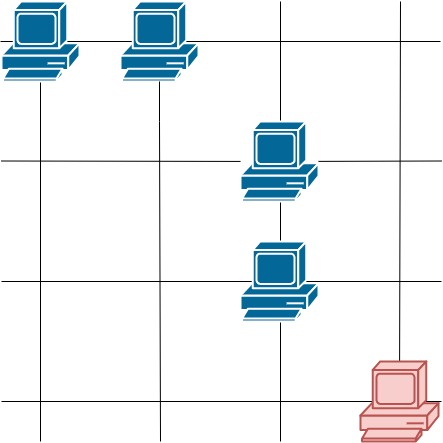
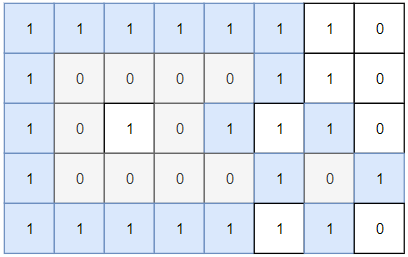
Input: grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]]
Output: 4
Explanation: The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.

Constraints:

m == grid.length
n == grid[i].length
1 <= m <= 250
1 <= n <= 250
grid[i][j] == 0 or 1

Solution: Counting

Two passes:
First pass, count number of computers for each row and each column.
Second pass, count grid[i][j] if rows[i] or cols[j] has more than 1 computer.

Time complexity: O(m*n)
Space complexity: O(m + n)

C++

// Author: Huahua

class Solution {

public:

int countServers(vector<vector<int>>& grid) {

const size_t m = grid.size();

const size_t n = grid[0].size();

vector<int> rows(m);

vector<int> cols(n);

for (size_t i = 0; i < m; ++i)

for (size_t j = 0; j < n; ++j) {

rows[i] += grid[i][j];

cols[j] += grid[i][j];

}

int ans = 0;

for (size_t i = 0; i < m; ++i)

for (size_t j = 0; j < n; ++j)

ans += (rows[i] > 1 || cols[j] > 1) ? grid[i][j] : 0;

return ans;

}

};

花花酱 LeetCode 1266. Minimum Time Visiting All Points

By zxi on November 23, 2019

On a plane there are n points with integer coordinates points[i] = [xi, yi]. Your task is to find the minimum time in seconds to visit all points.

You can move according to the next rules:

In one second always you can either move vertically, horizontally by one unit or diagonally (it means to move one unit vertically and one unit horizontally in one second).
You have to visit the points in the same order as they appear in the array.

Example 1:

Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2:

Input: points = [[3,2],[-2,2]]
Output: 5

Constraints:

points.length == n
1 <= n <= 100
points[i].length == 2
-1000 <= points[i][0], points[i][1] <= 1000

Solution: Geometry + Greedy

dx = abs(x1 – x2)
dy = abs(y1 – y2)

go diagonally first for min(dx, dy) steps, and then go straight line for abs(dx – dy) steps.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minTimeToVisitAllPoints(vector<vector<int>>& points) {

int ans = 0;

for (size_t i = 1; i < points.size(); ++i) {

int dx = abs(points[i - 1][0] - points[i][0]);

int dy = abs(points[i - 1][1] - points[i][1]);

ans += min(dx, dy) + abs(dx - dy);

}

return ans;

}

};

花花酱 LeetCode 1255. Maximum Score Words Formed by Letters

By zxi on November 9, 2019

Given a list of words, list of single letters (might be repeating) and score of every character.

Return the maximum score of any valid set of words formed by using the given letters (words[i] cannot be used two or more times).

It is not necessary to use all characters in letters and each letter can only be used once. Score of letters 'a', 'b', 'c', … ,'z' is given by score[0], score[1], … , score[25] respectively.

Example 1:

Input: words = ["dog","cat","dad","good"], letters = ["a","a","c","d","d","d","g","o","o"], score = [1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0]
Output: 23
Explanation:
Score  a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad" (5+1+5) and "good" (3+2+2+5) with a score of 23.
Words "dad" and "dog" only get a score of 21.

Example 2:

Input: words = ["xxxz","ax","bx","cx"], letters = ["z","a","b","c","x","x","x"], score = [4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10]
Output: 27
Explanation:
Score  a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax" (4+5), "bx" (4+5) and "cx" (4+5) with a score of 27.
Word "xxxz" only get a score of 25.

Example 3:

Input: words = ["leetcode"], letters = ["l","e","t","c","o","d"], score = [0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0]
Output: 0
Explanation:
Letter "e" can only be used once.

Constraints:

1 <= words.length <= 14
1 <= words[i].length <= 15
1 <= letters.length <= 100
letters[i].length == 1
score.length == 26
0 <= score[i] <= 10
words[i], letters[i] contains only lower case English letters.

Solution: Combination

Time complexity: O(2^n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maxScoreWords(vector<string>& words, vector<char>& letters, vector<int>& score) {

vector<int> counts(26);

vector<int> scores(words.size());

for (char c : letters) ++counts[c - 'a'];

for (int i = 0; i < words.size(); ++i)

for (char c : words[i]) scores[i] += score[c - 'a'];

int ans = 0;

function<void(int, int)> dfs = [&](int s, int cur) {

if (cur > ans) ans = cur;

for (int i = s; i < words.size(); ++i) {

bool valid = true;

for (char c : words[i]) valid &= --counts[c - 'a'] >= 0;

if (valid) dfs(i + 1, cur + scores[i]);

for (char c : words[i]) ++counts[c - 'a'];

}

};

dfs(0, 0);

return ans;

}

};

花花酱 LeetCode 1253. Reconstruct a 2-Row Binary Matrix

By zxi on November 9, 2019

Given the following details of a matrix with n columns and 2 rows :

The matrix is a binary matrix, which means each element in the matrix can be 0 or 1.
The sum of elements of the 0-th(upper) row is given as upper.
The sum of elements of the 1-st(lower) row is given as lower.
The sum of elements in the i-th column(0-indexed) is colsum[i], where colsum is given as an integer array with length n.

Your task is to reconstruct the matrix with upper, lower and colsum.

Return it as a 2-D integer array.

If there are more than one valid solution, any of them will be accepted.

If no valid solution exists, return an empty 2-D array.

Example 1:

Input: upper = 2, lower = 1, colsum = [1,1,1]
Output: [[1,1,0],[0,0,1]]
Explanation: [[1,0,1],[0,1,0]], and [[0,1,1],[1,0,0]] are also correct answers.

Example 2:

Input: upper = 2, lower = 3, colsum = [2,2,1,1]
Output: []

Example 3:

Input: upper = 5, lower = 5, colsum = [2,1,2,0,1,0,1,2,0,1]
Output: [[1,1,1,0,1,0,0,1,0,0],[1,0,1,0,0,0,1,1,0,1]]

Constraints:

1 <= colsum.length <= 10^5
0 <= upper, lower <= colsum.length
0 <= colsum[i] <= 2

Solution: Greedy?

Two passes:
first pass, only process sum = 2, upper = 1, lower = 1
second pass, only process sum = 1, whoever has more leftover, assign 1 to that row.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {

const int n = colsum.size();

vector<vector<int>> a(2, vector<int>(n));

for (int i = 0; i < n; ++i)

if (colsum[i] == 2) {

a[0][i] = a[1][i] = 1;

--upper;

--lower;

}

for (int i = 0; i < n; ++i)

if (colsum[i] == 1)

if (upper > lower) {

a[0][i] = 1;

--upper;

} else {

a[1][i] = 1;

--lower;

}

if (upper != 0 || lower != 0) return {};

return a;

}

};

花花酱 LeetCode 1254. Number of Closed Islands

By zxi on November 9, 2019

Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example 1:

Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

Constraints:

1 <= grid.length, grid[0].length <= 100
0 <= grid[i][j] <=1

Solution: DFS/Backtracking

For each connected component, if it can reach the boundary then it’s not a closed island.

Time complexity: O(n*m)
Space complexity: O(n*m)

C++

// Author: Huahua

class Solution {

public:

int closedIsland(vector<vector<int>>& grid) {

const int n = grid.size();

const int m = grid[0].size();

function<int(int, int)> dfs = [&](int x, int y) {

if (x < 0 || y < 0 || x >= m || y >= n) return 0;

if (grid[y][x]++) return 1;

return dfs(x + 1, y) & dfs(x - 1, y) & dfs(x, y + 1) & dfs(x, y - 1);

};

int ans = 0;

for (int i = 0; i < n; ++i)

for (int j = 0; j < m; ++j)

if (!grid[i][j]) ans += dfs(j, i);

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1267. Count Servers that Communicate

Solution: Counting

C++

花花酱 LeetCode 1266. Minimum Time Visiting All Points

C++

花花酱 LeetCode 1255. Maximum Score Words Formed by Letters

Solution: Combination

C++

花花酱 LeetCode 1253. Reconstruct a 2-Row Binary Matrix

Solution: Greedy?

C++

花花酱 LeetCode 1254. Number of Closed Islands

Solution: DFS/Backtracking

C++