花花酱 LeetCode 841. Keys and Rooms

By zxi on May 27, 2018

Problem

There are N rooms and you start in room 0. Each room has a distinct number in 0, 1, 2, ..., N-1, and each room may have some keys to access the next room.

Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, ..., N-1] where N = rooms.length. A key rooms[i][j] = v opens the room with number v.

Initially, all the rooms start locked (except for room 0).

You can walk back and forth between rooms freely.

Return true if and only if you can enter every room.

Example 1:

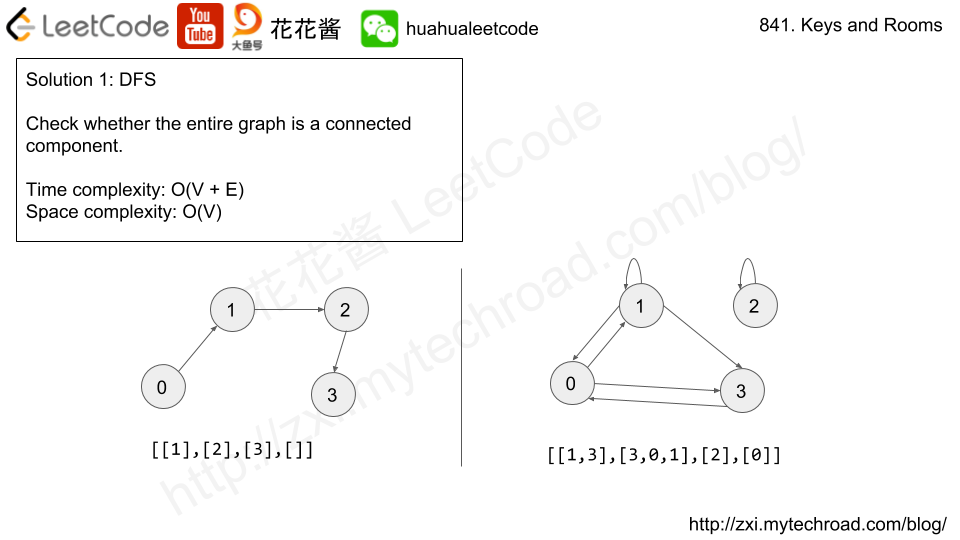
Input: [[1],[2],[3],[]]
Output: true
Explanation:  
We start in room 0, and pick up key 1.
We then go to room 1, and pick up key 2.
We then go to room 2, and pick up key 3.
We then go to room 3.  Since we were able to go to every room, we return true.

Example 2:

Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can't enter the room with number 2.

Note:

1 <= rooms.length <= 1000
0 <= rooms[i].length <= 1000
The number of keys in all rooms combined is at most 3000.

Solution: DFS

Time complexity: O(V + E)

Space complexity: O(V)

C++

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

bool canVisitAllRooms(vector<vector<int>>& rooms) {

unordered_set<int> visited;

dfs(rooms, 0, visited);

return visited.size() == rooms.size();

}

private:

void dfs(const vector<vector<int>>& rooms,

int cur, unordered_set<int>& visited) {

if (visited.count(cur)) return;

visited.insert(cur);

for (int nxt : rooms[cur])

dfs(rooms, nxt, visited);

}

};

花花酱 LeetCode 329. Longest Increasing Path in a Matrix

By zxi on May 24, 2018

Problem

Given an integer matrix, find the length of the longest increasing path.

From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).

Example 1:

Input: nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
Output: 4 
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

Input: nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
] 
Output: 4 
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Solution1: DFS + Memorization

Time complexity: O(mn)

Space complexity: O(mn)

C++

// Author: Huahua

// Running time: 36 ms

class Solution {

public:

int longestIncreasingPath(vector<vector<int>>& matrix) {

if (matrix.empty()) return 0;

m_ = matrix.size();

n_ = matrix[0].size();

dp_ = vector<vector<int>>(m_, vector<int>(n_, -1));

int ans = 0;

for (int y = 0; y < m_; ++y)

for (int x = 0; x < n_; ++x)

ans = max(ans, dfs(matrix, x, y));

return ans;

}

private:

int dfs(const vector<vector<int>>& mat, int x, int y) {

if (dp_[y][x] != -1) return dp_[y][x];

static int dirs[] = {0, -1, 0, 1, 0};

dp_[y][x] = 1;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || ty < 0 || tx >= n_ || ty >= m_ || mat[ty][tx] <= mat[y][x])

continue;

dp_[y][x] = max(dp_[y][x], 1 + dfs(mat, tx, ty));

}

return dp_[y][x];

}

int m_;

int n_;

// dp[i][j]: max length start from (j, i)

vector<vector<int>> dp_;

};

Solution2: DP

Time complexity: O(mn*log(mn))

Space complexity: O(mn)

// Author: Huahua

// Running time: 63 ms

class Solution {

public:

int longestIncreasingPath(vector<vector<int>>& matrix) {

if (matrix.empty()) return 0;

int m = matrix.size();

int n = matrix[0].size();

vector<vector<int>> dp(m, vector<int>(n, 1));

int ans = 0;

vector<pair<int, pair<int, int>>> cells;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

cells.push_back({matrix[y][x], {x, y}});

sort(cells.rbegin(), cells.rend());

vector<int> dirs {0, 1, 0, -1, 0};

for (const auto& cell : cells) {

int x = cell.second.first;

int y = cell.second.second;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || tx >= n || ty < 0 || ty >= m) continue;

if (matrix[ty][tx] <= matrix[y][x]) continue;

dp[y][x] = max(dp[y][x], 1 + dp[ty][tx]);

}

ans = max(ans, dp[y][x]);

}

return ans;

}

};

花花酱 LeetCode 830. Positions of Large Groups

By zxi on May 13, 2018

Problem

In a string S of lowercase letters, these letters form consecutive groups of the same character.

For example, a string like S = "abbxxxxzyy" has the groups "a", "bb", "xxxx", "z" and "yy".

Call a group large if it has 3 or more characters. We would like the starting and ending positions of every large group.

The final answer should be in lexicographic order.

Example 1:

Input: "abbxxxxzzy"
Output: [[3,6]]
Explanation: "xxxx" is the single large group with starting 3 and ending positions 6.

Example 2:

Input: "abc"
Output: []
Explanation: We have "a","b" and "c" but no large group.

Example 3:

Input: "abcdddeeeeaabbbcd"
Output: [[3,5],[6,9],[12,14]]

Note: 1 <= S.length <= 1000

Solution: Brute Force

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 18 ms

class Solution {

public:

vector<vector<int>> largeGroupPositions(string S) {

constexpr int kLargeGroupSize = 3;

const int n = S.size();

vector<vector<int>> ans;

int c = 0;

for (int i = 0; i <= n; ++i, ++c) {

if (i == n || S[i] != S[i - 1]) {

if (c >= kLargeGroupSize) ans.push_back({i - c, i - 1});

c = 0;

}

return ans;

}

};

花花酱 LeetCode 832. Flipping an Image

By zxi on May 13, 2018

Problem

Given a binary matrix A, we want to flip the image horizontally, then invert it, and return the resulting image.

To flip an image horizontally means that each row of the image is reversed. For example, flipping [1, 1, 0] horizontally results in [0, 1, 1].

To invert an image means that each 0 is replaced by 1, and each 1 is replaced by 0. For example, inverting [0, 1, 1] results in [1, 0, 0].

Example 1:

Input: [[1,1,0],[1,0,1],[0,0,0]]
Output: [[1,0,0],[0,1,0],[1,1,1]]
Explanation: First reverse each row: [[0,1,1],[1,0,1],[0,0,0]].
Then, invert the image: [[1,0,0],[0,1,0],[1,1,1]]

Example 2:

Input: [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
Output: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
Explanation: First reverse each row: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]].
Then invert the image: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]

Notes:

1 <= A.length = A[0].length <= 20
0 <= A[i][j] <= 1

Solution 1: Brute Force

Time complexity: O(m*n)

Space complexity: O(m*n)

C++

// Author: Huahua

// Running time: 15 ms

class Solution {

public:

vector<vector<int>> flipAndInvertImage(vector<vector<int>>& A) {

auto B = A;

int m = A.size();

int n = A[0].size();

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

B[i][j] = 1 - A[i][n - j - 1];

return B;

}

};

花花酱 LeetCode 810. Chalkboard XOR Game

By zxi on May 2, 2018

Problem

We are given non-negative integers nums[i] which are written on a chalkboard. Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become 0, then that player loses. (Also, we’ll say the bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is 0.)

Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to 0, then that player wins.

Return True if and only if Alice wins the game, assuming both players play optimally.

Example:
Input: nums = [1, 1, 2]
Output: false
Explanation: 
Alice has two choices: erase 1 or erase 2. 
If she erases 1, the nums array becomes [1, 2]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose. 
If Alice erases 2 first, now nums becomes [1, 1]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.

Notes:

1 <= N <= 1000.
0 <= nums[i] <= 2^16.

Solution: Math

Time complexity: O(n)

Space complexity: O(1)

// Author: Huahua

// Running time: 15 ms

class Solution {

public:

bool xorGame(vector<int>& nums) {

if (nums.size() % 2 == 0) return true;

int x = 0;

for (int num : nums) x ^= num;

return x == 0;

}

};

Huahua's Tech Road

花花酱 LeetCode 841. Keys and Rooms

Problem

Solution: DFS

花花酱 LeetCode 329. Longest Increasing Path in a Matrix

Problem

Solution1: DFS + Memorization

Solution2: DP

花花酱 LeetCode 830. Positions of Large Groups

Problem

Solution: Brute Force

花花酱 LeetCode 832. Flipping an Image

Problem

Solution 1: Brute Force

花花酱 LeetCode 810. Chalkboard XOR Game

Problem

Solution: Math