花花酱 LeetCode 378. Kth Smallest Element in a Sorted Matrix

By zxi on February 20, 2018

题目大意：给你一个矩阵，每行每列各自排序。找出矩阵中第K小的元素。

Given a n x n matrix where each of the rows and columns are sorted in ascending order, find the kth smallest element in the matrix.

Note that it is the kth smallest element in the sorted order, not the kth distinct element.

Example:

matrix = [

[ 1, 5, 9],

[10, 11, 13],

[12, 13, 15]

k = 8,

return 13.

Note:
You may assume k is always valid, 1 ≤ k ≤ n².

Solution 1: Binary Search

Find the smallest x, such that there are k elements that are smaller or equal to x.

Time complexity: O(nlogn*log(max – min))

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 24 ms (beats 97.12%)

class Solution {

public:

int kthSmallest(vector<vector<int>>& matrix, int k) {

const int n = matrix.size();

long l = matrix[0][0];

long r = matrix[n - 1][n - 1] + 1;

while (l < r) {

long m = l + (r - l) / 2;

int total = 0;

int s = n;

for (const auto& row : matrix)

total += (s = distance(begin(row), upper_bound(begin(row), begin(row) + s, m)));

if (total >= k)

r = m;

else

l = m + 1;

}

return l;

}

};

花花酱 LeetCode 786. K-th Smallest Prime Fraction

By zxi on February 20, 2018

题目大意：给你一些互质数字，求出它们组成的分数中第K小的分数。

A sorted list A contains 1, plus some number of primes. Then, for every p < q in the list, we consider the fraction p/q.

What is the K-th smallest fraction considered? Return your answer as an array of ints, where answer[0] = p and answer[1] = q.

Examples:

Input: A = [1, 2, 3, 5], K = 3

Output: [2, 5]

Explanation:

The fractions to be considered in sorted order are:

1/5, 1/3, 2/5, 1/2, 3/5, 2/3.

The third fraction is 2/5.

Input: A = [1, 7], K = 1

Output: [1, 7]

Note:

A will have length between 2 and 2000.
Each A[i] will be between 1 and 30000.
K will be between 1 and A.length * (A.length + 1) / 2.

Solution 1: Binary Search

Binary search m, 0 < m < 1, such that there are exact k pairs of (i, j) that A[i] / A[j] < m

Time complexity: O(n*C) C <= 31

C++

// Author: Huahua

// Running time: 13 ms

class Solution {

public:

vector<int> kthSmallestPrimeFraction(vector<int>& A, int K) {

const int n = A.size();

double l = 0;

double r = 1.0;

while (l < r) {

double m = (l + r) / 2;

double max_f = 0.0;

int total = 0;

int p, q = 0;

for (int i = 0, j = 1; i < n - 1; ++i) {

while (j < n && A[i] > m * A[j]) ++j;

if (n == j) break;

total += (n - j);

const double f = static_cast<double>(A[i]) / A[j];

if (f > max_f) {

p = i;

q = j;

max_f = f;

}

if (total == K)

return {A[p], A[q]};

else if (total > K)

r = m;

else

l = m;

}

return {};

}

};

Java

// Author: Huahua

// Running time: 16 ms

class Solution {

public int[] kthSmallestPrimeFraction(int[] A, int K) {

final int n = A.length;

double l = 0;

double r = 1.0;

while (l < r) {

double m = (l + r) / 2;

double max_f = 0.0;

int total = 0;

int p = 0;

int q = 0;

for (int i = 0, j = 1; i < n - 1; ++i) {

while (j < n && A[i] > m * A[j]) ++j;

if (n == j) break;

total += (n - j);

final double f = (double)A[i] / A[j];

if (f > max_f) {

p = i;

q = j;

max_f = f;

}

if (total == K)

return new int[]{A[p], A[q]};

else if (total > K)

r = m;

else

l = m;

}

return new int[] {};

}

Python3

"""

Author: Huahua

Running time: 172 ms

"""

class Solution:

def kthSmallestPrimeFraction(self, A, K):

n = len(A)

l = 0.0

r = 1.0

while l < r:

m = (l + r) / 2

max_f = 0.0

total = 0

j = 1

for i in range(n - 1):

while j < n and A[i] > m * A[j]: j += 1

if j == n: break

total += n - j

f = A[i] / A[j]

if f > max_f:

p, q, max_f = i, j, f

if total == K:

return [A[p], A[q]]

elif total > K:

r = m

else:

l = m

return []

Related Problems:

花花酱 LeetCode 784. Letter Case Permutation

By zxi on February 20, 2018

题目大意：给你一个字符串，每个字母可以变成大写也可以变成小写。让你输出所有可能字符串。

Given a string S, we can transform every letter individually to be lowercase or uppercase to create another string. Return a list of all possible strings we could create.

Examples:

Input: S = "a1b2"

Output: ["a1b2", "a1B2", "A1b2", "A1B2"]

Input: S = "3z4"

Output: ["3z4", "3Z4"]

Input: S = "12345"

Output: ["12345"]

Note:

S will be a string with length at most 12.
S will consist only of letters or digits.

Solution 1: DFS

Time complexity: O(n*2^l), l = # of letters in the string

Space complexity: O(n) + O(n*2^l)

C++

// Author: Huahua

// Running time: 7 ms

class Solution {

public:

vector<string> letterCasePermutation(string S) {

vector<string> ans;

dfs(S, 0, ans);

return ans;

}

private:

void dfs(string& S, int s, vector<string>& ans) {

if (s == S.length()) {

ans.push_back(S);

return;

}

dfs(S, s + 1, ans);

if (!isalpha(S[s])) return;

S[s] ^= (1 << 5);

dfs(S, s + 1, ans);

S[s] ^= (1 << 5);

}

};

Java

// Author: Huahua

// Running time: 8 ms

class Solution {

public List<String> letterCasePermutation(String S) {

List<String> ans = new ArrayList<>();

dfs(S.toCharArray(), 0, ans);

return ans;

}

private void dfs(char[] S, int i, List<String> ans) {

if (i == S.length) {

ans.add(new String(S));

return;

}

dfs(S, i + 1, ans);

if (!Character.isLetter(S[i])) return;

S[i] ^= 1 << 5;

dfs(S, i + 1, ans);

S[i] ^= 1 << 5;

}

Python 3

"""

Author: Huahua

Running time: 92 ms

"""

class Solution:

def letterCasePermutation(self, S):

ans = []

def dfs(S, i, n):

if i == n:

ans.append(''.join(S))

return

dfs(S, i + 1, n)

if not S[i].isalpha(): return

S[i] = chr(ord(S[i]) ^ (1<<5))

dfs(S, i + 1, n)

S[i] = chr(ord(S[i]) ^ (1<<5))

dfs(list(S), 0, len(S))

return ans

花花酱 LeetCode 783. Minimum Distance Between BST Nodes

By zxi on February 10, 2018

Given a Binary Search Tree (BST) with the root node root, return the minimum difference between the values of any two different nodes in the tree.

Example :

Input: root = [4,2,6,1,3,null,null]

Output: 1

Explanation:

Note that root is a TreeNode object, not an array.

The given tree [4,2,6,1,3,null,null] is represented by the following diagram:

/ \

2 6

/ \

1 3

while the minimum difference in this tree is 1, it occurs between node 1 and node 2, also between node 3 and node 2.

Note:

The size of the BST will be between 2 and 100.
The BST is always valid, each node’s value is an integer, and each node’s value is different.

Solution 1: In order traversal

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 783

class Solution {

public:

int minDiffInBST(TreeNode* root) {

min_diff_ = INT_MAX;

prev_ = nullptr;

minDiff(root);

return min_diff_;

}

private:

int min_diff_;

int* prev_;

void minDiff(TreeNode* root) {

if (root == nullptr) return;

minDiff(root->left);

if (prev_ != nullptr)

min_diff_ = min(min_diff_, abs(root->val - *prev_));

prev_ = &root->val;

minDiff(root->right);

}

};

Related Problems:

花花酱 LeetCode 530. Minimum Absolute Difference in BST

花花酱 Time/Space Complexity of Recursion Functions SP4

By zxi on February 7, 2018

How to analyze the time and space complexity of a recursion function?

如何分析一个递归函数的时间/空间复杂度？

We can answer that using master theorem or induction in most of the cases.

在大部分时候我们可以使用主方法和数学归纳法来进行解答。

First of all, we need to write down the recursion relation of a function.

首先我们要写出一个函数的递归表达式。

def func(n):

if n < 0: return 1

return func(n/2) + func(n/2)

Let’s use T(n) to denote the running time of func with input size of n.

让我们用T(n)来表示func函数在输入规模为n的运行时间。

Then we have：

那么我们有：

T(n) = 2*T(n/2) + O(1)

a = 2, b = 2, c_crit = logb(a) = 1, f(n) = n^c, c = 0.

c < c_crit, apply master theorem case 1:

根据主方法第一条我们得到

T(n) = Θ(n^c_crit) = Θ(n)

Let’s look at another example:

def func(n):

if n < 0: return 1

s = 0

for i in range(n):

s += i

return s + func(n/2) + func(n/2)

T(n) = 2*T(n/2) + O(n)

a = 2, b = 2, c_crit = logb(a) = 1, f(n) = n^c, c = 1,

c = c_crit, apply master theorem case 2:

根据主方法第二条我们得到

T(n) =Θ(n^c_crit * (logn)^1)) = Θ(nlogn)

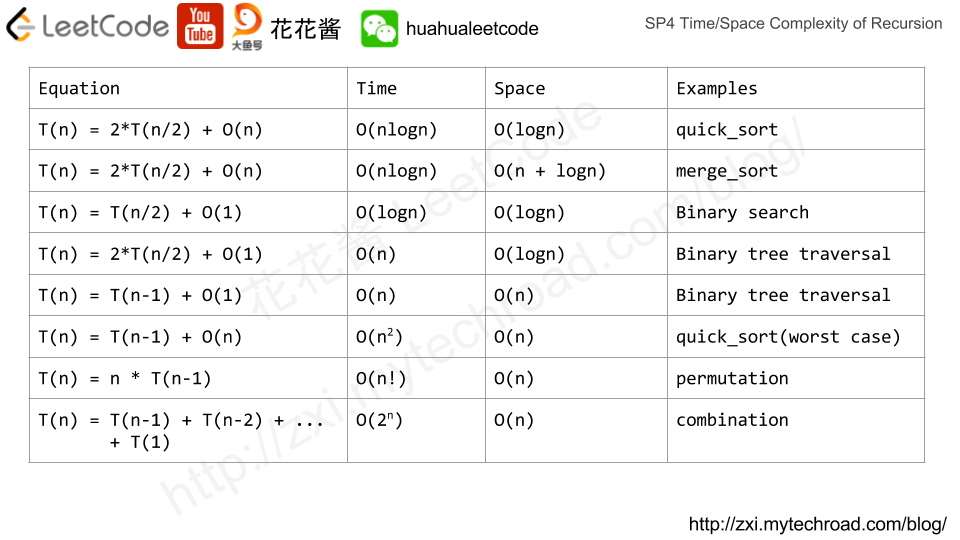
Cheatsheet

Equation	Time	Space	Examples
T(n) = 2*T(n/2) + O(n)	O(nlogn)	O(logn)	quick_sort
T(n) = 2*T(n/2) + O(n)	O(nlogn)	O(n + logn)	merge_sort
T(n) = T(n/2) + O(1)	O(logn)	O(logn)	Binary search
T(n) = 2*T(n/2) + O(1)	O(n)	O(logn)	Binary tree traversal
T(n) = T(n-1) + O(1)	O(n)	O(n)	Binary tree traversal
T(n) = T(n-1) + O(n)	O(n^2)	O(n)	quick_sort(worst case)
T(n) = n * T(n-1)	O(n!)	O(n)	permutation
T(n) = T(n-1)+T(n-2)+…+T(1)	O(2^n)	O(n)	combination

For recursion with memorization:

Time complexity: |# of subproblems| * |exclusive running time of a subproblem|

Example 1:

def fib(n):

if n < 1: return 1

if m[n]: return m[n]

m[n] = fib(n - 1) + fib(n - 2)

return m[n]

To solve fib(n), there are n subproblems fib(0), fib(1), …, fib(n)

each sub problem takes O(1) to solve

Time complexity: O(n)

Space complexity: O(n) + O(n) * O(1) = O(n)

Example 2:

LC 741 Cherry Pickup

dp(x1, y1, x2):

if min(x1, y1, x2) < 0: return 0

if m[x1][y1][x2]: return m[x1][y1][x2]

ans = max(dp(x1 - 1, y1, x2 - 1),

dp(x1, y1 - 1, x2),

dp(x1, y1 - 1, x2 - 1),

dp(x1 - 1, y1, x2))

m[x1][y1][x2] = ans

return m[x1][y1][x2]

To solve dp(n, n, n), there are n^3 subproblems

each subproblem takes O(1) to solve

Max recursion depth O(n)

Time complexity: O(n^3) * O(1) = O(n^3)

Space complexity: O(n^3) + O(n) * O(1) = O(n^3)

Example 3:

LC 312: Burst Balloon

dp(i, j):

if m[i][j]: return m[i][j]

for k in range(i, j + 1):

ans = max(ans, dp(i, k - 1) + C + dp(k + 1, j))

m[i][j] = ans

return m[i][j]

To solve dp(0, n), there are n^2 subproblems dp(0, 0), dp(0, 1), …, dp(n-1, n)

each subproblem takes O(n) to solve

Max recursion depth O(n)

Time complexity: O(n^2) * O(n) = O(n^3)

Space complexity: O(n^2) + O(n) * O(1) = O(n^2)

Slides:

Huahua's Tech Road

花花酱 LeetCode 378. Kth Smallest Element in a Sorted Matrix

Solution 1: Binary Search

花花酱 LeetCode 786. K-th Smallest Prime Fraction

Solution 1: Binary Search

C++

Java

Python3

花花酱 LeetCode 784. Letter Case Permutation

Solution 1: DFS

C++

Java

Python 3

花花酱 LeetCode 783. Minimum Distance Between BST Nodes

花花酱 Time/Space Complexity of Recursion Functions SP4