Huahua’s Tech Road

花花酱 LeetCode 2304. Minimum Path Cost in a Grid

By zxi on June 14, 2022

You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

Example 1:

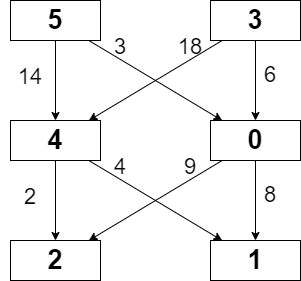
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 50
grid consists of distinct integers from 0 to m * n - 1.
moveCost.length == m * n
moveCost[i].length == n
1 <= moveCost[i][j] <= 100

Solution: DP

Let dp[i][j] := min cost to reach grid[i][j] from the first row.

dp[i][j] = min{grid[i][j] + dp[i – 1][k] + moveCost[grid[i – 1][k]][j]} 0 <= k < n

For each node, try all possible nodes from the previous row.

Time complexity: O(m*n²)
Space complexity: O(m*n) -> O(n)

C++

// Author: Huahua

class Solution {

public:

int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {

const int m = grid.size();

const int n = grid[0].size();

vector<vector<int>> dp(m, vector<int>(n, INT_MAX));

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

for (int k = 0; k < n; ++k)

dp[i][j] = min(dp[i][j], grid[i][j] +

(i ? dp[i - 1][k] + moveCost[grid[i - 1][k]][j] : 0));

return *min_element(begin(dp[m - 1]), end(dp[m - 1]));

}

};

花花酱 LeetCode 2303. Calculate Amount Paid in Taxes

By zxi on June 14, 2022

You are given a 0-indexed 2D integer array brackets where brackets[i] = [upper_i, percent_i] means that the i^th tax bracket has an upper bound of upper_i and is taxed at a rate of percent_i. The brackets are sorted by upper bound (i.e. upper_i-1 < upper_i for 0 < i < brackets.length).

Tax is calculated as follows:

The first upper₀ dollars earned are taxed at a rate of percent₀.
The next upper₁ - upper₀ dollars earned are taxed at a rate of percent₁.
The next upper₂ - upper₁ dollars earned are taxed at a rate of percent₂.
And so on.

You are given an integer income representing the amount of money you earned. Return the amount of money that you have to pay in taxes. Answers within 10^-5 of the actual answer will be accepted.

Example 1:

Input: brackets = [[3,50],[7,10],[12,25]], income = 10
Output: 2.65000
Explanation:
The first 3 dollars you earn are taxed at 50%. You have to pay $3 * 50% = $1.50 dollars in taxes.
The next 7 - 3 = 4 dollars you earn are taxed at 10%. You have to pay $4 * 10% = $0.40 dollars in taxes.
The final 10 - 7 = 3 dollars you earn are taxed at 25%. You have to pay $3 * 25% = $0.75 dollars in taxes.
You have to pay a total of $1.50 + $0.40 + $0.75 = $2.65 dollars in taxes.

Example 2:

Input: brackets = [[1,0],[4,25],[5,50]], income = 2
Output: 0.25000
Explanation:
The first dollar you earn is taxed at 0%. You have to pay $1 * 0% = $0 dollars in taxes.
The second dollar you earn is taxed at 25%. You have to pay $1 * 25% = $0.25 dollars in taxes.
You have to pay a total of $0 + $0.25 = $0.25 dollars in taxes.

Example 3:

Input: brackets = [[2,50]], income = 0
Output: 0.00000
Explanation:
You have no income to tax, so you have to pay a total of $0 dollars in taxes.

Constraints:

1 <= brackets.length <= 100
1 <= upper_i <= 1000
0 <= percent_i <= 100
0 <= income <= 1000
upper_i is sorted in ascending order.
All the values of upper_i are unique.
The upper bound of the last tax bracket is greater than or equal to income.

Solution: Follow the rules

“Nothing is certain except death and taxes” – Benjamin Franklin

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

double calculateTax(vector<vector<int>>& A, int income) {

double ans = 0;

for (int i = 0; i < A.size(); ++i) {

ans += (min(income, A[i][0]) - (i ? A[i-1][0] : 0)) * A[i][1] / 100.0;

if (A[i][0] >= income) break;

}

return ans;

}

};

花花酱 LeetCode 2270. Number of Ways to Split Array

By zxi on May 15, 2022

You are given a 0-indexed integer array nums of length n.

nums contains a valid split at index i if the following are true:

The sum of the first i + 1 elements is greater than or equal to the sum of the last n - i - 1 elements.
There is at least one element to the right of i. That is, 0 <= i < n - 1.

Return the number of valid splits in nums.

Example 1:

Input: nums = [10,4,-8,7]
Output: 2
Explanation: 
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is [10], and its sum is 10. The second part is [4,-8,7], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is [10,4], and its sum is 14. The second part is [-8,7], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is [10,4,-8], and its sum is 6. The second part is [7], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.

Example 2:

Input: nums = [2,3,1,0]
Output: 2
Explanation: 
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is [2,3], and its sum is 5. The second part is [1,0], and its sum is 1. Since 5 >= 1, i = 1 is a valid split. 
- Split nums at index 2. Then, the first part is [2,3,1], and its sum is 6. The second part is [0], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.

Constraints:

2 <= nums.length <= 10⁵
-10⁵ <= nums[i] <= 10⁵

Solution: Prefix/Suffix Sum

Note: sum can be greater than 2^31, use long!

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int waysToSplitArray(vector<int>& A) {

int ans = 0;

for (long i = 0, l = 0, r = accumulate(begin(A), end(A), 0l); i < A.size() - 1; ++i)

ans += (l += A[i]) >= (r -= A[i]);

return ans;

}

};

花花酱 LeetCode 2269. Find the K-Beauty of a Number

By zxi on May 15, 2022

The k-beauty of an integer num is defined as the number of substrings of num when it is read as a string that meet the following conditions:

It has a length of k.
It is a divisor of num.

Given integers num and k, return the k-beauty of num.

Note:

Leading zeros are allowed.
0 is not a divisor of any value.

A substring is a contiguous sequence of characters in a string.

Example 1:

Input: num = 240, k = 2
Output: 2
Explanation: The following are the substrings of num of length k:
- "24" from "240": 24 is a divisor of 240.
- "40" from "240": 40 is a divisor of 240.
Therefore, the k-beauty is 2.

Example 2:

Input: num = 430043, k = 2
Output: 2
Explanation: The following are the substrings of num of length k:
- "43" from "430043": 43 is a divisor of 430043.
- "30" from "430043": 30 is not a divisor of 430043.
- "00" from "430043": 0 is not a divisor of 430043.
- "04" from "430043": 4 is not a divisor of 430043.
- "43" from "430043": 43 is a divisor of 430043.
Therefore, the k-beauty is 2.

Constraints:

1 <= num <= 10⁹
1 <= k <= num.length (taking num as a string)

Solution: Substring

Note: the substring can be 0, e.g. “00”

Time complexity: O((l-k)*k)
Space complexity: O(l + k) -> O(1)

C++

// Author: Huahua

class Solution {

public:

int divisorSubstrings(int num, int k) {

string s = to_string(num);

int ans = 0;

for (int i = 0; i <= s.length() - k; ++i) {

const int t = stoi(s.substr(i, k));

ans += t && (num % t == 0);

}

return ans;

}

};

花花酱 LeetCode 2267. Check if There Is a Valid Parentheses String Path

By zxi on May 10, 2022

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

It is ().
It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
It can be written as (A), where A is a valid parentheses string.

You are given an m x n matrix of parentheses grid. A valid parentheses string path in the grid is a path satisfying all of the following conditions:

The path starts from the upper left cell (0, 0).
The path ends at the bottom-right cell (m - 1, n - 1).
The path only ever moves down or right.
The resulting parentheses string formed by the path is valid.

Return true if there exists a valid parentheses string path in the grid. Otherwise, return false.

Example 1:

Input: grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
Output: true
Explanation: The above diagram shows two possible paths that form valid parentheses strings.
The first path shown results in the valid parentheses string "()(())".
The second path shown results in the valid parentheses string "((()))".
Note that there may be other valid parentheses string paths.

Example 2:

Input: grid = [[")",")"],["(","("]]
Output: false
Explanation: The two possible paths form the parentheses strings "))(" and ")((". Since neither of them are valid parentheses strings, we return false.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
grid[i][j] is either '(' or ')'.

Solution: DP

Let dp(i, j, b) denote whether there is a path from (i,j) to (m-1, n-1) given b open parentheses.
if we are at (m – 1, n – 1) and b == 0 then we found a valid path.
dp(i, j, b) = dp(i + 1, j, b’) or dp(i, j + 1, b’) where b’ = b + 1 if grid[i][j] == ‘(‘ else -1

Time complexity: O(m*n*(m + n))
Space complexity: O(m*n*(m + n))

Python3

# Author: Huahua

class Solution:

def hasValidPath(self, grid: List[List[str]]) -> bool:

m, n = len(grid), len(grid[0])

@cache

def dp(i: int, j: int, b: int) -> bool:

if b < 0 or i == m or j == n: return False

b += 1 if grid[i][j] == '(' else -1

if i == m - 1 and j == n - 1 and b == 0: return True

return dp(i + 1, j, b) or dp(i, j + 1, b)

return dp(0, 0, 0)

Huahua's Tech Road

花花酱 LeetCode 2304. Minimum Path Cost in a Grid

Solution: DP

C++

花花酱 LeetCode 2303. Calculate Amount Paid in Taxes

Solution: Follow the rules

C++

花花酱 LeetCode 2270. Number of Ways to Split Array

Solution: Prefix/Suffix Sum

C++

花花酱 LeetCode 2269. Find the K-Beauty of a Number

Solution: Substring

C++

花花酱 LeetCode 2267. Check if There Is a Valid Parentheses String Path

Solution: DP

Python3