Huahua’s Tech Road

花花酱 LeetCode 675. Cut Off Trees for Golf Event

By zxi on September 14, 2017

https://leetcode.com/problems/cut-off-trees-for-golf-event/

Problem:

You are asked to cut off trees in a forest for a golf event. The forest is represented as a non-negative 2D map, in this map:

0 represents the obstacle can’t be reached.
1 represents the ground can be walked through.
The place with number bigger than 1 represents a tree can be walked through, and this positive number represents the tree’s height.

You are asked to cut off all the trees in this forest in the order of tree’s height – always cut off the tree with lowest height first. And after cutting, the original place has the tree will become a grass (value 1).

You will start from the point (0, 0) and you should output the minimum steps you need to walk to cut off all the trees. If you can’t cut off all the trees, output -1 in that situation.

You are guaranteed that no two trees have the same height and there is at least one tree needs to be cut off.

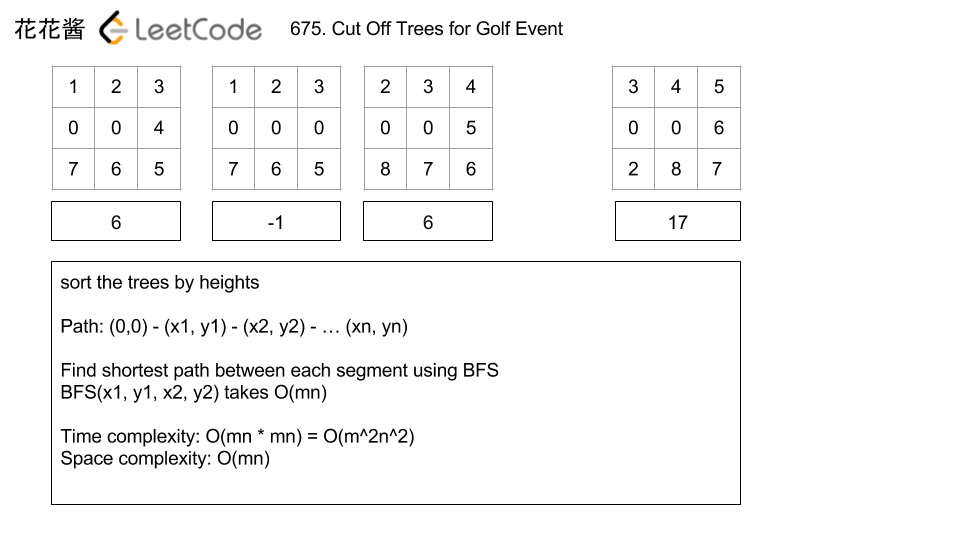
Example 1:

Input:

[

[1,2,3],

[0,0,4],

[7,6,5]

]

Output: 6

Example 2:

Input:

[

[1,2,3],

[0,0,0],

[7,6,5]

]

Output: -1

Example 3:

Input:

[

[2,3,4],

[0,0,5],

[8,7,6]

]

Output: 6

Explanation: You started from the point (0,0) and you can cut off the tree in (0,0) directly without walking.

Hint: size of the given matrix will not exceed 50×50.

Idea:

Greedy + Shortest path

Identify and sort the trees by its heights, then find shortest paths between

0,0 to tree[1]
tree[1] to tree[2]
…
tree[n-1] to tree[n]

Time complexity: O(m^2n^2)

Space complexity: O(mn)

Solution:

// Author: Huahua

// Running time: 282 ms

class Solution {

public:

int cutOffTree(vector<vector<int>>& forest) {

m_ = forest.size();

n_ = forest[0].size();

// {height, x, y}

vector<tuple<int,int,int>> trees;

for (int y = 0; y < m_; ++y)

for (int x = 0; x < n_; ++x)

if (forest[y][x] > 1)

trees.emplace_back(forest[y][x], x, y);

// sort trees by height

sort(trees.begin(), trees.end());

int sx = 0;

int sy = 0;

int total_steps = 0;

// Move from current position to next tree to cut

for (int i = 0; i < trees.size(); ++i) {

int tx = get<1>(trees[i]);

int ty = get<2>(trees[i]);

int steps = BFS(forest, sx, sy, tx, ty);

if (steps == INT_MAX) return -1;

// Cut the tree, not necessary

forest[ty][tx] = 1;

total_steps += steps;

sx = tx;

sy = ty;

}

return total_steps;

}

private:

// min steps to go from (sx,sy) to (tx,ty) based on current map

// INT_MAX means not reachable

int BFS(const vector<vector<int>>& forest,

int sx, int sy,

int tx, int ty) {

static int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

auto visited = vector<vector<int>>(m_, vector<int>(n_, 0));

// {x, y}

queue<pair<int,int>> q;

q.emplace(sx, sy);

int steps = 0;

while (!q.empty()) {

int new_nodes = q.size();

while (new_nodes--) {

auto node = q.front();

q.pop();

const int cx = node.first;

const int cy = node.second;

// Found the shortest path

if (cx == tx && cy == ty)

return steps;

for (int i = 0; i < 4; ++i) {

const int x = cx + dirs[i][0];

const int y = cy + dirs[i][1];

// Out of bound or unwalkable

if (x < 0 || x == n_

|| y < 0 || y == m_

|| !forest[y][x]

|| visited[y][x]) continue;

// Mark x, y as visited

visited[y][x] = 1;

q.emplace(x, y);

}

++steps;

}

// Impossible to reach

return INT_MAX;

}

int m_;

int n_;

};

花花酱 LeetCode 460. LFU Cache

By zxi on September 14, 2017

Problem:

Design and implement a data structure for Least Frequently Used (LFU) cache. It should support the following operations: get and put.

get(key) – Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.
put(key, value) – Set or insert the value if the key is not already present. When the cache reaches its capacity, it should invalidate the least frequently used item before inserting a new item. For the purpose of this problem, when there is a tie (i.e., two or more keys that have the same frequency), the least recently used key would be evicted.

Follow up:
Could you do both operations in O(1) time complexity?

Example:

LFUCache cache = new LFUCache( 2 /* capacity */ );

cache.put(1, 1);

cache.put(2, 2);

cache.get(1); // returns 1

cache.put(3, 3); // evicts key 2

cache.get(2); // returns -1 (not found)

cache.get(3); // returns 3.

cache.put(4, 4); // evicts key 1.

cache.get(1); // returns -1 (not found)

cache.get(3); // returns 3

cache.get(4); // returns 4

Idea:

Hashtable + balanced search tree

Hashtable + double linked list

Solution 1: O(logc) c is the capacity

// Author: Huahua

// Running time: 99 ms

struct CacheNode {

int key;

int value;

int freq;

long tick;

// Defines the order, smaller one will be evicted first

bool operator <(const CacheNode& rhs) const {

if (freq < rhs.freq) return true;

if (freq == rhs.freq) return tick < rhs.tick;

return false;

}

};

class LFUCache {

public:

LFUCache(int capacity):capacity_(capacity), tick_(0) {}

int get(int key) {

auto it = m_.find(key);

if (it == m_.cend()) return -1;

int value = it->second.value;

touch(it->second);

return value;

}

void put(int key, int value) {

if (capacity_ == 0) return;

auto it = m_.find(key);

if (it != m_.cend()) {

// Key exists, update value and touch

it->second.value = value;

touch(it->second);

return;

}

if (m_.size() == capacity_) {

// Remove the first node in cache

const CacheNode& node = *cache_.cbegin();

m_.erase(node.key);

cache_.erase(node);

}

CacheNode node{key, value, 1, ++tick_};

m_[node.key] = node;

cache_.insert(node);

}

private:

void touch(CacheNode& node) {

cache_.erase(node); // log(capacity)

++node.freq;

node.tick = ++tick_;

cache_.insert(node); // log(capacity)

}

long tick_;

int capacity_;

unordered_map<int, CacheNode> m_;

set<CacheNode> cache_;

};

Solution 2: O(1)

// Author: Huahua

// Running time: 89 ms (beats 96.3%)

struct CacheNode {

int key;

int value;

int freq;

// pointer to the node in the list

list<int>::const_iterator it;

};

class LFUCache {

public:

LFUCache(int capacity): capacity_(capacity), min_freq_(0) {}

int get(int key) {

auto it = n_.find(key);

if (it == n_.cend()) return -1;

touch(it->second);

return it->second.value;

}

void put(int key, int value) {

if (capacity_ == 0) return;

auto it = n_.find(key);

if (it != n_.cend()) {

// Key already exists, update the value and touch it

it->second.value = value;

touch(it->second);

return;

}

if (n_.size() == capacity_) {

// No capacity, need to remove one entry that

// 1. has the lowest freq

// 2. least recently used if there are multiple ones

// Step 1: remove the element from min_freq_ list

const int key_to_evict = l_[min_freq_].back();

l_[min_freq_].pop_back();

// Step 2: remove the key from cache

n_.erase(key_to_evict);

}

// We know new item has freq of 1, thus set min_freq to 1

const int freq = 1;

min_freq_ = freq;

// Add the key to the freq list

l_[freq].push_front(key);

// Create a new node

n_[key] = {key, value, freq, l_[freq].cbegin()};

}

private:

void touch(CacheNode& node) {

// Step 1: update the frequency

const int prev_freq = node.freq;

const int freq = ++(node.freq);

// Step 2: remove the entry from old freq list

l_[prev_freq].erase(node.it);

if (l_[prev_freq].empty() && prev_freq == min_freq_) {

// Delete the list

l_.erase(prev_freq);

// Increase the min freq

++min_freq_;

}

// Step 4: insert the key into the front of the new freq list

l_[freq].push_front(node.key);

// Step 5: update the pointer

node.it = l_[freq].cbegin();

}

int capacity_;

int min_freq_;

// key -> CacheNode

unordered_map<int, CacheNode> n_;

// freq -> keys with freq

unordered_map<int, list<int>> l_;

};

花花酱 LeetCode 451. Sort Characters By Frequency

By zxi on September 13, 2017

Problem:

Given a string, sort it in decreasing order based on the frequency of characters.

Example 1:

Input:
“tree”

Output:
“eert”

Explanation:
‘e’ appears twice while ‘r’ and ‘t’ both appear once.
So ‘e’ must appear before both ‘r’ and ‘t’. Therefore “eetr” is also a valid answer.
Example 2:

Input:
“cccaaa”

Output:
“cccaaa”

Explanation:
Both ‘c’ and ‘a’ appear three times, so “aaaccc” is also a valid answer.
Note that “cacaca” is incorrect, as the same characters must be together.
Example 3:

Input:
“Aabb”

Output:
“bbAa”

Explanation:
“bbaA” is also a valid answer, but “Aabb” is incorrect.
Note that ‘A’ and ‘a’ are treated as two different characters.

Idea:

Counting sort

Solution 1:

Sort the string based on element frequency

// Author: Huahua

// Running time: 289 ms

class Solution {

public:

string frequencySort(string& s) {

array<int, 128> f{0};

for(char c:s) ++f[c];

sort(s.begin(), s.end(), [&f] (char a, char b) {

return f[a] > f[b] || (f[a] == f[b] && a > b);

});

return s;

}

};

// Author: Huahua

// Running time: 139 ms

class Solution {

public:

string frequencySort(string& s) {

map<char, int> f;

for(char c:s) ++f[c];

sort(s.begin(), s.end(), [&f] (char a, char b) {

return f[a] > f[b] || (f[a] == f[b] && a > b);

});

return s;

}

};

// Author: Huahua

// Running time: 29 ms

class Solution {

public:

string frequencySort(string& s) {

array<int, 128> f{0};

for(char c:s) ++f[c];

sort(s.begin(), s.end(), [&f] (char a, char b) {

return f[a] > f[b] || (f[a] == f[b] && a > b);

});

return s;

}

};

Solution 2:

Counting sort

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

string frequencySort(const string& s) {

vector<int> f(128, 0);

for(char c:s) ++f[c];

vector<pair<int,char>> v;

for (int i = 0; i < 128; ++i) {

if (f[i] > 0) v.emplace_back(f[i], i);

}

sort(v.rbegin(), v.rend());

string ans;

for(const auto& kv : v) {

ans.append(kv.first, kv.second);

}

return ans;

}

};

花花酱 LeetCode 332. Reconstruct Itinerary

By zxi on September 12, 2017

Problem:

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
All airports are represented by three capital letters (IATA code).
You may assume all tickets form at least one valid itinerary.

Example 1:
tickets = [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Return ["JFK", "MUC", "LHR", "SFO", "SJC"].

Example 2:
tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Return ["JFK","ATL","JFK","SFO","ATL","SFO"].
Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"]. But it is larger in lexical order.

Idea:

Convert the graph to a tree and do post-order traversal

Solution:

// Author: Huahua

// Running time: 13 ms

class Solution {

public:

vector<string> findItinerary(vector<pair<string, string>> tickets) {

route_.clear();

trips_.clear();

for(const auto& pair : tickets)

trips_[pair.first].push_back(pair.second);

for(auto& pair : trips_) {

auto& dests = pair.second;

std::sort(dests.begin(), dests.end());

}

const string kStart = "JFK";

visit(kStart);

return vector<string>(route_.crbegin(), route_.crend());

}

private:

// src -> {dst1, dest2, ..., destn}

unordered_map<string, deque<string>> trips_;

// ans (reversed)

vector<string> route_;

void visit(const string& src) {

auto& dests = trips_[src];

while (!dests.empty()) {

// Get the smallest dest

const string dest = dests.front();

// Remove the ticket

dests.pop_front();

// Visit dest

visit(dest);

}

// Add current node to the route

route_.push_back(src);

}

};

花花酱 LeetCode 295. Find Median from Data Stream O(logn) + O(1)

By zxi on September 12, 2017

Problem:

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Examples:

[2,3,4] , the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

void addNum(int num) – Add a integer number from the data stream to the data structure.
double findMedian() – Return the median of all elements so far.

For example:

addNum(1)

addNum(2)

findMedian() = 1.5

addNum(3)

findMedian() = 2

Idea:

Min/Max heap
Balanced binary search tree

Time Complexity:

add(num): O(logn)

findMedian(): O(logn)

Solution1:

// Author: Huahua

// Running Time: 152 ms

class MedianFinder {

public:

/** initialize your data structure here. */

MedianFinder() {}

// l_.size() >= r_.size()

void addNum(int num) {

if (l_.empty() || num <= l_.top()) {

l_.push(num);

} else {

r_.push(num);

}

// Step 2: Balence left/right

if (l_.size() < r_.size()) {

l_.push(r_.top());

r_.pop();

} else if (l_.size() - r_.size() == 2) {

r_.push(l_.top());

l_.pop();

}

double findMedian() {

if (l_.size() > r_.size()) {

return static_cast<double>(l_.top());

} else {

return (static_cast<double>(l_.top()) + r_.top()) / 2;

}

private:

priority_queue<int, vector<int>, less<int>> l_; // max-heap

priority_queue<int, vector<int>, greater<int>> r_; // min-heap

};

Solution 2:

// Author: Huahua

// Running time: 172 ms

class MedianFinder {

public:

/** initialize your data structure here. */

MedianFinder(): l_(m_.cend()), r_(m_.cend()) {}

// O(logn)

void addNum(int num) {

if (m_.empty()) {

l_ = r_ = m_.insert(num);

return;

}

m_.insert(num);

const size_t n = m_.size();

if (n & 1) {

// odd number

if (num >= *r_) {

l_ = r_;

} else {

// num < *r_, l_ could be invalidated

l_ = --r_;

}

} else {

if (num >= *r_)

++r_;

else

--l_;

}

// O(1)

double findMedian() {

return (static_cast<double>(*l_) + *r_) / 2;

}

private:

multiset<int> m_;

multiset<int>::const_iterator l_; // current left median

multiset<int>::const_iterator r_; // current right median

};

Related Problems

Huahua's Tech Road

花花酱 LeetCode 675. Cut Off Trees for Golf Event

花花酱 LeetCode 460. LFU Cache

花花酱 LeetCode 451. Sort Characters By Frequency

花花酱 LeetCode 332. Reconstruct Itinerary

花花酱 LeetCode 295. Find Median from Data Stream O(logn) + O(1)