Press "Enter" to skip to content

Huahua's Tech Road

花花酱 LeetCode 2218. Maximum Value of K Coins From Piles

By zxi on March 28, 2022

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Example 1:

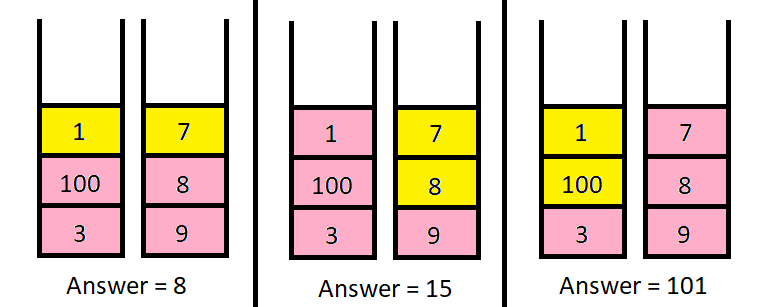
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

  • n == piles.length
  • 1 <= n <= 1000
  • 1 <= piles[i][j] <= 105
  • 1 <= k <= sum(piles[i].length) <= 2000

Solution: DP

let dp(i, k) be the maximum value of picking k elements using piles[i:n].

dp(i, k) = max(dp(i + 1, k), sum(piles[i][0~j]) + dp(i + 1, k – j – 1)), 0 <= j < len(piles[i])

Time complexity: O(n * m), m = sum(piles[i]) <= 2000
Space complexity: O(n * k)

Python

花花酱 LeetCode 2217. Find Palindrome With Fixed Length

By zxi on March 28, 2022

Given an integer array queries and a positive integer intLength, return an array answer where answer[i] is either the queries[i]th smallest positive palindrome of length intLength or -1 if no such palindrome exists.

A palindrome is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.

Example 1:

Input: queries = [1,2,3,4,5,90], intLength = 3
Output: [101,111,121,131,141,999]
Explanation:
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.

Example 2:

Input: queries = [2,4,6], intLength = 4
Output: [1111,1331,1551]
Explanation:
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.

Constraints:

  • 1 <= queries.length <= 5 * 104
  • 1 <= queries[i] <= 109
  • 1 <= intLength <= 15

Solution: Math

For even length e.g. 4, we work with length / 2, e.g. 2. Numbers: 10, 11, 12, …, 99, starting from 10, ends with 99, which consist of 99 – 10 + 1 = 90 numbers. For the x-th number, e.g. 88, the left part is 10 + 88 – 1 = 97, just mirror it o get the palindrome. 97|79. Thus we can answer a query in O(k/2) time which is critical.


For odd length e.g. 3 we work with length / 2 + 1, e.g. 2, Numbers: 10, 11, 12, 99. Drop the last digit and mirror the left part to get the palindrome. 101, 111, 121, …, 999.

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 2216. Minimum Deletions to Make Array Beautiful

By zxi on March 28, 2022

You are given a 0-indexed integer array nums. The array nums is beautiful if:

  • nums.length is even.
  • nums[i] != nums[i + 1] for all i % 2 == 0.

Note that an empty array is considered beautiful.

You can delete any number of elements from nums. When you delete an element, all the elements to the right of the deleted element will be shifted one unit to the left to fill the gap created and all the elements to the left of the deleted element will remain unchanged.

Return the minimum number of elements to delete from nums to make it beautiful.

Example 1:

Input: nums = [1,1,2,3,5]
Output: 1
Explanation: You can delete either nums[0] or nums[1] to make nums = [1,2,3,5] which is beautiful. It can be proven you need at least 1 deletion to make nums beautiful.

Example 2:

Input: nums = [1,1,2,2,3,3]
Output: 2
Explanation: You can delete nums[0] and nums[5] to make nums = [1,2,2,3] which is beautiful. It can be proven you need at least 2 deletions to make nums beautiful.

Constraints:

  • 1 <= nums.length <= 105
  • 0 <= nums[i] <= 105

Solution: Greedy + Two Pointers

If two consecutive numbers are the same, we must remove one. We don’t need to actually remove elements from array, just need to track how many elements have been removed so far.

i is the position in the original array, ans is the number of elements been removed. i – ans is the position in the updated array.

ans += nums[i – ans] == nums[i – ans + 1]

Remove the last element (just increase answer by 1) if the length of the new array is odd.

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 2215. Find the Difference of Two Arrays

By zxi on March 28, 2022

Given two 0-indexed integer arrays nums1 and nums2, return a list answer of size 2 where:

  • answer[0] is a list of all distinct integers in nums1 which are not present in nums2.
  • answer[1] is a list of all distinct integers in nums2 which are not present in nums1.

Note that the integers in the lists may be returned in any order.

Example 1:

Input: nums1 = [1,2,3], nums2 = [2,4,6]
Output: [[1,3],[4,6]]
Explanation:
For nums1, nums1[1] = 2 is present at index 0 of nums2, whereas nums1[0] = 1 and nums1[2] = 3 are not present in nums2. Therefore, answer[0] = [1,3].
For nums2, nums2[0] = 2 is present at index 1 of nums1, whereas nums2[1] = 4 and nums2[2] = 6 are not present in nums2. Therefore, answer[1] = [4,6].

Example 2:

Input: nums1 = [1,2,3,3], nums2 = [1,1,2,2]
Output: [[3],[]]
Explanation:
For nums1, nums1[2] and nums1[3] are not present in nums2. Since nums1[2] == nums1[3], their value is only included once and answer[0] = [3].
Every integer in nums2 is present in nums1. Therefore, answer[1] = [].

Constraints:

  • 1 <= nums1.length, nums2.length <= 1000
  • -1000 <= nums1[i], nums2[i] <= 1000

Solution: Hashtable

Use two hashtables to store the unique numbers of array1 and array2 respectfully.

Time complexity: O(m+n)
Space complexity: O(m+n)

C++

花花酱 LeetCode 2208. Minimum Operations to Halve Array Sum

By zxi on March 21, 2022

You are given an array nums of positive integers. In one operation, you can choose any number from nums and reduce it to exactly half the number. (Note that you may choose this reduced number in future operations.)

Return the minimum number of operations to reduce the sum of nums by at least half.

Example 1:

Input: nums = [5,19,8,1]
Output: 3
Explanation: The initial sum of nums is equal to 5 + 19 + 8 + 1 = 33.
The following is one of the ways to reduce the sum by at least half:
Pick the number 19 and reduce it to 9.5.
Pick the number 9.5 and reduce it to 4.75.
Pick the number 8 and reduce it to 4.
The final array is [5, 4.75, 4, 1] with a total sum of 5 + 4.75 + 4 + 1 = 14.75. 
The sum of nums has been reduced by 33 - 14.75 = 18.25, which is at least half of the initial sum, 18.25 >= 33/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.

Example 2:

Input: nums = [3,8,20]
Output: 3
Explanation: The initial sum of nums is equal to 3 + 8 + 20 = 31.
The following is one of the ways to reduce the sum by at least half:
Pick the number 20 and reduce it to 10.
Pick the number 10 and reduce it to 5.
Pick the number 3 and reduce it to 1.5.
The final array is [1.5, 8, 5] with a total sum of 1.5 + 8 + 5 = 14.5. 
The sum of nums has been reduced by 31 - 14.5 = 16.5, which is at least half of the initial sum, 16.5 >= 31/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.

Constraints:

  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 107

Solution: Greedy + PriorityQueue/Max Heap

Always half the largest number, put all the numbers onto a max heap (priority queue), extract the largest one, and put reduced number back.

Time complexity: O(nlogn)
Space complexity: O(n)

C++