花花酱 LeetCode 2218. Maximum Value of K Coins From Piles

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Example 1:

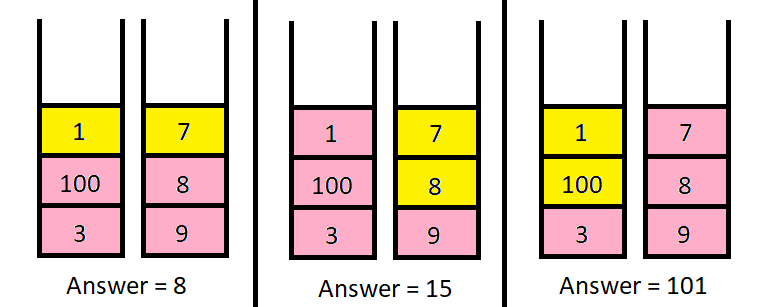
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

• n == piles.length
• 1 <= n <= 1000
• 1 <= piles[i][j] <= 105
• 1 <= k <= sum(piles[i].length) <= 2000

Solution: DP

let dp(i, k) be the maximum value of picking k elements using piles[i:n].

dp(i, k) = max(dp(i + 1, k), sum(piles[i][0~j]) + dp(i + 1, k – j – 1)), 0 <= j < len(piles[i])

Time complexity: O(n * m), m = sum(piles[i]) <= 2000
Space complexity: O(n * k)