花花酱 LeetCode 1477. Find Two Non-overlapping Sub-arrays Each With Target Sum

Given an array of integers arr and an integer target.

You have to find two non-overlapping sub-arrays of arr each with sum equal target. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is minimum.

Return the minimum sum of the lengths of the two required sub-arrays, or return -1 if you cannot find such two sub-arrays.

Example 1:

Input: arr = [3,2,2,4,3], target = 3
Output: 2
Explanation: Only two sub-arrays have sum = 3 ([3] and [3]). The sum of their lengths is 2.

Example 2:

Input: arr = [7,3,4,7], target = 7
Output: 2
Explanation: Although we have three non-overlapping sub-arrays of sum = 7 ([7], [3,4] and [7]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.

Example 3:

Input: arr = [4,3,2,6,2,3,4], target = 6
Output: -1
Explanation: We have only one sub-array of sum = 6.

Example 4:

Input: arr = [5,5,4,4,5], target = 3
Output: -1
Explanation: We cannot find a sub-array of sum = 3.

Example 5:

Input: arr = [3,1,1,1,5,1,2,1], target = 3
Output: 3
Explanation: Note that sub-arrays [1,2] and [2,1] cannot be an answer because they overlap.

Constraints:

• 1 <= arr.length <= 10^5
• 1 <= arr[i] <= 1000
• 1 <= target <= 10^8

Solution: Sliding Window + Best so far

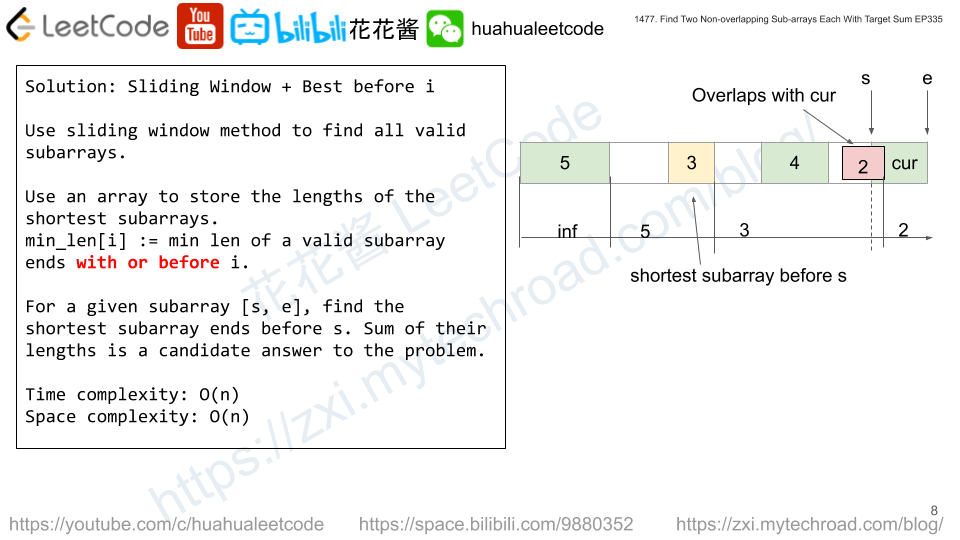
1. Use a sliding window to maintain a subarray whose sum is <= target
2. When the sum of the sliding window equals to target, we found a subarray [s, e]
3. Update ans with it’s length + shortest subarray which ends before s.
4. We can use an array to store the shortest subarray which ends before s.

Time complexity: O(n)
Space complexity: O(n)