You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route’s effort is the maximum absolute differencein heights between two consecutive cells of the route.
Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Example 1:
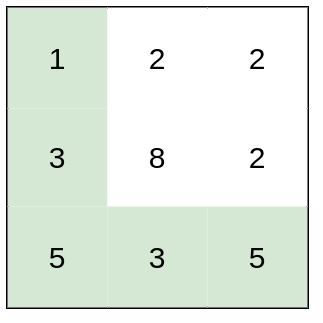
Input: heights = [[1,2,2],[3,8,2],[5,3,5]] Output: 2 Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells. This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
Example 2:
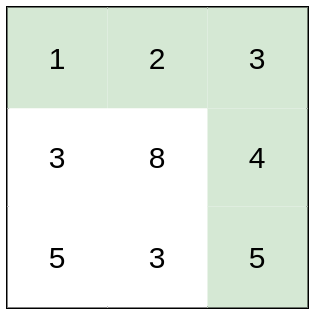
Input: heights = [[1,2,3],[3,8,4],[5,3,5]] Output: 1 Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
Example 3:
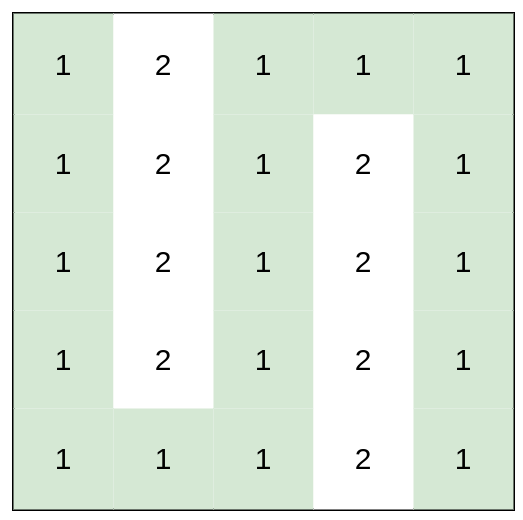
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]] Output: 0 Explanation: This route does not require any effort.
Constraints:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 106
Solution: “Lazy BFS / DP”
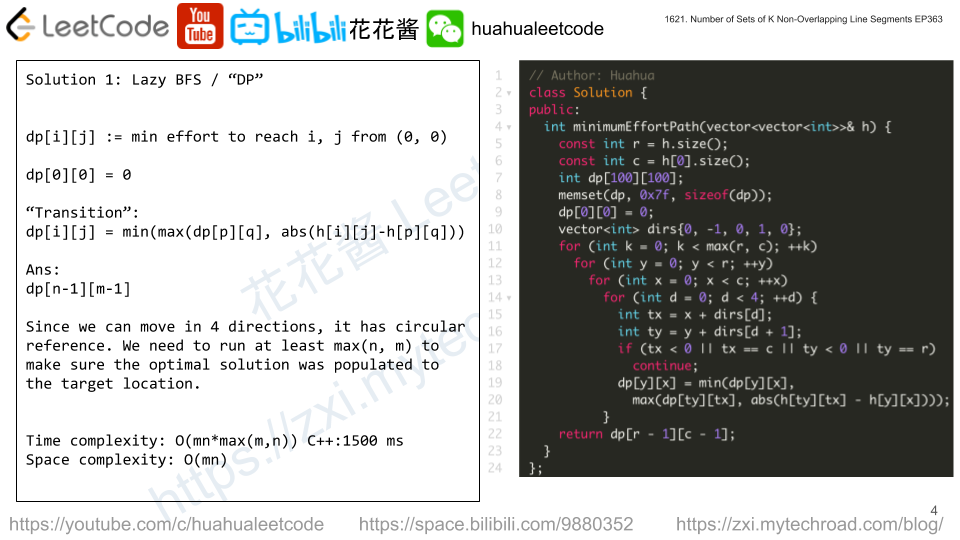
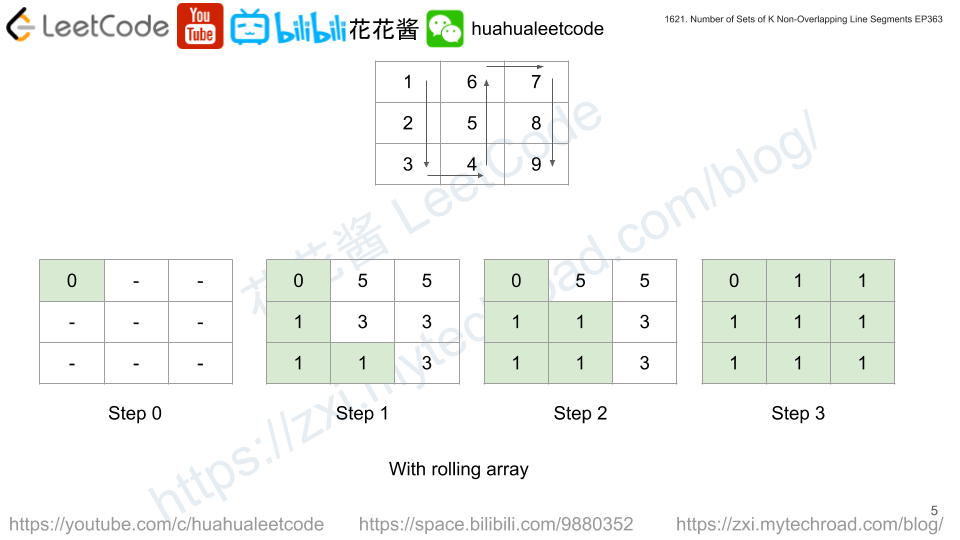
dp[y][x] = min(max(dp[ty][tx], abs(h[ty][tx] – h[y][x]))) (x, y) and (tx, ty) are neighbors
repeat this process for at most rows * cols times.
if dp does not change after one round which means we found the optimal solution and can break earlier.
Time complexity: O(n^2*m^2))
Space complexity: O(nm)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// Author: Huahua, 824 ms class Solution { public: int minimumEffortPath(vector<vector<int>>& heights) { const int r = heights.size(); const int c = heights[0].size(); int dp[100][100]; memset(dp, 0x7f, sizeof(dp)); dp[0][0] = 0; vector<int> dirs{0, -1, 0, 1, 0}; for (int k = 0; k < r * c; ++k) { bool stable = true; for (int y = 0; y < r; ++y) for (int x = 0; x < c; ++x) for (int d = 0; d < 4; ++d) { int tx = x + dirs[d]; int ty = y + dirs[d + 1]; if (tx < 0 || tx == c || ty < 0 || ty == r) continue; int t = max(dp[ty][tx], abs(heights[ty][tx] - heights[y][x])); if (t < dp[y][x]) { stable = false; dp[y][x] = t; } } if (stable) break; } return dp[r - 1][c - 1]; } }; |
Solution 2: Binary Search + BFS
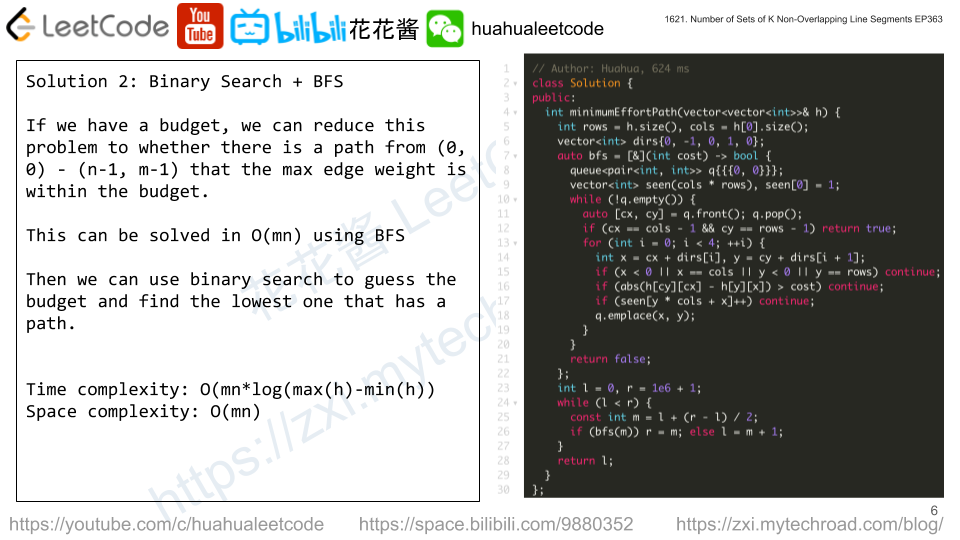
Use binary search to guess a cost and then check whether there is path that is under the cost.
Time complexity: O(mn*log(max(h) – min(h)))
Space complexity: O(mn)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
// Author: Huahua, 620 ms class Solution { public: int minimumEffortPath(vector<vector<int>>& heights) { const int rows = heights.size(); const int cols = heights[0].size(); vector<int> dirs{0, -1, 0, 1, 0}; auto bfs = [&](int cost) -> bool { queue<pair<int, int>> q; vector<int> seen(cols * rows); q.emplace(0, 0); seen[0] = 1; while (!q.empty()) { auto [cx, cy] = q.front(); q.pop(); if (cx == cols - 1 && cy == rows - 1) return true; for (int i = 0; i < 4; ++i) { int x = cx + dirs[i]; int y = cy + dirs[i + 1]; if (x < 0 || x == cols || y < 0 || y == rows) continue; if (abs(heights[cy][cx] - heights[y][x]) > cost) continue; if (seen[y * cols + x]++) continue; q.emplace(x, y); } } return false; }; int l = 0, r = 1e6 + 1; while (l < r) { const int m = l + (r - l) / 2; if (bfs(m)) { r = m; } else { l = m + 1; } } return l; } }; |
Solution 3: Dijkstra

Time complexity: O(mnlog(mn))
Space complexity: O(mn)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
// Author: Huahua, 216 ms class Solution { public: int minimumEffortPath(vector<vector<int>>& heights) { const vector<int> dirs{0, -1, 0, 1, 0}; const int rows = heights.size(); const int cols = heights[0].size(); using Node = pair<int, int>; priority_queue<Node, vector<Node>, greater<Node>> q; vector<int> dist(rows * cols, INT_MAX / 2); q.emplace(0, 0); dist[0] = 0; while (!q.empty()) { auto [t, u] = q.top(); q.pop(); if (u == rows * cols - 1) return t; if (t > dist[u]) continue; const int ux = u % cols; const int uy = u / cols; for (int i = 0; i < 4; ++i) { const int x = ux + dirs[i]; const int y = uy + dirs[i + 1]; if (x < 0 || x == cols || y < 0 || y == rows) continue; const int v = y * cols + x; const int c = abs(heights[uy][ux] - heights[y][x]); if (max(t, c) >= dist[v]) continue; q.emplace(dist[v] = max(t, c), v); } } return -1; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment