There are n cities numbered from 0 to n-1 and n-1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by connections where connections[i] = [a, b] represents a road from city a to b.
This year, there will be a big event in the capital (city 0), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.
It’s guaranteed that each city can reach the city 0 after reorder.
Example 1:
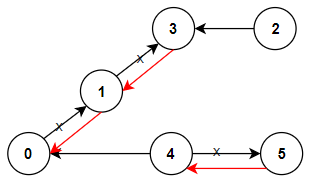
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]] Output: 3 Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]] Output: 2 Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 3:
Input: n = 3, connections = [[1,0],[2,0]] Output: 0
Constraints:
2 <= n <= 5 * 10^4connections.length == n-1connections[i].length == 20 <= connections[i][0], connections[i][1] <= n-1connections[i][0] != connections[i][1]
Solution: BFS
Augment the graph
g[u][v] = 1, g[v][u] = 0, u->v is an edge in the original graph.
BFS from 0, sum up all the edge costs to visit all the nodes.
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
// Author: Huahua class Solution { public: int minReorder(int n, vector<vector<int>>& connections) { vector<vector<pair<int, int>>> g(n); // u -> {v, cost} for (const auto& e : connections) { g[e[0]].emplace_back(e[1], 1); // u -> v, needs flip g[e[1]].emplace_back(e[0], 0); // v -> u, no cost } int ans = 0; queue<int> q{{0}}; vector<int> seen(n); while (!q.empty()) { int cur = q.front(); q.pop(); seen[cur] = 1; for (const auto& [nxt, cost] : g[cur]) { if (seen[nxt]) continue; ans += cost; q.push(nxt); } } return ans; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment