Posts tagged as “dp”

花花酱 LeetCode 940. Distinct Subsequences II

By zxi on November 14, 2018

Problem

Given a string S, count the number of distinct, non-empty subsequences of S .

Since the result may be large, return the answer modulo 10^9 + 7.

Example 1:

Input: "abc"
Output: 7
Explanation: The 7 distinct subsequences are "a", "b", "c", "ab", "ac", "bc", and "abc".

Example 2:

Input: "aba"
Output: 6
Explanation: The 6 distinct subsequences are "a", "b", "ab", "ba", "aa" and "aba".

Example 3:

Input: "aaa"
Output: 3
Explanation: The 3 distinct subsequences are "a", "aa" and "aaa".

Note:

S contains only lowercase letters.
1 <= S.length <= 2000

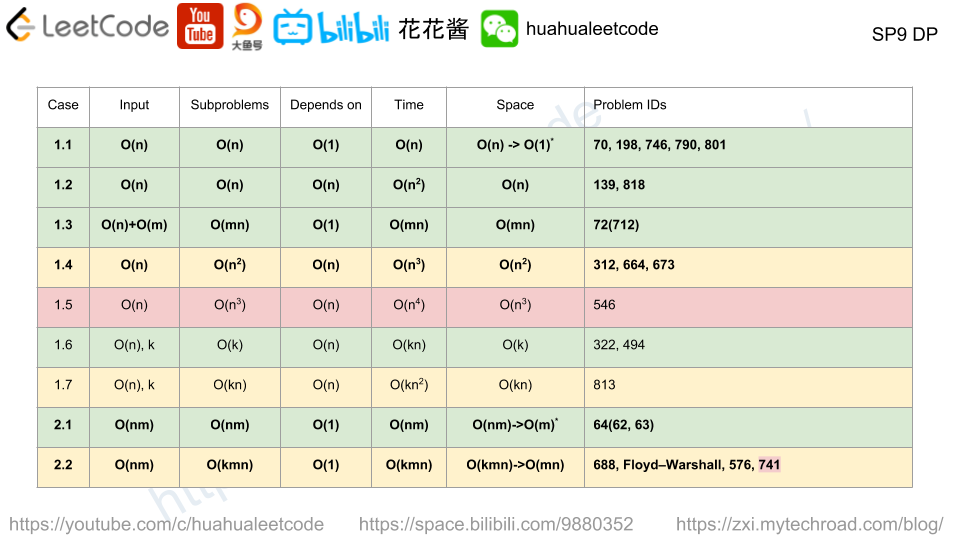
Solution: DP

counts[i][j] := # of distinct sub sequences of s[1->i] and ends with letter j. (‘a'<= j <= ‘z’)

Initialization:

counts[*][*] = 0

Transition:

counts[i][j] = sum(counts[i-1]) + 1 if s[i] == j else counts[i-1][j]

ans = sum(counts[n])

e.g. S = “abc”

counts[1] = {‘a’ : 1}
counts[2] = {‘a’ : 1, ‘b’ : 1 + 1 = 2}
counts[3] = {‘a’ : 1, ‘b’ : 2, ‘c’: 1 + 2 + 1 = 4}
ans = sum(counts[3]) = 1 + 2 + 4 = 7

Time complexity: O(N*26)

Space complexity: O(N*26) -> O(26)

C++

// Author: Huahua, running time: 12 ms

class Solution {

public:

int distinctSubseqII(string S) {

constexpr int kMod = 1e9 + 7;

std::vector<int> counts(26);

for (char c : S)

counts[c - 'a'] = accumulate(begin(counts), end(counts), 1L) % kMod;

return accumulate(begin(counts), end(counts), 0L) % kMod;

}

};

Python3

# Author: Huahua, running time: 64 ms

class Solution:

def distinctSubseqII(self, S):

kMod = 10**9 + 7

dp = {}

for c in S:

dp[c] = (sum(dp.values()) + 1) % kMod

return sum(dp.values()) % kMod

Knapsack Problem 背包问题

By zxi on November 10, 2018

Videos

上期节目中我们对动态规划做了一个总结，这期节目我们来聊聊背包问题。

背包问题是一个NP-complete的组合优化问题，Search的方法需要O(2^N)时间才能获得最优解。而使用动态规划，我们可以在伪多项式（pseudo-polynomial time）时间内获得最优解。

0-1 Knapsack Problem 0-1背包问题

Problem

Given N items, w[i] is the weight of the i-th item and v[i] is value of the i-th item. Given a knapsack with capacity W. Maximize the total value. Each item can be use 0 or 1 time.

0-1背包问题的通常定义是：一共有N件物品，第i件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够获得的最大价值是多少？每件物品可以使用0次或者1次。

例子：

重量 w = [1, 1, 2, 2]

价值 v = [1, 3, 4, 5]

背包承重 W = 4

最大价值为9，可以选第1,2,4件物品，也可以选第3，4件物品；总重量为4，总价值为9。

动态规划的状态转移方程为：

1	dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]] + v[i])

Solutions

Search

def knapsack01DFS(w, v, W):

def dfs(s, cur_w, cur_v, ans):

ans[0] = max(ans[0], cur_v)

if s == N: return

for i in range(s, N):

if cur_w + w[i] <= W:

dfs(i + 1, cur_w + w[i], cur_v + v[i], ans)

ans = [0]

dfs(0, 0, 0, ans)

return ans[0]

DP2

def knapsack01(w, v, W):

dp = [[0] * (W + 1) for _ in range(N+1)]

for i in range(1, N + 1):

dp[i] = dp[i-1].clone()

for j in range(w[i], W + 1):

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1])

return max(dp[N])

DP1/tmp

def knapsack01R(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

tmp = list(dp)

for j in range(w[i], W + 1):

tmp[j] = max(tmp[j], dp[j - w[i]] + v[i])

dp = tmp

return max(dp)

DP1/push

def knapsack01R2(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

for j in range(W, w[i] - 1, -1):

dp[j] = max(dp[j], dp[j - w[i]] + v[i])

return max(dp)

DP1/pull

def knapsack01R1(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

for j in range(W - w[i], -1, -1):

dp[j + w[i]] = max(dp[j + w[i]], dp[j] + v[i])

return max(dp)

Unbounded Knapsack Problem 完全背包

完全背包、多重背包是常见的变形。和01背包的区别在于，完全背包每件物品可以使用无限多次，而多重背包每件物品最多可以使用n[i]次。两个问题都可以转换成01背包问题进行求解。

但是Naive的转换会大大增加时间复杂度：

完全背包：“复制”第i件物品到一共有 W/w[i] 件

多重背包：“复制”第i件物品到一共有 n[i] 件

然后直接调用01背包进行求解。

时间复杂度：

完全背包 O(Σ(W/w[i])*W)

多重背包 O(Σn[i]*W)

不难看出时间复杂度 = O(物品数量*背包承重)

背包承重是给定的，要降低运行时候，只有减少物品数量。但怎样才能减少总的物品数量呢？

这就涉及到二进制思想：任何一个正整数都可以用 (1, 2, 4, …, 2^K)的组合来表示。例如14 = 2 + 4 + 8。
原本需要放入14件相同的物品，现在只需要放入3件（重量和价值是原物品的2倍，4倍，8倍）。大幅降低了总的物品数量从而降低运行时间。

完全背包：对于第i件物品，我们只需要创建k = log(W/w[i])件虚拟物品即可。

每件虚拟物品的重量和价值为：1*(w[i], v[i]), 2*(w[i], v[i]), …, 2^k*(w[i], v[i])。

多重背包：对于第i件物品，我们只需要创建k + 1件虚拟物品即可，其中k = log(n[i])。

每件虚拟物品的重量和价值为：1*(w[i], v[i]), 2*(w[i], v[i]), …, 2^(k-1)*(w[i], v[i]), 以及 (n[i] – 2^k – 1) * (w[i], v[i])。

例如：n[i] = 14, k = 3, 虚拟物品的倍数为 1, 2, 4 和 7，这4个数组合可以组成1 ~ 14中的任何一个数，并且不会>14，即不超过n[i]。

二进制转换后直接调用01背包即可

时间复杂度：

完全背包 O(Σlog(W/w[i])*W)

多重背包 O(Σlog(n[i])*W)

空间复杂度 O(W)

其实完全背包和多重背包都可以在 O(NW)时间内完成，前者在视频中有讲到，后者属于超纲内容，以后有机会再和大家深入分享。

Bounded Knapsack Problem 多重背包

花花酱 LeetCode 935. Knight Dialer

By zxi on November 4, 2018

Problem

https://leetcode.com/problems/knight-dialer/description/

A chess knight can move as indicated in the chess diagram below:

This time, we place our chess knight on any numbered key of a phone pad (indicated above), and the knight makes N-1 hops. Each hop must be from one key to another numbered key.

Each time it lands on a key (including the initial placement of the knight), it presses the number of that key, pressing N digits total.

How many distinct numbers can you dial in this manner?

Since the answer may be large, output the answer modulo 10^9 + 7.

Example 1:

Input: 1
Output: 10

Example 2:

Input: 2
Output: 20

Example 3:

Input: 3
Output: 46

Note:

1 <= N <= 5000

Solution: DP

V1

We can define dp[k][i][j] as # of ways to dial and the last key is (j, i) after k steps

Note: dp[*][3][0], dp[*][3][2] are always zero for all the steps.

Init: dp[0][i][j] = 1

Transition: dp[k][i][j] = sum(dp[k – 1][i + dy][j + dx]) 8 ways of move from last step.

ans = sum(dp[k])

Time complexity: O(kmn) or O(k * 12 * 8) = O(k)

Space complexity: O(kmn) -> O(mn) or O(12*8) = O(1)

V2

define dp[k][i] as # of ways to dial and the last key is i after k steps

init: dp[0][0:10] = 1

transition: dp[k][i] = sum(dp[k-1][j]) that j can move to i

ans: sum(dp[k])

Time complexity: O(k * 10) = O(k)

Space complexity: O(k * 10) -> O(10) = O(1)

C++ V1

// Author: Huahua, 96 ms

class Solution {

public:

int knightDialer(int N) {

constexpr int kMod = 1e9 + 7;

int dirs[8][2] = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};

vector<vector<int>> dp(4, vector<int>(3, 1));

dp[3][0] = dp[3][2] = 0;

for (int k = 1; k < N; ++k) {

vector<vector<int>> tmp(4, vector<int>(3));

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 3; ++j) {

if (i == 3 && j != 1) continue;

for (int d = 0; d < 8; ++d) {

int tx = j + dirs[d][0];

int ty = i + dirs[d][1];

if (tx < 0 || ty < 0 || tx >= 3 || ty >= 4) continue;

tmp[i][j] = (tmp[i][j] + dp[ty][tx]) % kMod;

}

dp.swap(tmp);

}

int ans = 0;

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 3; ++j)

ans = (ans + dp[i][j]) % kMod;

return ans;

}

};

C++ V2

// Author: Huahua, 24 ms

public:

int knightDialer(int N) {

constexpr int kMod = 1e9 + 7;

vector<vector<int>> moves{{4,6},{8,6},{7,9},{4,8},{3,9,0},{},{1,7,0},{2,6},{1,3},{2,4}};

vector<int> dp(10, 1);

for (int k = 1; k < N; ++k) {

vector<int> tmp(10);

for (int i = 0; i < 10; ++i)

for (int nxt : moves[i])

tmp[nxt] = (tmp[nxt] + dp[i]) % kMod;

dp.swap(tmp);

}

int ans = 0;

for (int i = 0; i < 10; ++i)

ans = (ans + dp[i]) % kMod;

return ans;

}

};

Problem

Given a square array of integers A, we want the minimum sum of a falling path through A.

A falling path starts at any element in the first row, and chooses one element from each row. The next row’s choice must be in a column that is different from the previous row’s column by at most one.

Example 1:

Input: [[1,2,3],[4,5,6],[7,8,9]]
Output: 12
Explanation: 
The possible falling paths are:

[1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9]
[2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9]
[3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]

The falling path with the smallest sum is [1,4,7], so the answer is 12.

Note:

1 <= A.length == A[0].length <= 100
-100 <= A[i][j] <= 100

Solution: DP

Time complexity: O(mn)

Space complexity: O(mn)

C++

// Author: Huahua, 12 ms

class Solution {

public:

int minFallingPathSum(vector<vector<int>>& A) {

int n = A.size();

int m = A[0].size();

vector<vector<int>> dp(n + 2, vector<int>(m + 2));

for (int i = 1; i <= n; ++i) {

dp[i][0] = dp[i][m + 1] = INT_MAX;

for (int j = 1; j <= m; ++j)

dp[i][j] = *min_element(dp[i - 1].begin() + j - 1,

dp[i - 1].begin() + j + 2) + A[i - 1][j - 1];

}

return *min_element(dp[n].begin() + 1, dp[n].end() - 1);

}

};

C++/in place

// Author: Huahua, 12 ms

class Solution {

public:

int minFallingPathSum(vector<vector<int>>& A) {

int n = A.size();

int m = A[0].size();

for (int i = 1; i < n; ++i)

for (int j = 0; j < m; ++j) {

int sum = A[i - 1][j];

if (j > 0) sum = min(sum, A[i - 1][j - 1]);

if (j < m - 1) sum = min(sum, A[i - 1][j + 1]);

A[i][j] += sum;

}

return *min_element(begin(A.back()), end(A.back()));

}

};

Posts tagged as “dp”

花花酱 LeetCode 940. Distinct Subsequences II

Problem

Solution: DP

C++

Python3

Knapsack Problem 背包问题

Videos

0-1 Knapsack Problem 0-1背包问题

Problem

Solutions

Search

DP2

DP1/tmp

DP1/push

DP1/pull

Unbounded Knapsack Problem 完全背包

Bounded Knapsack Problem 多重背包

花花酱 LeetCode 935. Knight Dialer

Problem

Solution: DP

V1

V2

C++ V1

C++ V2

Related Problem

花花酱 LeetCode DP Summary 动态规划总结

Category 1.1

Template

花花酱 LeetCode 931. Minimum Falling Path Sum

Problem

Solution: DP

C++

C++/in place