花花酱 LeetCode 975. Odd Even Jump

You are given an integer array A.  From some starting index, you can make a series of jumps.  The (1st, 3rd, 5th, …) jumps in the series are called odd numbered jumps, and the (2nd, 4th, 6th, …) jumps in the series are called even numbered jumps.

You may from index i jump forward to index j (with i < j) in the following way:

• During odd numbered jumps (ie. jumps 1, 3, 5, …), you jump to the index j such that A[i] <= A[j] and A[j] is the smallest possible value.  If there are multiple such indexes j, you can only jump to the smallest such index j.
• During even numbered jumps (ie. jumps 2, 4, 6, …), you jump to the index j such that A[i] >= A[j] and A[j] is the largest possible value.  If there are multiple such indexes j, you can only jump to the smallest such index j.
• (It may be the case that for some index i, there are no legal jumps.)

A starting index is good if, starting from that index, you can reach the end of the array (index A.length - 1) by jumping some number of times (possibly 0 or more than once.)

Return the number of good starting indexes.

Example 1:

Input: [10,13,12,14,15] 
Output: 2 

Example 2:

Input: [2,3,1,1,4] 
Output: 3 

Example 3:

Input: [5,1,3,4,2] 
Output: 3

Note:

1. 1 <= A.length <= 20000
2. 0 <= A[i] < 100000

Solution: Binary Search + DP

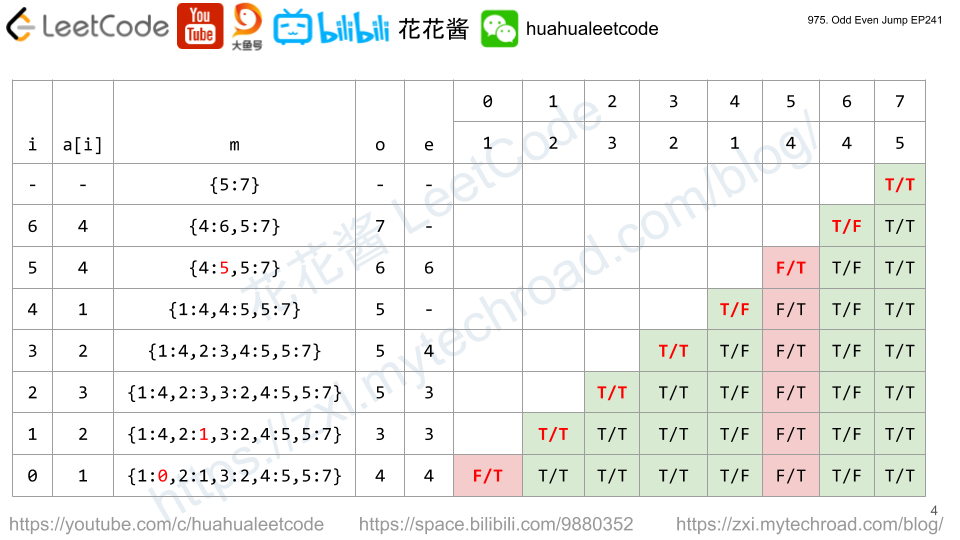
Time complexity: O(nlogn)
Space complexity: O(n)