Posts tagged as “dp”

花花酱 LeetCode 818. Race Car

By zxi on April 15, 2018

Problem

题目大意：初始位置0速度+1，每次你可以加速（速度*2）或者倒车（速度变成-1*dir）。问最少需要执行多少步操作能够到达T。

https://leetcode.com/problems/race-car/description/

Your car starts at position 0 and speed +1 on an infinite number line. (Your car can go into negative positions.)

Your car drives automatically according to a sequence of instructions A (accelerate) and R (reverse).

When you get an instruction “A”, your car does the following: position += speed, speed *= 2.

When you get an instruction “R”, your car does the following: if your speed is positive then speed = -1 , otherwise speed = 1. (Your position stays the same.)

For example, after commands “AAR”, your car goes to positions 0->1->3->3, and your speed goes to 1->2->4->-1.

Now for some target position, say the length of the shortest sequence of instructions to get there.

Example 1:
Input: 
target = 3
Output: 2
Explanation: 
The shortest instruction sequence is "AA".
Your position goes from 0->1->3.

Example 2:
Input: 
target = 6
Output: 5
Explanation: 
The shortest instruction sequence is "AAARA".
Your position goes from 0->1->3->7->7->6.

Note:

1 <= target <= 10000.

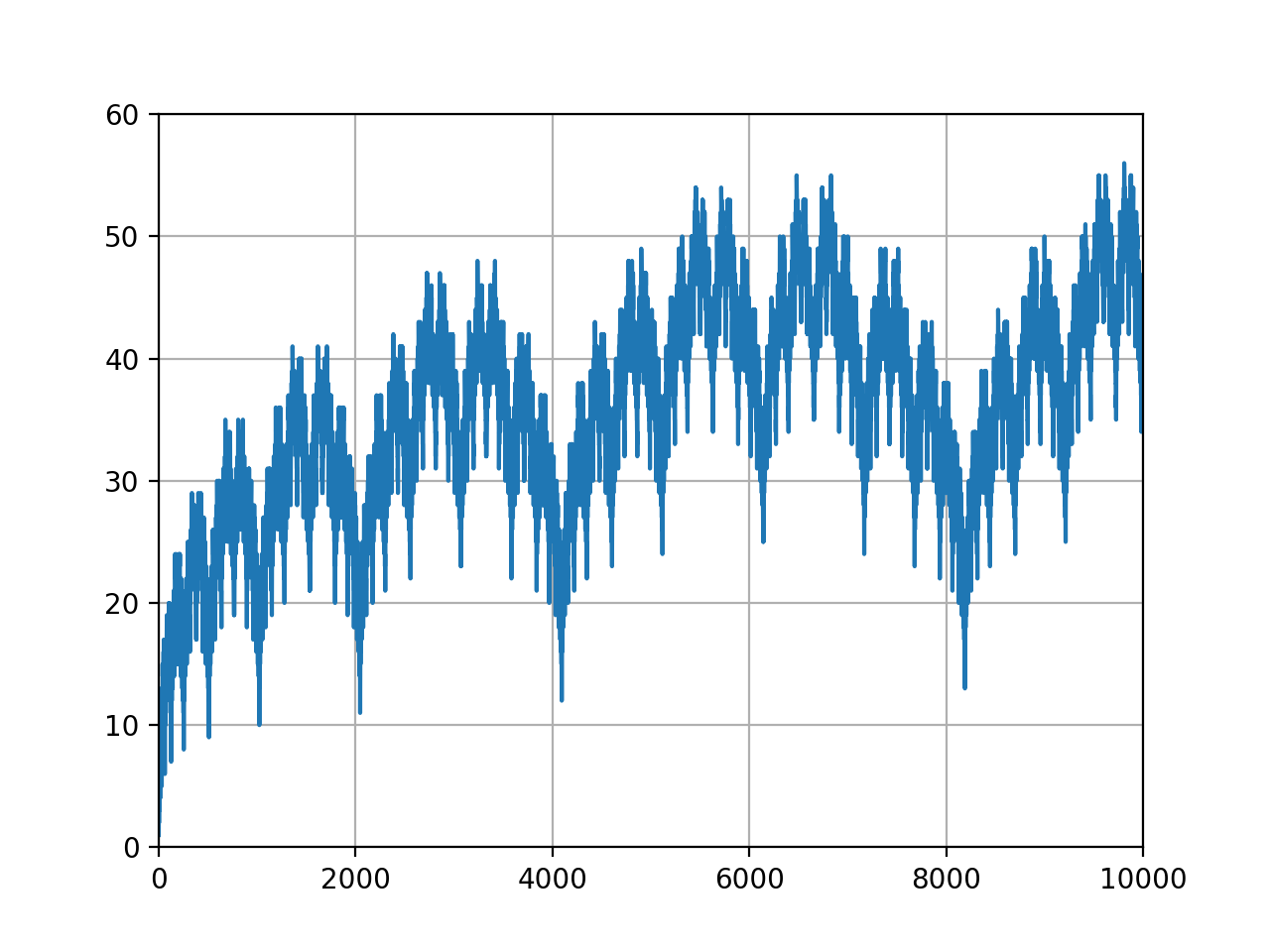
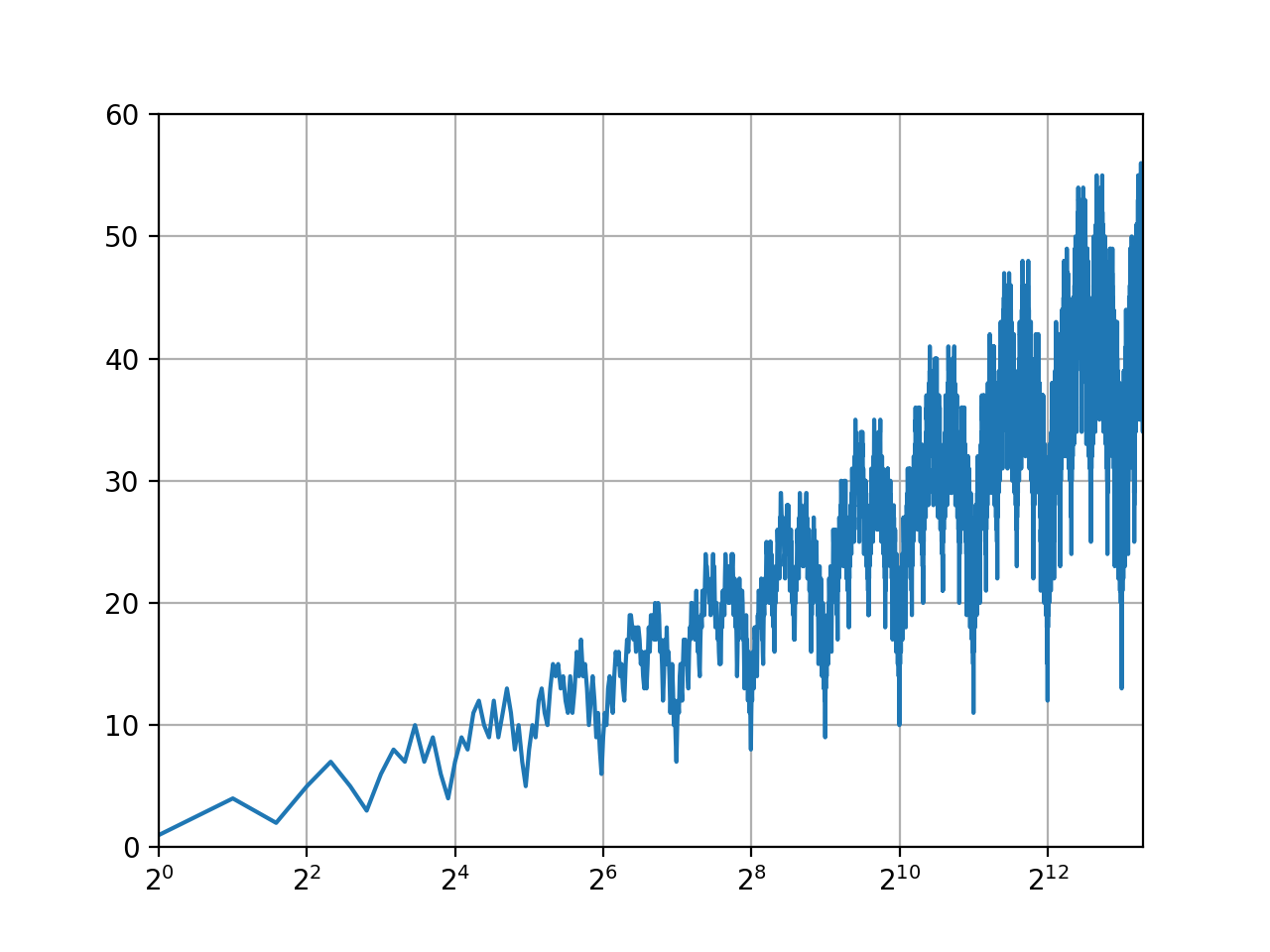
Visualization of the Solution

Solution 1: BFS

C++/Str

// Author: Huahua

// Running time: 221 ms

class Solution {

public:

int racecar(int target) {

queue<pair<int, int>> q;

q.push({0, 1});

unordered_set<string> v;

v.insert("0_1");

v.insert("0_-1");

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

auto p = q.front(); q.pop();

int pos = p.first;

int speed = p.second;

{

int pos1 = pos + speed;

int speed1 = speed * 2;

pair<int, int> p1{pos1, speed1};

if (pos1 == target) return steps + 1;

if (p1.first > 0 && p1.first < 2 * target)

q.push(p1);

}

{

int speed2 = speed > 0 ? -1 : 1;

pair<int, int> p2{pos, speed2};

string key2 = to_string(pos) + "_" + to_string(speed2);

if (!v.count(key2)) {

q.push(p2);

v.insert(key2);

}

++steps;

}

return -1;

}

};

C++/Int

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

int racecar(int target) {

queue<pair<int, int>> q;

q.push({0, 1});

unordered_set<int> v;

v.insert({0, 2});

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

auto p = q.front(); q.pop();

int pos = p.first;

int speed = p.second;

pair<int, int> p1 = {pos + speed, speed * 2};

if (p1.first == target) return steps + 1;

if (p1.first > 0 && p1.first + speed < 2 * target)

q.push(p1);

int speed2 = speed > 0 ? -1 : 1;

pair<int, int> p2 = {pos, speed2};

int key = (pos << 2) | (speed2 + 1);

if (!v.count(key) && p2.first >= target / 2) {

q.push(p2);

v.insert(key);

}

++steps;

}

return -1;

}

};

Solution 2: DP O(TlogT)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int racecar(int target) {

m_ = vector<int>(target + 1, 0);

return dp(target);

}

private:

vector<int> m_;

int dp(int t) {

if (m_[t] > 0) return m_[t];

int n = ceil(log2(t + 1));

// AA...A (nA) best case

if (1 << n == t + 1) return m_[t] = n;

// AA...AR (nA + 1R) + dp(left)

m_[t] = n + 1 + dp((1 << n) - 1 - t);

for (int m = 0; m < n - 1; ++m) {

int cur = (1 << (n - 1)) - (1 << m);

//AA...ARA...AR (n-1A + 1R + mA + 1R) + dp(left)

m_[t] = min(m_[t], n + m + 1 + dp(t - cur));

}

return m_[t];

}

};

Solution 3: DP O(T^2)

m[t][d] : min steps to reach t and facing d (0 = right, 1 = left)

Time Complexity: O(n^2)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 469 ms

constexpr int kMaxT = 10000;

int m[kMaxT + 1][2]={0};

class Solution {

public:

int racecar(int target) {

if (m[1][0] == 0) {

for (int t = 1; t <= kMaxT; ++t) {

const int n = ceil(log2(t + 1));

if (1 << n == t + 1) {

m[t][0] = n;

m[t][1] = n + 1;

continue;

}

const int l = (1 << n) - 1 - t;

m[t][0] = n + 1 + min(m[l][1], m[l][0] + 1);

m[t][1] = n + 1 + min(m[l][0], m[l][1] + 1);

for (int i = 1; i < t; ++i) {

const int mi = min(m[i][0] + 2, m[i][1] + 1);

m[t][0] = min(m[t][0], m[t - i][0] + mi);

m[t][1] = min(m[t][1], m[t - i][1] + mi);

}

return min(m[target][0], m[target][1]);

}

};

C++/opt

// Author: Huahua

// Running time: 361 ms

typedef unsigned char uint8;

constexpr int kMaxT = 10000;

uint8 m[kMaxT + 1][2]={0};

inline uint8 MIN(uint8 a, uint8 b) {

return a < b ? a : b;

}

class Solution {

public:

int racecar(int target) {

if (m[1][0] == 0) {

for (int t = 1; t <= kMaxT; ++t) {

const int n = ceil(log2(t + 1));

if (1 << n == t + 1) {

m[t][0] = n;

m[t][1] = n + 1;

continue;

}

const int l = (1 << n) - 1 - t;

m[t][0] = n + 1 + MIN(m[l][1], (uint8)(m[l][0] + 1));

m[t][1] = n + 1 + MIN(m[l][0], (uint8)(m[l][1] + 1));

for (int i = 1; i < t; ++i) {

const int mi = MIN(m[i][0] + 2, m[i][1] + 1);

m[t][0] = MIN(m[t][0], (uint8)(m[t - i][0] + mi));

m[t][1] = MIN(m[t][1], (uint8)(m[t - i][1] + mi));

}

return min(m[target][0], m[target][1]);

}

};

Java

// Author: Huahua

// Running time: 562 ms

class Solution {

private static int[][] m;

public int racecar(int target) {

if (m == null) {

final int kMaxT = 10000;

m = new int[kMaxT + 1][2];

for (int t = 1; t <= kMaxT; ++t) {

int n = (int)Math.ceil(Math.log(t + 1) / Math.log(2));

if (1 << n == t + 1) {

m[t][0] = n;

m[t][1] = n + 1;

continue;

}

int l = (1 << n) - 1 - t;

m[t][0] = n + 1 + Math.min(m[l][1], m[l][0] + 1);

m[t][1] = n + 1 + Math.min(m[l][0], m[l][1] + 1);

for (int i = 1; i < t; ++i)

for (int d = 0; d <= 1; d++)

m[t][d] = Math.min(m[t][d], Math.min(

m[i][0] + 2 + m[t - i][d],

m[i][1] + 1 + m[t - i][d]));

}

return Math.min(m[target][0], m[target][1]);

}

花花酱 LeetCode 813. Largest Sum of Averages

By zxi on April 9, 2018

Problem

题目大意：把一个数组分成k个段，求每段平均值和的最大值。

https://leetcode.com/problems/largest-sum-of-averages/description/

We partition a row of numbers A into at most K adjacent (non-empty) groups, then our score is the sum of the average of each group. What is the largest score we can achieve?

Note that our partition must use every number in A, and that scores are not necessarily integers.

Example:
Input: 
A = [9,1,2,3,9]
K = 3
Output: 20
Explanation: 
The best choice is to partition A into [9], [1, 2, 3], [9]. The answer is 9 + (1 + 2 + 3) / 3 + 9 = 20.
We could have also partitioned A into [9, 1], [2], [3, 9], for example.
That partition would lead to a score of 5 + 2 + 6 = 13, which is worse.

Note:

1 <= A.length <= 100.
1 <= A[i] <= 10000.
1 <= K <= A.length.
Answers within 10^-6 of the correct answer will be accepted as correct.

Idea

DP, use dp[k][i] to denote the largest average sum of partitioning first i elements into k groups.

Init

dp[1][i] = sum(a[0] ~ a[i – 1]) / i, for i in 1, 2, … , n.

Transition

dp[k][i] = max(dp[k – 1][j] + sum(a[j] ~ a[i – 1]) / (i – j)) for j in k – 1,…,i-1.

that is find the best j such that maximize dp[k][i]

largest sum of partitioning first j elements (a[0] ~ a[j – 1]) into k – 1 groups (already computed)

+ average of a[j] ~ a[i – 1] (partition a[j] ~ a[i – 1] into 1 group).

Answer

dp[K][n]

Solution 1: DP

Time complexity: O(kn^2)

Space complexity: O(kn)

C++

// Author: Huahua

// Running time: 9 ms

class Solution {

public:

double largestSumOfAverages(vector<int>& A, int K) {

const int n = A.size();

vector<vector<double>> dp(K + 1, vector<double>(n + 1, 0.0));

vector<double> sums(n + 1, 0.0);

for (int i = 1; i <= n; ++i) {

sums[i] = sums[i - 1] + A[i - 1];

dp[1][i] = static_cast<double>(sums[i]) / i;

}

for (int k = 2; k <= K; ++k)

for (int i = k; i <= n; ++i)

for (int j = k - 1; j < i; ++j)

dp[k][i] = max(dp[k][i], dp[k - 1][j] + (sums[i] - sums[j]) / (i - j));

return dp[K][n];

}

};

C++ O(n) space

// Author: Huahua

// Running time: 8 ms

class Solution {

public:

double largestSumOfAverages(vector<int>& A, int K) {

const int n = A.size();

vector<double> dp(n + 1, 0.0);

vector<double> sums(n + 1, 0.0);

for (int i = 1; i <= n; ++i) {

sums[i] = sums[i - 1] + A[i - 1];

dp[i] = static_cast<double>(sums[i]) / i;

}

for (int k = 2; k <= K; ++k) {

vector<double> tmp(n + 1, 0.0);

for (int i = k; i <= n; ++i)

for (int j = k - 1; j < i; ++j)

tmp[i] = max(tmp[i], dp[j] + (sums[i] - sums[j]) / (i - j));

dp.swap(tmp);

}

return dp[n];

}

};

Solution 2: DFS + memoriation

C++

// Author: Huahua

// Running time: 10 ms

class Solution {

public:

double largestSumOfAverages(vector<int>& A, int K) {

const int n = A.size();

m_ = vector<vector<double>>(K + 1, vector<double>(n + 1, 0.0));

sums_ = vector<double>(n + 1, 0.0);

for (int i = 1; i <= n; ++i)

sums_[i] = sums_[i - 1] + A[i - 1];

return LSA(A, n, K);

}

private:

vector<vector<double>> m_;

vector<double> sums_;

// Largest sum of averages for first n elements in A paritioned into k groups

double LSA(const vector<int>& A, int n, int k) {

if (m_[k][n] > 0) return m_[k][n];

if (k == 1) return sums_[n] / n;

for (int i = k - 1; i < n; ++i)

m_[k][n] = max(m_[k][n], LSA(A, i, k - 1) + (sums_[n] - sums_[i]) / (n - i));

return m_[k][n];

}

};

花花酱 LeetCode 552. Student Attendance Record II

By zxi on March 22, 2018

Problem

Given a positive integer n, return the number of all possible attendance records with length n, which will be regarded as rewardable. The answer may be very large, return it after mod 10⁹ + 7.

A student attendance record is a string that only contains the following three characters:

‘A’ : Absent.
‘L’ : Late.
‘P’ : Present.

A record is regarded as rewardable if it doesn’t contain more than one ‘A’ (absent) or more than two continuous ‘L’ (late).

Example 1:

Input: n = 2
Output: 8 
Explanation:
There are 8 records with length 2 will be regarded as rewardable:
"PP" , "AP", "PA", "LP", "PL", "AL", "LA", "LL"
Only "AA" won't be regarded as rewardable owing to more than one absent times.

Note: The value of n won’t exceed 100,000.

Solution

C++

DFS w/ memorization (stack overflow)

class Solution {

public:

int checkRecord(int n) {

m_ = vector<vector<int>>(n + 1, vector<int>(6, 0));

if (n >= 100000) return 0;

return dfs(n, 1, 2);

}

private:

vector<vector<int>> m_;

// number of solutions of using at most A As and L Ls

long dfs(int n, int A, int L) {

if (n == 0) return 1;

int key = A * 3 + L;

if (m_[n][key]) return m_[n][key];

long ans = 0;

ans += dfs(n - 1, A, 2); // 'P', reset number of Ls

if (A > 0)

ans += dfs(n - 1, A - 1, 2); // 'A', reset number of Ls

if (L > 0)

ans += dfs(n - 1, A, L - 1); // 'L'

return m_[n][key] = (ans % 1000000007);

}

};

Time complexity: O(n)

Space complexity: O(1)

// Author: Huahua

// Running time: 129 ms

class Solution {

public:

int checkRecord(int n) {

constexpr int kMod = 1000000007;

vector<long> dp(6, 1);

for (int i = 1; i <= n; ++i) {

vector<long> tmp(6);

for (int A = 0; A <= 1; ++A)

for (int L = 0; L <= 2; ++L) {

const int key = getKey(A, L);

tmp[key] += dp[getKey(A, 2)];

if (A > 0) tmp[key] += dp[getKey(A - 1, 2)];

if (L > 0) tmp[key] += dp[getKey(A, L - 1)];

tmp[key] %= kMod;

}

dp.swap(tmp);

}

return dp[5];

}

private:

inline int getKey(int A, int L) { return A * 3 + L; }

};

花花酱 LeetCode 801. Minimum Swaps To Make Sequences Increasing

By zxi on March 17, 2018

Problem

题目大意：给你两个数组A, B。问最少需要多少次对应位置元素的交换才能使得A和B变成单调递增。

https://leetcode.com/problems/minimum-swaps-to-make-sequences-increasing/description/

We have two integer sequences A and B of the same non-zero length.

We are allowed to swap elements A[i] and B[i]. Note that both elements are in the same index position in their respective sequences.

At the end of some number of swaps, A and B are both strictly increasing. (A sequence is strictly increasing if and only if A[0] < A[1] < A[2] < ... < A[A.length - 1].)

Given A and B, return the minimum number of swaps to make both sequences strictly increasing. It is guaranteed that the given input always makes it possible.

Example:
Input: A = [1,3,5,4], B = [1,2,3,7]
Output: 1
Explanation: 
Swap A[3] and B[3].  Then the sequences are:
A = [1, 3, 5, 7] and B = [1, 2, 3, 4]
which are both strictly increasing.

Note:

A, B are arrays with the same length, and that length will be in the range [1, 1000].
A[i], B[i] are integer values in the range [0, 2000].

Solution: Search/DFS (TLE)

Time complexity: O(2^n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: TLE 84/102 test cases passed.

class Solution {

public:

int minSwap(vector<int>& A, vector<int>& B) {

int ans = INT_MAX;

dfs(A, B, 0, 0, ans);

return ans;

}

private:

void dfs(vector<int>& A, vector<int>& B, int i, int c, int& ans) {

if (c >= ans) return;

if (i == A.size()) {

ans = min(ans, c);

return;

}

if (i == 0 || A[i] > A[i - 1] && B[i] > B[i - 1])

dfs(A, B, i + 1, c, ans);

if (i == 0 || A[i] > B[i - 1] && B[i] > A[i - 1]) {

swap(A[i], B[i]);

dfs(A, B, i + 1, c + 1, ans);

swap(A[i], B[i]);

}

};

Solution: DP

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 15 ms

class Solution {

public:

int minSwap(vector<int>& A, vector<int>& B) {

const int n = A.size();

vector<int> keep(n, INT_MAX);

vector<int> swap(n, INT_MAX);

keep[0] = 0;

swap[0] = 1;

for (int i = 1; i < n; ++i) {

if (A[i] > A[i - 1] && B[i] > B[i - 1]) {

// Good case, no swapping needed.

keep[i] = keep[i - 1];

// Swapped A[i - 1] / B[i - 1], swap A[i], B[i] as well

swap[i] = swap[i - 1] + 1;

}

if (B[i] > A[i - 1] && A[i] > B[i - 1]) {

// A[i - 1] / B[i - 1] weren't swapped.

swap[i] = min(swap[i], keep[i - 1] + 1);

// Swapped A[i - 1] / B[i - 1], no swap needed for A[i] / B[i]

keep[i] = min(keep[i], swap[i - 1]);

}

return min(keep.back(), swap.back());

}

};

Python3

"""

Author: Huahua

Running time: 60 ms

"""

class Solution:

def minSwap(self, A, B):

n = len(A)

dp = [[float('inf'), float('inf')] for _ in range(n)]

dp[0][0], dp[0][1] = 0, 1

for i in range(1, n):

if A[i] > A[i - 1] and B[i] > B[i - 1]:

dp[i][0] = dp[i - 1][0]

dp[i][1] = dp[i - 1][1] + 1

if B[i] > A[i - 1] and A[i] > B[i - 1]:

dp[i][0] = min(dp[i][0], dp[i - 1][1])

dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1)

return min(dp[-1])

花花酱 LeetCode 413. Arithmetic Slices

By zxi on March 17, 2018

题目大意：返回所有子数组中等差数列的个数。

Problem

https://leetcode.com/problems/arithmetic-slices/description/

A sequence of number is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.

For example, these are arithmetic sequence:

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

The following sequence is not arithmetic.

1, 1, 2, 5, 7

A zero-indexed array A consisting of N numbers is given. A slice of that array is any pair of integers (P, Q) such that 0 <= P < Q < N.

A slice (P, Q) of array A is called arithmetic if the sequence:
A[P], A[p + 1], …, A[Q – 1], A[Q] is arithmetic. In particular, this means that P + 1 < Q.

The function should return the number of arithmetic slices in the array A.

Example:

A = [1, 2, 3, 4]

return: 3, for 3 arithmetic slices in A: [1, 2, 3], [2, 3, 4] and [1, 2, 3, 4] itself.

Solution 0: Reduction

Reduce the problem to # of all 1 sub arrays.

B[i – 2] = is_slice(A[i], A[i+1], A[i+2])

Time Complexity: O(n)

Space Complexity: O(n)

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numberOfArithmeticSlices(vector<int>& A) {

if (A.size() < 3) return 0;

vector<int> B(A.size() - 2, 0);

for (int i = 2; i < A.size() ; ++i) {

if (A[i - 1] - A[i - 2] == A[i] - A[i - 1])

B[i - 2] = 1;

}

return all1SubArrays(B);

}

private:

// return number of arrays whose values are all ones.

int all1SubArrays(const vector<int>& A) {

int sum = 0;

int curr = 0;

for (int i = 0; i < A.size(); ++i)

if (A[i]) sum += ++curr;

else curr = 0;

return sum;

}

};

Solution 1: Combined

C++

Time complexity: O(n)

Space complexity: O(1)

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numberOfArithmeticSlices(vector<int>& A) {

int sum = 0;

int curr = 0;

for (int i = 2; i < A.size() ; ++i) {

if (A[i - 1] - A[i - 2] == A[i] - A[i - 1]) {

sum += ++curr;

} else {

curr = 0;

}

return sum;

}

};

Posts tagged as “dp”

花花酱 LeetCode 818. Race Car

Problem

Visualization of the Solution

Solution 1: BFS

C++/Str

C++/Int

Solution 2: DP O(TlogT)

C++

Solution 3: DP O(T^2)

C++

C++/opt

Java

花花酱 LeetCode 813. Largest Sum of Averages

Problem

Idea

Init

Transition

Answer

Solution 1: DP

C++

C++ O(n) space

Solution 2: DFS + memoriation

C++

花花酱 LeetCode 552. Student Attendance Record II

Problem

Solution

花花酱 LeetCode 801. Minimum Swaps To Make Sequences Increasing

Problem

Solution: Search/DFS (TLE)

C++

Solution: DP

C++

Python3

花花酱 LeetCode 413. Arithmetic Slices

Problem

Example:

Solution 0: Reduction

Solution 1: Combined

Related Problems: