Posts tagged as “hard”

花花酱 LeetCode 1782. Count Pairs Of Nodes

By zxi on March 6, 2021

You are given an undirected graph represented by an integer n, which is the number of nodes, and edges, where edges[i] = [u_i, v_i] which indicates that there is an undirected edge between u_i and v_i. You are also given an integer array queries.

The answer to the j^th query is the number of pairs of nodes (a, b) that satisfy the following conditions:

a < b
cnt is strictly greater than queries[j], where cnt is the number of edges incident to a or b.

Return an array answers such that answers.length == queries.length and answers[j] is the answer of the j^th query.

Note that there can be repeated edges.

Example 1: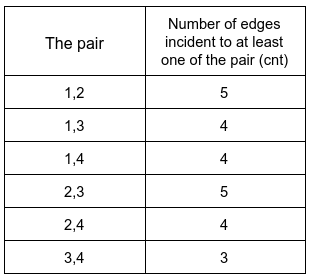

Input: n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
Output: [6,5]
Explanation: The number of edges incident to at least one of each pair is shown above.

Example 2:

Input: n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
Output: [10,10,9,8,6]

Constraints:

2 <= n <= 2 * 10⁴
1 <= edges.length <= 10⁵
1 <= u_i, v_i <= n
u_i!= v_i
1 <= queries.length <= 20
0 <= queries[j] < edges.length

Solution 1: Pre-compute

Pre-compute # of pairs with total edges >= k. where k is from 0 to max_degree * 2 + 1.

Time complexity: (|node_degrees|² + V + E)
Space complexity: O(V+E)

C++

// Author: huahua

class Solution {

public:

vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {

vector<int> node_degrees(n);

unordered_map<int, int> edge_freq;

for (auto& e : edges) {

sort(begin(e), end(e));

++node_degrees[--e[0]];

++node_degrees[--e[1]];

++edge_freq[(e[0] << 16) | e[1]];

}

const int max_degree = *max_element(begin(node_degrees),

end(node_degrees));

// Need pad one more to handle "not found / 0" case.

vector<int> counts(max_degree * 2 + 2);

unordered_map<int, int> degree_count;

for (int i = 0; i < n; ++i)

++degree_count[node_degrees[i]];

for (auto& [d1, c1] : degree_count)

for (auto& [d2, c2] : degree_count)

// Only count once if degrees are different to ensure (a < b)

if (d1 < d2) counts[d1 + d2] += c1 * c2;

// If degrees are the same C(n, 2) to ensure (a < b)

else if (d1 == d2) counts[d1 * 2] += c1 * (c1 - 1) / 2;

for (auto& [key, freq] : edge_freq) {

const int u = key >> 16;

const int v = key & 0xFFFF;

// For a pair of (u, v) their actual edge count is

// d[u] + d[v] - freq[(u, v)] instead of d[u] + d[v]

counts[node_degrees[u] + node_degrees[v]] -= 1;

counts[node_degrees[u] + node_degrees[v] - freq] += 1;

}

// counts[i] = # of pairs whose total edges >= i

for (int i = counts.size() - 2; i >= 0; --i)

counts[i] += counts[i + 1];

vector<int> ans;

for (int q : queries)

ans.push_back(counts[min(q + 1, static_cast<int>(counts.size() - 1))]);

return ans;

}

};

花花酱 LeetCode 1776. Car Fleet II

By zxi on February 27, 2021

There are n cars traveling at different speeds in the same direction along a one-lane road. You are given an array cars of length n, where cars[i] = [position_i, speed_i] represents:

position_i is the distance between the i^th car and the beginning of the road in meters. It is guaranteed that position_i < position_i+1.
speed_i is the initial speed of the i^th car in meters per second.

For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the slowest car in the fleet.

Return an array answer, where answer[i] is the time, in seconds, at which the i^th car collides with the next car, or -1 if the car does not collide with the next car. Answers within 10^-5 of the actual answers are accepted.

Example 1:

Input: cars = [[1,2],[2,1],[4,3],[7,2]]
Output: [1.00000,-1.00000,3.00000,-1.00000]
Explanation: After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.

Example 2:

Input: cars = [[3,4],[5,4],[6,3],[9,1]]
Output: [2.00000,1.00000,1.50000,-1.00000]

Constraints:

1 <= cars.length <= 10⁵
1 <= position_i, speed_i <= 10⁶
position_i < position_i+1

Solution: Monotonic Stack

Key observation: If my speed is slower than the speed of the previous car, not only mine but also all cars behind me will NEVER be able to catch/collide with the previous car. Such that we can throw it away.

Maintain a stack that stores the indices of cars with increasing speed.

Process car from right to left, for each car, pop the stack (throw the fastest car away) if any of the following conditions hold.
1) speed <= stack.top().speed
2) There are more than one car before me and it takes more than to collide the fastest car than time the fastest took to collide.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<double> getCollisionTimes(vector<vector<int>>& cars) {

auto collide = [&](int i, int j) -> double {

return static_cast<double>(cars[i][0] - cars[j][0]) /

(cars[j][1] - cars[i][1]);

};

const int n = cars.size();

vector<double> ans(n, -1);

stack<int> s;

for (int i = n - 1; i >= 0; --i) {

while (!s.empty() && (cars[i][1] <= cars[s.top()][1] ||

(s.size() > 1 && collide(i, s.top()) > ans[s.top()])))

s.pop();

ans[i] = s.empty() ? -1 : collide(i, s.top());

s.push(i);

}

return ans;

}

};

花花酱 LeetCode 1766. Tree of Coprimes

By zxi on February 20, 2021

There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. Each node has a value associated with it, and the root of the tree is node 0.

To represent this tree, you are given an integer array nums and a 2D array edges. Each nums[i] represents the i^th node’s value, and each edges[j] = [u_j, v_j] represents an edge between nodes u_j and v_j in the tree.

Two values x and y are coprime if gcd(x, y) == 1 where gcd(x, y) is the greatest common divisor of x and y.

An ancestor of a node i is any other node on the shortest path from node i to the root. A node is not considered an ancestor of itself.

Return an array ans of size n, where ans[i] is the closest ancestor to node i such that nums[i] and nums[ans[i]] are coprime, or -1 if there is no such ancestor.

Example 1:

Input: nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
Output: [-1,0,0,1]
Explanation: In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
  value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
  closest valid ancestor.

Example 2:

Input: nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: [-1,0,-1,0,0,0,-1]

Constraints:

nums.length == n
1 <= nums[i] <= 50
1 <= n <= 10⁵
edges.length == n - 1
edges[j].length == 2
0 <= u_j, v_j < n
u_j != v_j

Solution: DFS + Stack

Pre-compute for coprimes for each number.

For each node, enumerate all it’s coprime numbers, find the deepest occurrence.

Time complexity: O(n * max(nums))
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {

constexpr int kMax = 50;

const int n = nums.size();

vector<vector<int>> g(n);

for (const auto& e : edges) {

g[e[0]].push_back(e[1]);

g[e[1]].push_back(e[0]);

}

vector<vector<int>> coprime(kMax + 1);

for (int i = 1; i <= kMax; ++i)

for (int j = 1; j <= kMax; ++j)

if (gcd(i, j) == 1) coprime[i].push_back(j);

vector<int> ans(n, INT_MAX);

vector<vector<pair<int, int>>> p(kMax + 1);

function<void(int, int)> dfs = [&](int cur, int d) {

int max_d = -1;

int ancestor = -1;

for (int co : coprime[nums[cur]])

if (!p[co].empty() && p[co].back().first > max_d) {

max_d = p[co].back().first;

ancestor = p[co].back().second;

}

ans[cur] = ancestor;

p[nums[cur]].emplace_back(d, cur);

for (int nxt : g[cur])

if (ans[nxt] == INT_MAX) dfs(nxt, d + 1);

p[nums[cur]].pop_back();

};

dfs(0, 0);

return ans;

}

};

花花酱 LeetCode 1761. Minimum Degree of a Connected Trio in a Graph

By zxi on February 13, 2021

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [u_i, v_i] indicates that there is an undirected edge between u_i and v_i.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1:

Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2:

Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

Constraints:

2 <= n <= 400
edges[i].length == 2
1 <= edges.length <= n * (n-1) / 2
1 <= u_i, v_i <= n
u_i!= v_i
There are no repeated edges.

Solution: Brute Force

Try all possible Trios.

Time complexity: O(n^3)
Space complexity: O(n^2)

C++

// Author: Huahua

class Solution {

public:

int minTrioDegree(int n, vector<vector<int>>& edges) {

vector<bitset<400>> g(n);

for (const auto& e : edges) {

g[e[0] - 1].set(e[1] - 1);

g[e[1] - 1].set(e[0] - 1);

}

size_t ans = INT_MAX;

for (int i = 0; i < n; ++i)

for (int j = i + 1; j < n; ++j)

if (g[i][j])

for (int k = j + 1; k < n; ++k)

if (g[i][k] && g[j][k])

ans = min(ans, g[i].count() + g[j].count() + g[k].count() - 6);

return ans == INT_MAX ? -1 : ans;

}

};

花花酱 LeetCode 1751. Maximum Number of Events That Can Be Attended II

By zxi on February 6, 2021

You are given an array of events where events[i] = [startDay_i, endDay_i, value_i]. The i^th event starts at startDay_iand ends at endDay_i, and if you attend this event, you will receive a value of value_i. You are also given an integer k which represents the maximum number of events you can attend.

You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.

Return the maximum sum of values that you can receive by attending events.

Example 1:

Input: events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
Output: 7
Explanation: Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.

Example 2:

Input: events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
Output: 10
Explanation: Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do not have to attend k events.

Example 3:

Input: events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
Output: 9
Explanation: Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.

Constraints:

1 <= k <= events.length
1 <= k * events.length <= 10⁶
1 <= startDay_i <= endDay_i <= 10⁹
1 <= value_i <= 10⁶

Solution: DP + Binary Search

Sort events by ending time.
dp[i][j] := max value we can get by attending at most j events among events[0~i].
dp[i][j] = max(dp[i – 1][j], dp[p][j – 1] + value[i])
p is the first event that does not overlap with the current one.

Time complexity: O(nlogn + nk)
Space complexity: O(nk)

C++

// Author: Huahua

class Solution {

public:

int maxValue(vector<vector<int>>& events, int k) {

const int n = events.size();

vector<vector<int>> dp(n + 1, vector<int>(k + 1));

vector<int> e(n);

auto comp = [](const vector<int>& a, const vector<int>& b) {

return a[1] < b[1];

};

sort(begin(events), end(events), comp);

for (int i = 1; i <= n; ++i) {

const int p = lower_bound(begin(events),

begin(events) + i,

vector<int>{0, events[i - 1][0], 0},

comp) - begin(events);

for (int j = 1; j <= k; ++j)

dp[i][j] = max(dp[i - 1][j],

dp[p][j - 1] + events[i - 1][2]);

}

return dp[n][k];

}

};