Posts tagged as “hard”

花花酱 LeetCode 2251. Number of Flowers in Full Bloom

By zxi on April 27, 2022

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [start_i, end_i] means the i^th flower will be in full bloom from start_i to end_i (inclusive). You are also given a 0-indexed integer array persons of size n, where persons[i] is the time that the i^th person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the i^th person arrives.

Example 1:

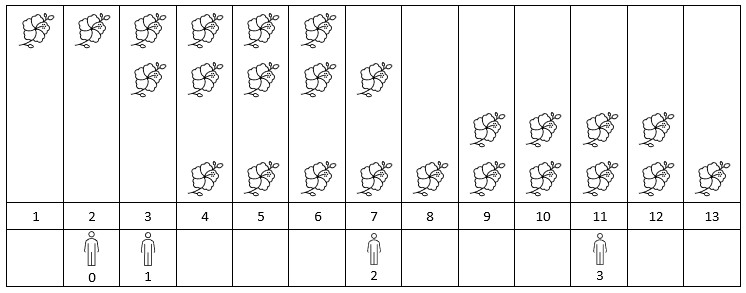
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

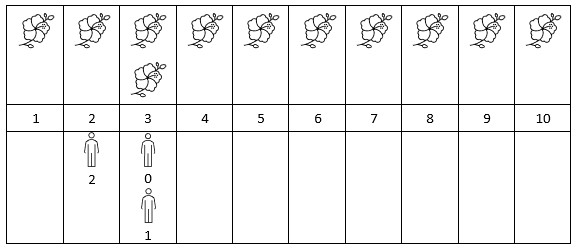
Input: flowers = [[1,10],[3,3]], persons = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10⁴
flowers[i].length == 2
1 <= start_i <= end_i <= 10⁹
1 <= persons.length <= 5 * 10⁴
1 <= persons[i] <= 10⁹

Solution: Prefix Sum + Binary Search

Use a treemap to store the counts (ordered by time t), when a flower begins to bloom at start, we increase m[start], when it dies at end, we decrease m[end+1]. prefix_sum[t] indicates the # of blooming flowers at time t.

For each people, use binary search to find the latest # of flowers before his arrival.

Time complexity: O(nlogn + mlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {

map<int, int> m{{0, 0}};

for (const auto& f : flowers)

++m[f[0]], --m[f[1] + 1];

int sum = 0;

for (auto& [t, c] : m)

c = sum += c;

vector<int> ans;

for (int t : persons)

ans.push_back(prev(m.upper_bound(t))->second);

return ans;

}

};

花花酱 LeetCode 2242. Maximum Score of a Node Sequence

By zxi on April 16, 2022

There is an undirected graph with n nodes, numbered from 0 to n - 1.

You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

A node sequence is valid if it meets the following conditions:

There is an edge connecting every pair of adjacent nodes in the sequence.
No node appears more than once in the sequence.

The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return -1.

Example 1:

Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

Example 2:

Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.

Constraints:

n == scores.length
4 <= n <= 5 * 10⁴
1 <= scores[i] <= 10⁸
0 <= edges.length <= 5 * 10⁴
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no duplicate edges.

Solution: Greedy / Top3 neighbors

Since |E| is already 5*10⁴, we can’t enumerate all possible sequences. We must do in O(|E|) or O(|E|log|E|).

Enumerate all the edges, we have a pair of node a, b. To get the optimal answer, we just need to find the largest neighbor of a and b, which we call c, d respectively. Just need to make sure a, b, c, d are unique. i.e. c != d, c != b and d != a. Since the a’s largest neighbor can be either b or d. We can’t just store the largest neighbor, but top 3 instead for each node to avoid duplications.

Time complexity: O(|E|*9)
Space complexity: O(|V|*3)

C++

// Author: Huahua

class Solution {

public:

int maximumScore(vector<int>& scores, vector<vector<int>>& edges) {

const int n = scores.size();

vector<set<pair<int, int>>> top3(n);

for (const auto& e : edges) {

top3[e[0]].emplace(scores[e[1]], e[1]);

top3[e[1]].emplace(scores[e[0]], e[0]);

if (top3[e[0]].size() > 3) top3[e[0]].erase(begin(top3[e[0]]));

if (top3[e[1]].size() > 3) top3[e[1]].erase(begin(top3[e[1]]));

}

int ans = -1;

for (const auto& e : edges) {

const int a = e[0], b = e[1], sa = scores[a], sb = scores[b];

for (const auto& [sc, c] : top3[a])

for (const auto& [sd, d] : top3[b])

if (sa + sb + sc + sd > ans && c != b && c != d && d != a)

ans = sa + sb + sc + sd;

}

return ans;

}

};

花花酱 LeetCode 2227. Encrypt and Decrypt Strings

By zxi on April 3, 2022

You are given a character array keys containing unique characters and a string array values containing strings of length 2. You are also given another string array dictionary that contains all permitted original strings after decryption. You should implement a data structure that can encrypt or decrypt a 0-indexed string.

A string is encrypted with the following process:

For each character c in the string, we find the index i satisfying keys[i] == c in keys.
Replace c with values[i] in the string.

A string is decrypted with the following process:

For each substring s of length 2 occurring at an even index in the string, we find an i such that values[i] == s. If there are multiple valid i, we choose any one of them. This means a string could have multiple possible strings it can decrypt to.
Replace s with keys[i] in the string.

Implement the Encrypter class:

Encrypter(char[] keys, String[] values, String[] dictionary) Initializes the Encrypter class with keys, values, and dictionary.
String encrypt(String word1) Encrypts word1 with the encryption process described above and returns the encrypted string.
int decrypt(String word2) Returns the number of possible strings word2 could decrypt to that also appear in dictionary.

Example 1:

Input
["Encrypter", "encrypt", "decrypt"]
[[['a', 'b', 'c', 'd'], ["ei", "zf", "ei", "am"], ["abcd", "acbd", "adbc", "badc", "dacb", "cadb", "cbda", "abad"]], ["abcd"], ["eizfeiam"]]
Output

[null, “eizfeiam”, 2]

Explanation Encrypter encrypter = new Encrypter([[‘a’, ‘b’, ‘c’, ‘d’], [“ei”, “zf”, “ei”, “am”], [“abcd”, “acbd”, “adbc”, “badc”, “dacb”, “cadb”, “cbda”, “abad”]); encrypter.encrypt(“abcd”); // return “eizfeiam”. // ‘a’ maps to “ei”, ‘b’ maps to “zf”, ‘c’ maps to “ei”, and ‘d’ maps to “am”. encrypter.decrypt(“eizfeiam”); // return 2. // “ei” can map to ‘a’ or ‘c’, “zf” maps to ‘b’, and “am” maps to ‘d’. // Thus, the possible strings after decryption are “abad”, “cbad”, “abcd”, and “cbcd”. // 2 of those strings, “abad” and “abcd”, appear in dictionary, so the answer is 2.

Constraints:

1 <= keys.length == values.length <= 26
values[i].length == 2
1 <= dictionary.length <= 100
1 <= dictionary[i].length <= 100
All keys[i] and dictionary[i] are unique.
1 <= word1.length <= 2000
1 <= word2.length <= 200
All word1[i] appear in keys.
word2.length is even.
keys, values[i], dictionary[i], word1, and word2 only contain lowercase English letters.
At most 200 calls will be made to encrypt and decrypt in total.

Solution:

For encryption, follow the instruction. Time complexity: O(len(word)) = O(2000)
For decryption, try all words in the dictionary and encrypt them and compare the encrypted string with the word to decrypt. Time complexity: O(sum(len(word_in_dict))) = O(100*100)

Worst case: 200 calls to decryption, T = 200 * O(100 * 100) = O(2*10⁶)

C++

// Author: Huahua

class Encrypter {

public:

Encrypter(vector<char>& keys,

vector<string>& values,

vector<string>& dictionary):

vals(26),

dict(dictionary) {

for (size_t i = 0; i < keys.size(); ++i)

vals[keys[i] - 'a'] = values[i];

}

string encrypt(string word1) {

string ans;

for (char c : word1)

ans += vals[c - 'a'];

return ans;

}

int decrypt(string word2) {

return count_if(begin(dict), end(dict), [&](const string& w){

return encrypt(w) == word2;

});

}

private:

vector<string> vals;

vector<string> dict;

};

Optimization

Pre-compute answer for all the words in dictionary.

decrypt: Time complexity: O(1)

C++

// Author: Huahua

class Encrypter {

public:

Encrypter(vector<char>& keys,

vector<string>& values,

vector<string>& dictionary):

vals(26) {

for (size_t i = 0; i < keys.size(); ++i)

vals[keys[i] - 'a'] = values[i];

for (const string& w : dictionary)

++counts[encrypt(w)];

}

string encrypt(string word1) {

string ans;

for (char c : word1)

ans += vals[c - 'a'];

return ans;

}

int decrypt(string word2) {

auto it = counts.find(word2);

return it == counts.end() ? 0 : it->second;

}

private:

vector<string> vals;

unordered_map<string, int> counts;

};

花花酱 LeetCode 2223. Sum of Scores of Built Strings

By zxi on April 2, 2022

You are building a string s of length n one character at a time, prepending each new character to the front of the string. The strings are labeled from 1 to n, where the string with length i is labeled s_i.

For example, for s = "abaca", s₁ == "a", s₂ == "ca", s₃ == "aca", etc.

The score of s_i is the length of the longest common prefix between s_i and s_n (Note that s == s_n).

Given the final string s, return the sum of the score of every s_i.

Example 1:

Input: s = "babab"
Output: 9
Explanation:
For s₁ == "b", the longest common prefix is "b" which has a score of 1.
For s₂ == "ab", there is no common prefix so the score is 0.
For s₃ == "bab", the longest common prefix is "bab" which has a score of 3.
For s₄ == "abab", there is no common prefix so the score is 0.
For s₅ == "babab", the longest common prefix is "babab" which has a score of 5.
The sum of the scores is 1 + 0 + 3 + 0 + 5 = 9, so we return 9.

Example 2:

Input: s = "azbazbzaz"
Output: 14
Explanation: 
For s₂ == "az", the longest common prefix is "az" which has a score of 2.
For s₆ == "azbzaz", the longest common prefix is "azb" which has a score of 3.
For s₉ == "azbazbzaz", the longest common prefix is "azbazbzaz" which has a score of 9.
For all other s_i, the score is 0.
The sum of the scores is 2 + 3 + 9 = 14, so we return 14.

Constraints:

1 <= s.length <= 10⁵
s consists of lowercase English letters.

Solution: Z-Function

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

long long sumScores(string s) {

auto zFunc = [](string_view s) {

const int n = s.length();

vector<long long> z(n);

for (long long i = 1, l = 0, r = 0; i < n; ++i) {

if (i <= r)

z[i] = min(r - i + 1, z[i - l]);

while (i + z[i] < n && s[z[i]] == s[i + z[i]])

++z[i];

if (i + z[i] - 1 > r) {

l = i;

r = i + z[i] - 1;

}

return accumulate(begin(z), end(z), 0LL);

};

return zFunc(s) + s.length();

}

};

花花酱 LeetCode 2218. Maximum Value of K Coins From Piles

By zxi on March 28, 2022

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the i^th pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Example 1:

Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

n == piles.length
1 <= n <= 1000
1 <= piles[i][j] <= 10⁵
1 <= k <= sum(piles[i].length) <= 2000

Solution: DP

let dp(i, k) be the maximum value of picking k elements using piles[i:n].

dp(i, k) = max(dp(i + 1, k), sum(piles[i][0~j]) + dp(i + 1, k – j – 1)), 0 <= j < len(piles[i])

Time complexity: O(n * m), m = sum(piles[i]) <= 2000
Space complexity: O(n * k)

Python

# Author: Huahua

class Solution:

def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:

n = len(piles)

@cache

def dp(i: int, k: int) -> int:

"""Max value of picking k elements using piles[i:n]."""

if i == n: return 0

ans, cur = dp(i + 1, k), 0

for j in range(min(len(piles[i]), k)):

ans = max(ans, (cur := cur + piles[i][j]) + dp(i + 1, k - j - 1))

return ans

return dp(0, k)