Posts tagged as “O(mn)”

花花酱 LeetCode 1267. Count Servers that Communicate

By zxi on November 23, 2019

You are given a map of a server center, represented as a m * n integer matrix grid, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.

Return the number of servers that communicate with any other server.

Example 1:

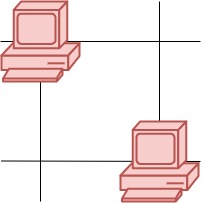
Input: grid = [[1,0],[0,1]]
Output: 0
Explanation: No servers can communicate with others.

Example 2:

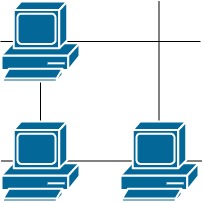
Input: grid = [[1,0],[1,1]]
Output: 3
Explanation: All three servers can communicate with at least one other server.

Example 3:

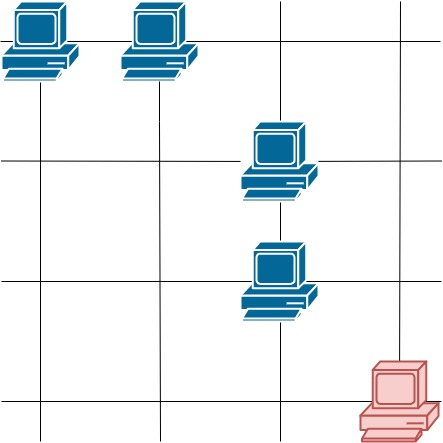
Input: grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]]
Output: 4
Explanation: The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.

Constraints:

m == grid.length
n == grid[i].length
1 <= m <= 250
1 <= n <= 250
grid[i][j] == 0 or 1

Solution: Counting

Two passes:
First pass, count number of computers for each row and each column.
Second pass, count grid[i][j] if rows[i] or cols[j] has more than 1 computer.

Time complexity: O(m*n)
Space complexity: O(m + n)

C++

// Author: Huahua

class Solution {

public:

int countServers(vector<vector<int>>& grid) {

const size_t m = grid.size();

const size_t n = grid[0].size();

vector<int> rows(m);

vector<int> cols(n);

for (size_t i = 0; i < m; ++i)

for (size_t j = 0; j < n; ++j) {

rows[i] += grid[i][j];

cols[j] += grid[i][j];

}

int ans = 0;

for (size_t i = 0; i < m; ++i)

for (size_t j = 0; j < n; ++j)

ans += (rows[i] > 1 || cols[j] > 1) ? grid[i][j] : 0;

return ans;

}

};

花花酱 LeetCode 1237. Find Positive Integer Solution for a Given Equation

By zxi on October 27, 2019

Given a function f(x, y) and a value z, return all positive integer pairs x and y where f(x,y) == z.

The function is constantly increasing, i.e.:

f(x, y) < f(x + 1, y)
f(x, y) < f(x, y + 1)

The function interface is defined like this:

interface CustomFunction {
public:
  // Returns positive integer f(x, y) for any given positive integer x and y.
  int f(int x, int y);
};

For custom testing purposes you’re given an integer function_id and a target z as input, where function_id represent one function from an secret internal list, on the examples you’ll know only two functions from the list.

You may return the solutions in any order.

Example 1:

Input: function_id = 1, z = 5
Output: [[1,4],[2,3],[3,2],[4,1]]
Explanation: function_id = 1 means that f(x, y) = x + y

Example 2:

Input: function_id = 2, z = 5
Output: [[1,5],[5,1]]
Explanation: function_id = 2 means that f(x, y) = x * y

Constraints:

1 <= function_id <= 9
1 <= z <= 100
It’s guaranteed that the solutions of f(x, y) == z will be on the range 1 <= x, y <= 1000
It’s also guaranteed that f(x, y) will fit in 32 bit signed integer if 1 <= x, y <= 1000

Solution1 : Brute Force

Time complexity: O(1000*1000)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {

vector<vector<int>> ans;

for (int x = 1; x <= 1000; ++x) {

if (customfunction.f(x, 1) > z) break;

for (int y = 1; y <= 1000; ++y) {

int t = customfunction.f(x, y);

if (t > z) break;

if (t == z) ans.push_back({x, y});

}

return ans;

}

};

花花酱 LeetCode 130. Surrounded Regions

By zxi on October 9, 2019

Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example:

X X X X
X O O X
X X O X
X O X X

After running your function, the board should be:

X X X X
X X X X
X X X X
X O X X

Explanation:

Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Solution: DFS

Time complexity: O(m*n)
Space complexity: O(m*n)

Only starts DFS at border cells of O.

C++

// Author: Huahua

class Solution {

public:

void solve(vector<vector<char>>& board) {

const int m = board.size();

if (m == 0) return;

const int n = board[0].size();

function<void(int, int)> dfs = [&](int x, int y) {

if (x < 0 || x >= n || y < 0 || y >= m || board[y][x] != 'O') return;

board[y][x] = 'G'; // mark it as good

dfs(x - 1, y);

dfs(x + 1, y);

dfs(x, y - 1);

dfs(x, y + 1);

};

for (int y = 0; y < m; ++y)

dfs(0, y), dfs(n - 1, y);

for (int x = 0; x < n; ++x)

dfs(x, 0), dfs(x, m - 1);

map<char, char> v{{'G','O'},{'O','X'}, {'X','X'}};

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

board[y][x] = v[board[y][x]];

}

};

花花酱 LeetCode 1143. Longest Common Subsequence

By zxi on August 29, 2019

Given two strings text1 and text2, return the length of their longest common subsequence.

A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, “ace” is a subsequence of “abcde” while “aec” is not). A common subsequence of two strings is a subsequence that is common to both strings.

If there is no common subsequence, return 0.

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

1 <= text1.length <= 1000
1 <= text2.length <= 1000
The input strings consist of lowercase English characters only.

Solution: DP

Use dp[i][j] to represent the length of longest common sub-sequence of text1[0:i] and text2[0:j]
dp[i][j] = dp[i – 1][j – 1] + 1 if text1[i – 1] == text2[j – 1] else max(dp[i][j – 1], dp[i – 1][j])

Time complexity: O(mn)
Space complexity: O(mn) -> O(n)

C++

// Author: Huahua, 16ms 14.9 MB

class Solution {

public:

int longestCommonSubsequence(string text1, string text2) {

int m = text1.length();

int n = text2.length();

vector<vector<int>> dp(m + 1, vector<int>(n + 1));

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

if (text1[i] == text2[j])

dp[i + 1][j + 1] = dp[i][j] + 1;

else

dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]);

return dp[m][n];

}

};

C++/V2

// Author: Huahua, 8ms, 8.8MB

class Solution {

public:

int longestCommonSubsequence(string text1, string text2) {

int m = text1.length();

int n = text2.length();

vector<int> dp(n + 1);

for (int i = 0; i < m; ++i) {

int prev = 0; // dp[i][j]

for (int j = 0; j < n; ++j) {

int curr = dp[j + 1]; // dp[i][j + 1]

if (text1[i] == text2[j])

// dp[i + 1][j + 1] = dp[i][j] + 1

dp[j + 1] = prev + 1;

else

// dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j])

dp[j + 1] = max(curr, dp[j]);

prev = curr;

}

return dp[n]; // dp[m][n]

}

};

C++/V3

// Author: Huahua

class Solution {

public:

int longestCommonSubsequence(string text1, string text2) {

int m = text1.length();

int n = text2.length();

vector<int> dp1(n + 1);

vector<int> dp2(n + 1);

for (int i = 0; i < m; ++i) {

for (int j = 0; j < n; ++j)

if (text1[i] == text2[j])

dp2[j + 1] = dp1[j] + 1;

else

dp2[j + 1] = max(dp1[j + 1], dp2[j]);

swap(dp1, dp2);

}

return dp1[n];

}

};

花花酱 LeetCode 463. Island Perimeter

By zxi on August 17, 2018

Problem

You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 represents water. Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells). The island doesn’t have “lakes” (water inside that isn’t connected to the water around the island). One cell is a square with side length 1. The grid is rectangular, width and height don’t exceed 100. Determine the perimeter of the island.

Example:

[[0,1,0,0],
 [1,1,1,0],
 [0,1,0,0],
 [1,1,0,0]]

Answer: 16
Explanation: The perimeter is the 16 yellow stripes in the image below:

Solution: Counting

If a land has 0 neighbour, it contributes 4 to the perimeter

If a land has 1 neighbour, it contributes 3 to the perimeter

If a land has 2 neighbours, it contributes 2 to the perimeter

If a land has 3 neighbours, it contributes 1 to the perimeter

If a land has 4 neighbours, it contributes 0 to the perimeter

perimeter = area * 4 – total_neighbours

Time complexity: O(mn)

Space complexity: O(1)

// Author: Huahua

// Running time: 148 ms

class Solution {

public:

int islandPerimeter(vector<vector<int>>& grid) {

if (grid.empty()) return 0;

int m = grid.size();

int n = grid[0].size();

int area = 0;

int conn = 0;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

if (grid[y][x] == 1) {

++area;

if (y > 0 && grid[y - 1][x] == 1) ++conn;

if (x > 0 && grid[y][x - 1] == 1) ++conn;

}

return area*4 - conn*2;

}

};