Posts tagged as “stack”

花花酱 LeetCode 901. Online Stock Span

By zxi on September 14, 2018

Problem

Write a class StockSpanner which collects daily price quotes for some stock, and returns the span of that stock’s price for the current day.

The span of the stock’s price today is defined as the maximum number of consecutive days (starting from today and going backwards) for which the price of the stock was less than or equal to today’s price.

For example, if the price of a stock over the next 7 days were [100, 80, 60, 70, 60, 75, 85], then the stock spans would be [1, 1, 1, 2, 1, 4, 6].

Example 1:

Input: ["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
Output: [null,1,1,1,2,1,4,6]
Explanation: 
First, S = StockSpanner() is initialized.  Then:
S.next(100) is called and returns 1,
S.next(80) is called and returns 1,
S.next(60) is called and returns 1,
S.next(70) is called and returns 2,
S.next(60) is called and returns 1,
S.next(75) is called and returns 4,
S.next(85) is called and returns 6.

Note that (for example) S.next(75) returned 4, because the last 4 prices
(including today's price of 75) were less than or equal to today's price.

Note:

Calls to StockSpanner.next(int price) will have 1 <= price <= 10^5.
There will be at most 10000 calls to StockSpanner.next per test case.
There will be at most 150000 calls to StockSpanner.next across all test cases.
The total time limit for this problem has been reduced by 75% for C++, and 50% for all other languages.

Solution 1: Brute Force (TLE)

Time complexity: O(n) per next call

Space complexity: O(n)

Solution 2: DP

dp[i] := span of prices[i]

j = i – 1
while j >= 0 and prices[i] >= prices[j]: j -= dp[j]
dp[i] = i – j

C++

// Author: Huahua, 144 ms

class StockSpanner {

public:

StockSpanner() {}

int next(int price) {

if (prices_.empty() || price < prices_.back()) {

dp_.push_back(1);

} else {

int j = prices_.size() - 1;

while (j >= 0 && price >= prices_[j]) {

j -= dp_[j];

}

dp_.push_back(prices_.size() - j);

}

prices_.push_back(price);

return dp_.back();

}

private:

vector<int> dp_;

vector<int> prices_;

};

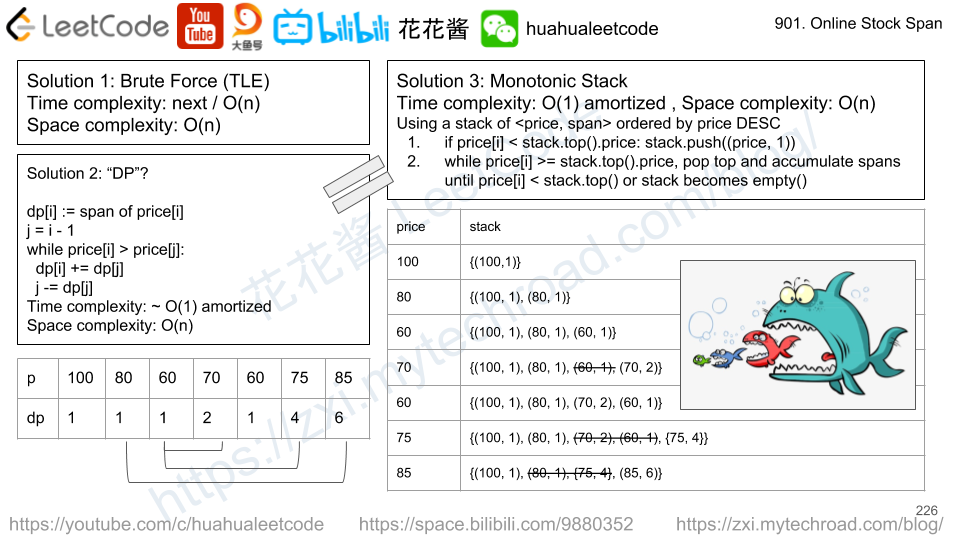
Solution 3: Monotonic Stack

Maintain a monotonic stack whose element are pairs of <price, span>, sorted by price from high to low.

When a new price comes in

If it’s less than top price, add a new pair (price, 1) to the stack, return 1
If it’s greater than top element, collapse the stack and accumulate the span until the top price is higher than the new price. return the total span

e.g. prices: 10, 6, 5, 4, 3, 7

after 3, the stack looks [(10,1), (6,1), (5,1), (4,1), (3, 1)],

when 7 arrives, [(10,1), ~~(6,1), (5,1), (4,1), (3, 1),~~ (7, 4 + 1)] = [(10, 1), (7, 5)]

Time complexity: O(1) amortized, each element will be pushed on to stack once, and pop at most once.

Space complexity: O(n), in the worst case, the prices is in descending order.

C++

// Author: Huahua

class StockSpanner {

public:

StockSpanner() {}

int next(int price) {

int span = 1;

while (!s_.empty() && price >= s_.top().first) {

span += s_.top().second;

s_.pop();

}

s_.emplace(price, span);

return span;

}

private:

stack<pair<int, int>> s_; // {price, span}, ordered by price DESC.

};

Java

// Author: Huahua

class StockSpanner {

private Stack<Integer> prices;

private Stack<Integer> spans;

public StockSpanner() {

prices = new Stack<>();

spans = new Stack<>();

}

public int next(int price) {

int span = 1;

while (!prices.empty() && price >= prices.peek()) {

span += spans.pop();

prices.pop();

}

prices.push(price);

spans.push(span);

return span;

}

Python3

# Author: Huahua

class StockSpanner:

def __init__(self):

self.s = list()

def next(self, price):

span = 1

while self.s and price >= self.s[-1][0]:

span += self.s[-1][1]

self.s.pop()

self.s.append((price, span))

return span

Problem

Implement FreqStack, a class which simulates the operation of a stack-like data structure.

FreqStack has two functions:

push(int x), which pushes an integer x onto the stack.
pop(), which removes and returns the most frequent element in the stack.
- If there is a tie for most frequent element, the element closest to the top of the stack is removed and returned.

Example 1:

Input: 
["FreqStack","push","push","push","push","push","push","pop","pop","pop","pop"],
[[],[5],[7],[5],[7],[4],[5],[],[],[],[]]
Output: [null,null,null,null,null,null,null,5,7,5,4]
Explanation:
After making six .push operations, the stack is [5,7,5,7,4,5] from bottom to top.  Then:

pop() -> returns 5, as 5 is the most frequent.
The stack becomes [5,7,5,7,4].

pop() -> returns 7, as 5 and 7 is the most frequent, but 7 is closest to the top.
The stack becomes [5,7,5,4].

pop() -> returns 5.
The stack becomes [5,7,4].

pop() -> returns 4.
The stack becomes [5,7].

Note:

Calls to FreqStack.push(int x) will be such that 0 <= x <= 10^9.
It is guaranteed that FreqStack.pop() won’t be called if the stack has zero elements.
The total number of FreqStack.push calls will not exceed 10000 in a single test case.
The total number of FreqStack.pop calls will not exceed 10000 in a single test case.
The total number of FreqStack.push and FreqStack.pop calls will not exceed 150000 across all test cases.

Solution 1: Buckets

We have n stacks. The i-th stack has the of elements with freq i when pushed.

We keep tracking the freq of each element.

push(x): stacks[++freq(x)].push(x) # inc x’s freq and push it onto freq-th stack

pop(): x = stacks[max_freq].pop(), –freq(x); # pop element x from the max_freq stack and dec it’s freq.

Time complexity: O(1) push / pop

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 144 ms

class FreqStack {

public:

FreqStack() {}

void push(int x) {

auto it = freq_.find(x);

if (it == freq_.end())

it = freq_.emplace(x, 0).first;

int freq = ++it->second;

if (stacks_.size() < freq) stacks_.push_back({});

stacks_[freq - 1].push(x);

}

int pop() {

int x = stacks_.back().top();

stacks_.back().pop();

if (stacks_.back().empty())

stacks_.pop_back();

auto it = freq_.find(x);

if (!(--it->second))

freq_.erase(it);

return x;

}

private:

vector<stack<int>> stacks_;

unordered_map<int, int> freq_;

};

Solution2: Priority Queue

Use a max heap with key: (freq, seq), the max freq and closest to the top of stack element will be extracted first.

Time complexity: O(logn)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 132 ms

class FreqStack {

public:

FreqStack() {}

void push(int x) {

int key = (++f_[x] << 16) | (++seq_);

q_.emplace(key, x);

}

int pop() {

int x = q_.top().second; q_.pop();

if (--f_[x] == 0)

f_.erase(x);

return x;

}

private:

int seq_ = 0;

unordered_map<int, int> f_; // {x -> freq}

priority_queue<pair<int, int>> q_; // {freq | seq_, x}

};

Problem

Given a list of daily temperatures, produce a list that, for each day in the input, tells you how many days you would have to wait until a warmer temperature. If there is no future day for which this is possible, put 0 instead.

For example, given the list temperatures = [73, 74, 75, 71, 69, 72, 76, 73], your output should be [1, 1, 4, 2, 1, 1, 0, 0].

Note: The length of temperatures will be in the range [1, 30000]. Each temperature will be an integer in the range [30, 100].

Solution: Stack

Use a stack to track indices of future warmer days. From top to bottom: recent to far away.

Time complexity: O(n)

Space complexity: O(n)

// Author: Huahua

// Running time: 148 ms

class Solution {

public:

vector<int> dailyTemperatures(vector<int>& temperatures) {

const int n = temperatures.size();

stack<int> s;

vector<int> ans(n);

for (int i = n - 1; i >= 0; --i) {

while (!s.empty() && temperatures[s.top()] <= temperatures[i]) s.pop();

ans[i] = s.empty() ? 0 : s.top() - i;

s.push(i);

}

return ans;

}

};

花花酱 LeetCode 856. Score of Parentheses

By zxi on June 26, 2018

Problem

Given a balanced parentheses string S, compute the score of the string based on the following rule:

() has score 1
AB has score A + B, where A and B are balanced parentheses strings.
(A) has score 2 * A, where A is a balanced parentheses string.

Example 1:

Input: "()"
Output: 1

Example 2:

Input: "(())"
Output: 2

Example 3:

Input: "()()"
Output: 2

Example 4:

Input: "(()(()))"
Output: 6

Solution1: Recursion

Time complexity: O(n^2)

Space complexity: O(n)

// Author: Huahua

// Running time: 4ms

class Solution {

public:

int scoreOfParentheses(string S) {

return score(S, 0, S.length() - 1);

}

private:

int score(const string& S, int l, int r) {

if (r - l == 1) return 1; // "()"

int b = 0;

for (int i = l; i < r; ++i) {

if (S[i] == '(') ++b;

if (S[i] == ')') --b;

if (b == 0) // balanced

// score("(A)(B)") = score("(A)") + score("(B)")

return score(S, l, i) + score(S, i + 1, r);

}

// score("(A)") = 2 * score("A")

return 2 * score(S, l + 1, r - 1);

}

};

Solution2: Counting

Time complexity: O(n)

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int scoreOfParentheses(string S) {

int ans = 0;

int d = -1;

for (int i = 0; i < S.length(); ++i) {

d += S[i] == '(' ? 1 : -1;

if (S[i] == '(' && S[i + 1] == ')')

ans += 1 << d;

}

return ans;

}

};

Posts tagged as “stack”

花花酱 LeetCode 901. Online Stock Span

Problem

Solution 1: Brute Force (TLE)

Solution 2: DP

C++

Solution 3: Monotonic Stack

C++

Java

Python3

Related Problems

花花酱 LeetCode 895. Maximum Frequency Stack

Problem

Solution 1: Buckets

C++

Solution2: Priority Queue

C++

Related Problems

花花酱 LeetCode 739. Daily Temperatures

Problem

Solution: Stack

花花酱 LeetCode 856. Score of Parentheses

Problem

Solution1: Recursion

Solution2: Counting

Posts tagged as “stack”

花花酱 LeetCode 901. Online Stock Span

Problem

Solution 1: Brute Force (TLE)

Solution 2: DP

C++

Solution 3: Monotonic Stack

C++

Java

Python3

Related Problems

花花酱 LeetCode 895. Maximum Frequency Stack

Problem

Solution 1: Buckets

C++

Solution2: Priority Queue

C++

Related Problems

花花酱 LeetCode 739. Daily Temperatures

Problem

Solution: Stack

花花酱 LeetCode 445. Add Two Numbers II

Problem

Solution: Simulation

Related Problems

花花酱 LeetCode 856. Score of Parentheses

Problem

Solution1: Recursion

Solution2: Counting