Given a tree (i.e. a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. The root of the tree is the node 0, and each node of the tree has a label which is a lower-case character given in the string labels (i.e. The node with the number i has the label labels[i]).
The edges array is given on the form edges[i] = [ai, bi], which means there is an edge between nodes ai and bi in the tree.
Return an array of size n where ans[i] is the number of nodes in the subtree of the ith node which have the same label as node i.
A subtree of a tree T is the tree consisting of a node in T and all of its descendant nodes.
Example 1:
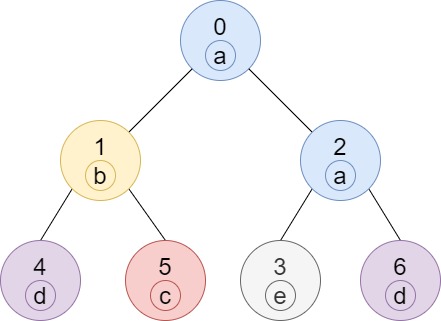
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd" Output: [2,1,1,1,1,1,1] Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree. Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
Example 2:
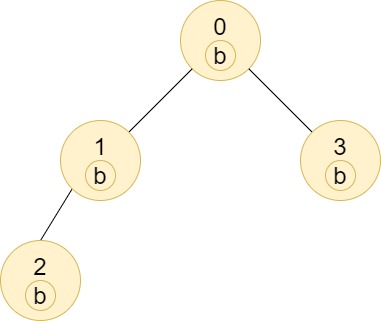
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb" Output: [4,2,1,1] Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1. The sub-tree of node 3 contains only node 3, so the answer is 1. The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2. The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
Example 3:
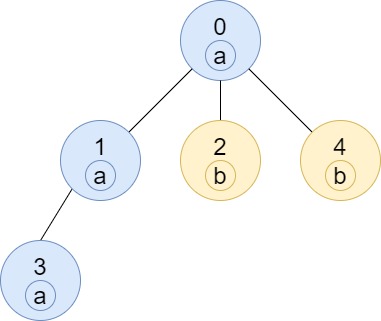
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab" Output: [3,2,1,1,1]
Example 4:
|
1 2 |
<strong>Input:</strong> n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa" <strong>Output:</strong> [1,2,1,1,2,1] |
Example 5:
Input: n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa" Output: [6,5,4,1,3,2,1]
Constraints:
1 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bilabels.length == nlabelsis consisting of only of lower-case English letters.
Solution: Post order traversal + hashtable
For each label, record the count. When visiting a node, we first record the current count of its label as before, and traverse its children, when done, increment the current count, ans[i] = current – before.
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
// Author: Huahua class Solution { public: vector<int> countSubTrees(int n, vector<vector<int>>& edges, string_view labels) { vector<vector<int>> g(n); for (const auto& e : edges) { g[e[0]].push_back(e[1]); g[e[1]].push_back(e[0]); } vector<int> seen(n); vector<int> count(26); vector<int> ans(n); function<void(int)> postOrder = [&](int i) { if (seen[i]++) return; int before = count[labels[i] - 'a']; for (int j : g[i]) postOrder(j); ans[i] = ++count[labels[i] - 'a'] - before; }; postOrder(0); return ans; } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
// Author: Huahua class Solution { private List<List<Integer>> g; private String labels; private int[] ans; private int[] seen; private int[] count; public int[] countSubTrees(int n, int[][] edges, String labels) { this.g = new ArrayList<List<Integer>>(n); this.labels = labels; for (int i = 0; i < n; ++i) this.g.add(new ArrayList<Integer>()); for (int[] e : edges) { this.g.get(e[0]).add(e[1]); this.g.get(e[1]).add(e[0]); } this.ans = new int[n]; this.seen = new int[n]; this.count = new int[26]; this.postOrder(0); return ans; } private void postOrder(int i) { if (this.seen[i]++ > 0) return; int before = this.count[this.labels.charAt(i) - 'a']; for (int j : this.g.get(i)) this.postOrder(j); this.ans[i] = ++this.count[this.labels.charAt(i) - 'a'] - before; } } |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# Author: Huahua class Solution: def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]: g = [[] for _ in range(n)] for u, v in edges: g[u].append(v) g[v].append(u) seen = [False] * n count = [0] * 26 ans = [0] * n def postOrder(i): if seen[i]: return seen[i] = True before = count[ord(labels[i]) - ord('a')] for j in g[i]: postOrder(j) count[ord(labels[i]) - ord('a')] += 1 ans[i] = count[ord(labels[i]) - ord('a')] - before postOrder(0) return ans |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment