花花酱 LeetCode 1530. Number of Good Leaf Nodes Pairs

Given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Return the number of good leaf node pairs in the tree.

Example 1:

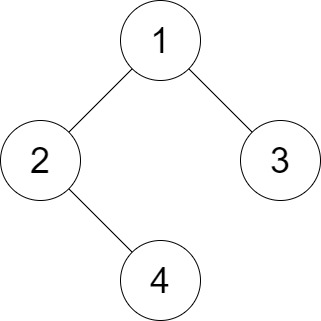
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2:

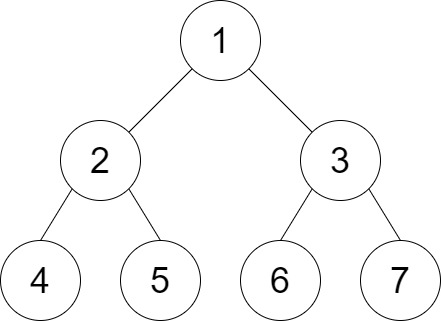
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

Example 3:

Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].

Example 4:

Input: root = [100], distance = 1
Output: 0

Example 5:

Input: root = [1,1,1], distance = 2
Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 2^10].
• Each node’s value is between [1, 100].
• 1 <= distance <= 10

Solution: Brute Force

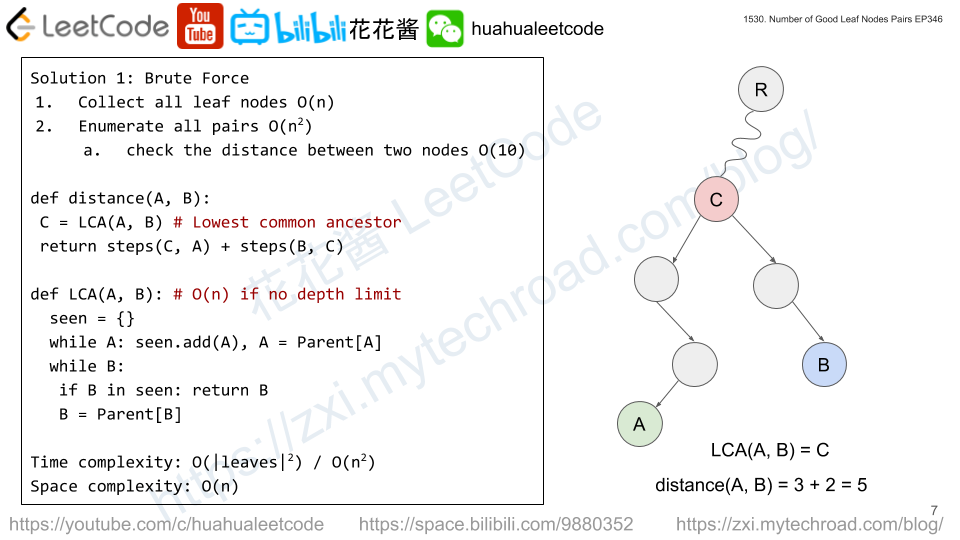
Since n <= 1024, and distance <= 10, we can collect all leaf nodes and try all pairs.

Time complexity: O(|leaves|^2)
Space complexity: O(n)

Solution 2: Post order traversal

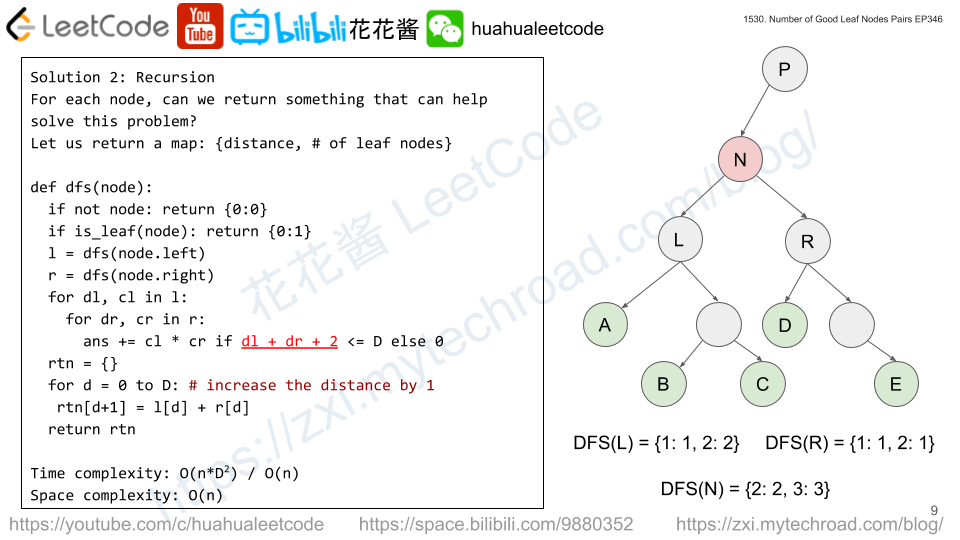
For each node, compute the # of good leaf pair under itself.
1. count the frequency of leaf node at distance 1, 2, …, d for both left and right child.
2. ans += l[i] * r[j] (i + j <= distance) cartesian product
3. increase the distance by 1 for each leaf node when pop
Time complexity: O(n*D^2)
Space complexity: O(n)