花花酱 LeetCode 2096. Step-By-Step Directions From a Binary Tree Node to Another

You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.

Find the shortest path starting from node s and ending at node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

• 'L' means to go from a node to its left child node.
• 'R' means to go from a node to its right child node.
• 'U' means to go from a node to its parent node.

Return the step-by-step directions of the shortest path from node s to node t.

Example 1:

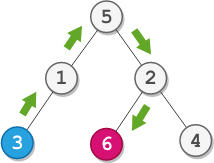
Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

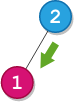
Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• 1 <= startValue, destValue <= n
• startValue != destValue

Solution: Lowest common ancestor

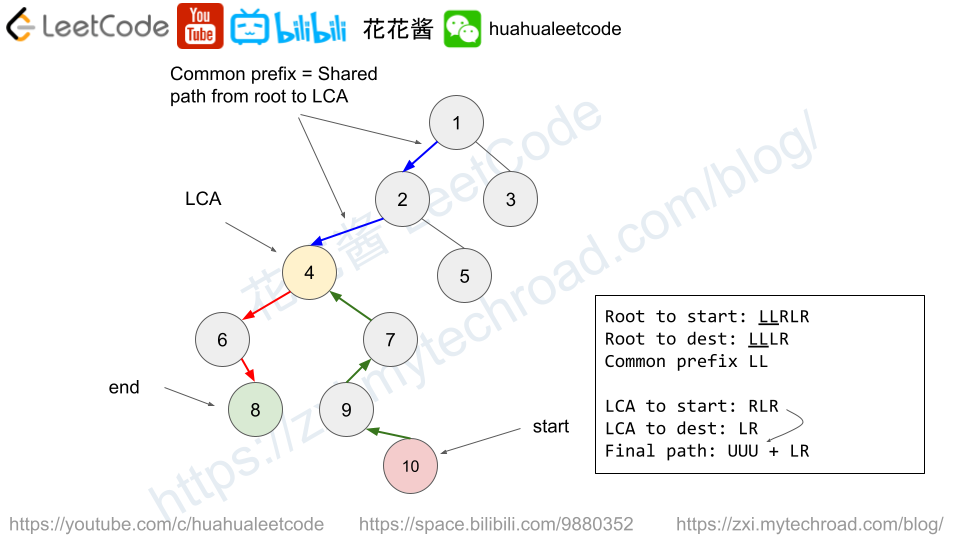
It’s no hard to see that the shortest path is from the start node to the lowest common ancestor (LCA) of (start, end), then to the end node. The key is to find the LCA while finding paths from root to two nodes.

We can use recursion to find/build a path from root to a target node.
The common prefix of these two paths is the path from root to the LCA that we need to remove from the shortest path.
e.g.
root to start “LLRLR”
root to dest “LLLR”
common prefix is “LL”, after removing, it becomes:
LCA to start “RLR”
LCA to dest “LR”
Final path becomes “UUU” + “LR” = “UUULR”

The final step is to replace the L/R with U for the start path since we are moving up and then concatenate with the target path.

Time complexity: O(n)
Space complexity: O(n)