https://leetcode.com/problems/redundant-connection/description/
Problem:
In this problem, a tree is an undirected graph that is connected and has no cycles.
The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, …, N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.
The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.
Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.
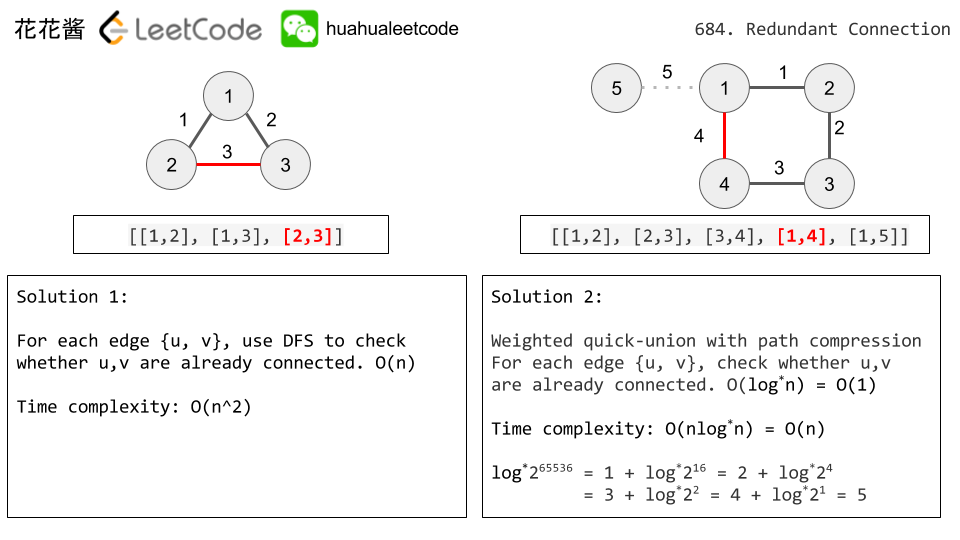
Example 1:
|
1 2 3 4 5 6 |
Input: [[1,2], [1,3], [2,3]] Output: [2,3] Explanation: The given undirected graph will be like this: 1 / \ 2 - 3 |
Example 2:
|
1 2 3 4 5 6 |
Input: [[1,2], [2,3], [3,4], [1,4], [1,5]] Output: [1,4] Explanation: The given undirected graph will be like this: 5 - 1 - 2 | | 4 - 3 |
Note:
- The size of the input 2D-array will be between 3 and 1000.
- Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.
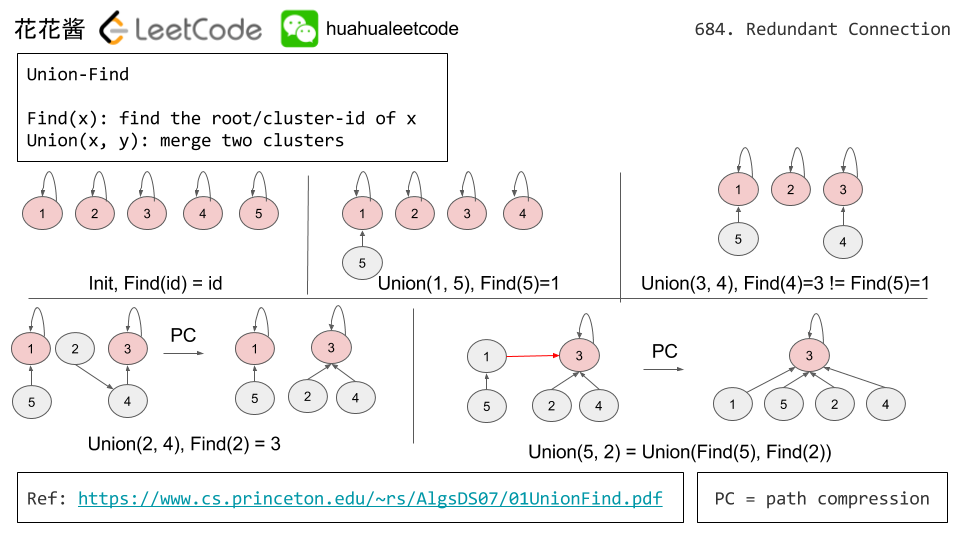
Idea:
DFS / Union-Find
Solutions:
C++ / DFS
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
// Author: Huahua // Time Complexity: O(n^2) // Running Time: 22 ms class Solution { public: vector<int> findRedundantConnection(vector<vector<int>>& edges) { unordered_map<int, vector<int>> graph; for (const auto& edge : edges) { int u = edge[0]; int v = edge[1]; unordered_set<int> visited; if (hasPath(u, v, graph, visited)) return edge; graph[u].push_back(v); graph[v].push_back(u); } return {}; } private: bool hasPath(int curr, int goal, const unordered_map<int, vector<int>>& graph, unordered_set<int>& visited) { if (curr == goal) return true; visited.insert(curr); if (!graph.count(curr) || !graph.count(goal)) return false; for (int next : graph.at(curr)) { if (visited.count(next)) continue; if (hasPath(next, goal, graph, visited)) return true; } return false; } }; |
C++ / Union Find
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
// Author: Huahua // Running time: 6 ms class UnionFindSet { public: UnionFindSet(int n) { ranks_ = vector<int>(n + 1, 0); parents_ = vector<int>(n + 1, 0); for (int i = 0; i < parents_.size(); ++i) parents_[i] = i; } // Merge sets that contains u and v. // Return true if merged, false if u and v are already in one set. bool Union(int u, int v) { int pu = Find(u); int pv = Find(v); if (pu == pv) return false; // Meger low rank tree into high rank tree if (ranks_[pv] > ranks_[pu]) parents_[pu] = pv; else if (ranks_[pu] > ranks_[pv]) parents_[pv] = pu; else { parents_[pv] = pu; ranks_[pv] += 1; } return true; } // Get the root of u. int Find(int u) { // Compress the path during traversal if (u != parents_[u]) parents_[u] = Find(parents_[u]); return parents_[u]; } private: vector<int> parents_; vector<int> ranks_; }; class Solution { public: vector<int> findRedundantConnection(vector<vector<int>>& edges) { UnionFindSet s(edges.size()); for(const auto& edge: edges) if (!s.Union(edge[0], edge[1])) return edge; return {}; } }; |
Java / Union Find
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
// Author: Huahua // Runtime: 6 ms class Solution { class UnionFindSet { private int[] parents_; private int[] ranks_; public UnionFindSet(int n) { parents_ = new int[n + 1]; ranks_ = new int[n + 1]; for (int i = 0; i < parents_.length; ++i) { parents_[i] = i; ranks_[i] = 1; } } public boolean Union(int u, int v) { int pu = Find(u); int pv = Find(v); if (pu == pv) return false; if (ranks_[pv] > ranks_[pu]) parents_[pu] = pv; else if (ranks_[pu] > ranks_[pv]) parents_[pv] = pu; else { parents_[pv] = pu; ranks_[pu] += 1; } return true; } public int Find(int u) { while (parents_[u] != u) { parents_[u] = parents_[parents_[u]]; u = parents_[u]; } return u; } } public int[] findRedundantConnection(int[][] edges) { UnionFindSet s = new UnionFindSet(edges.length); for (int[] edge : edges) if (!s.Union(edge[0], edge[1])) return edge; return null; } } |
Python: Union Find
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
""" Author: Huahua Running Time: 66 ms """ class Solution: def findRedundantConnection(self, edges): p = [0]*(len(edges) + 1) s = [1]*(len(edges) + 1) def find(u): while p[u] != u: p[u] = p[p[u]] u = p[u] return u for u, v in edges: if p[u] == 0: p[u] = u if p[v] == 0: p[v] = v pu, pv = find(u), find(v) if pu == pv: return [u, v] if s[pv] > s[pu]: u, v = v, u p[pv] = pu s[pu] += s[pv] return [] |
Python / Union Find V2
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
""" Author: Huahua Runtime: 59 ms (<92.42%) """ class UnionFindSet: def __init__(self, n): self._parents = [i for i in range(n + 1)] self._ranks = [1 for i in range(n + 1)] def find(self, u): while u != self._parents[u]: self._parents[u] = self._parents[self._parents[u]] u = self._parents[u] return u def union(self, u, v): pu, pv = self.find(u), self.find(v) if pu == pv: return False if self._ranks[pu] < self._ranks[pv]: self._parents[pu] = pv elif self._ranks[pu] > self._ranks[pv]: self._parents[pv] = pu else: self._parents[pv] = pu self._ranks[pu] += 1 return True class Solution: def findRedundantConnection(self, edges): s = UnionFindSet(len(edges)) for edge in edges: if not s.union(edge[0], edge[1]): return edge return None ndSet(len(edges)) for edge in edges: if not s.union(edge[0], edge[1]): return edge return None |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



in the union function, the rank isn’t updated