花花酱 LeetCode 979. Distribute Coins in Binary Tree

Given the root of a binary tree with N nodes, each node in the tree has node.valcoins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another.  (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin.

Example 1:

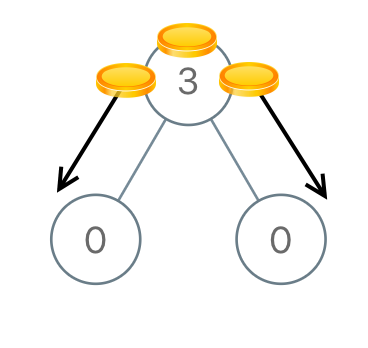
Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

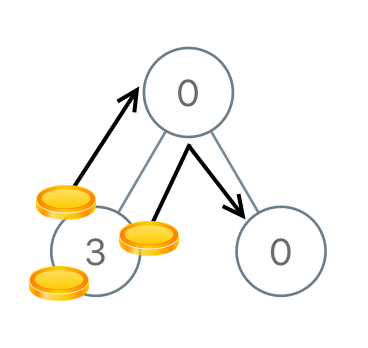
Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves].  Then, we move one coin from the root of the tree to the right child.

Example 3:

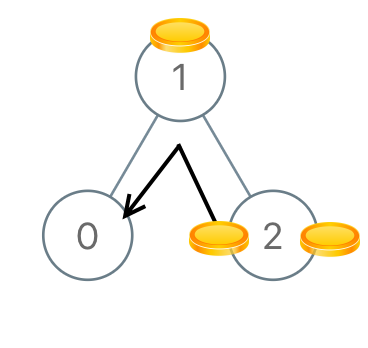
Input: [1,0,2]
Output: 2

Example 4:

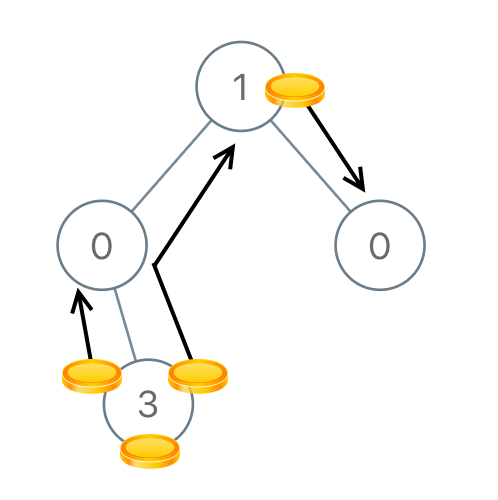
Input: [1,0,0,null,3]
Output: 4

Note:

1. 1<= N <= 100
2. 0 <= node.val <= N

Solution: Recursion

Compute the balance of left/right subtree, ans += abs(balance(left)) + abs(balance(right))
balance(root) = balance(left) + balance(right) + root.val – 1

Time complexity: O(n)
Space complexity: O(n)