You are given two sorted arrays of distinct integers nums1 and nums2.
A validpath is defined as follows:
- Choose array nums1 or nums2 to traverse (from index-0).
- Traverse the current array from left to right.
- If you are reading any value that is present in
nums1andnums2you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
Score is defined as the sum of uniques values in a valid path.
Return the maximum score you can obtain of all possible valid paths.
Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
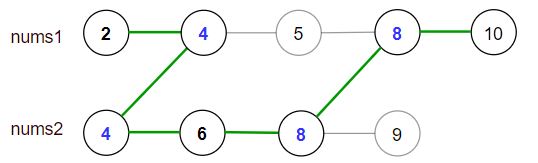
Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9] Output: 30 Explanation: Valid paths: [2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10], (starting from nums1) [4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (starting from nums2) The maximum is obtained with the path in green [2,4,6,8,10].
Example 2:
Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100] Output: 109 Explanation: Maximum sum is obtained with the path [1,3,5,100].
Example 3:
Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10] Output: 40 Explanation: There are no common elements between nums1 and nums2. Maximum sum is obtained with the path [6,7,8,9,10].
Example 4:
Input: nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12] Output: 61
Constraints:
1 <= nums1.length <= 10^51 <= nums2.length <= 10^51 <= nums1[i], nums2[i] <= 10^7nums1andnums2are strictly increasing.
Solution: Two Pointers + DP
Since numbers are strictly increasing, we can always traverse the smaller one using two pointers.
Traversing ([2,4,5,8,10], [4,6,8,10])
will be like [2, 4/4, 5, 6, 8, 10/10]
It two nodes have the same value, we have two choices and pick the larger one, then both move nodes one step forward. Otherwise, the smaller node moves one step forward.
dp1[i] := max path sum ends with nums1[i-1]
dp2[j] := max path sum ends with nums2[j-1]
if nums[i -1] == nums[j – 1]:
dp1[i] = dp2[j] = max(dp[i-1], dp[j-1]) + nums[i -1]
i += 1, j += 1
else if nums[i – 1] < nums[j – 1]:
dp[i] = dp[i-1] + nums[i -1]
i += 1
else if nums[j – 1] < nums[i – 1]:
dp[j] = dp[j-1] + nums[j -1]
j += 1
return max(dp1[-1], dp2[-1])
Time complexity: O(n)
Space complexity: O(n) -> O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class Solution { public: int maxSum(vector<int>& nums1, vector<int>& nums2) { constexpr int kMod = 1e9 + 7; const int n1 = nums1.size(); const int n2 = nums2.size(); vector<long> dp1(n1 + 1); // max path sum ends with nums1[i-1] vector<long> dp2(n2 + 1); // max path sum ends with nums2[j-1] int i = 0; int j = 0; while (i < n1 || j < n2) { if (i < n1 && j < n2 && nums1[i] == nums2[j]) { // Same, two choices, pick the larger one. dp2[j + 1] = dp1[i + 1] = max(dp1[i], dp2[j]) + nums1[i]; ++i; ++j; } else if (i < n1 && (j == n2 || nums1[i] < nums2[j])) { dp1[i + 1] = dp1[i] + nums1[i]; ++i; } else if (j < n2 && (i == n1 || nums2[j] < nums1[i])) { dp2[j + 1] = dp2[j] + nums2[j]; ++j; } } return max(dp1.back(), dp2.back()) % kMod; } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class Solution { public int maxSum(int[] nums1, int[] nums2) { final int kMod = 1_000_000_007; int n1 = nums1.length; int n2 = nums2.length; int i = 0; int j = 0; long a = 0; long b = 0; while (i < n1 || j < n2) { if (i < n1 && j < n2 && nums1[i] == nums2[j]) { a = b = Math.max(a, b) + nums1[i]; ++i; ++j; } else if (i < n1 && (j == n2 || nums1[i] < nums2[j])) { a += nums1[i++]; } else { b += nums2[j++]; } } return (int)(Math.max(a, b) % kMod); } } |
python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class Solution: def maxSum(self, nums1: List[int], nums2: List[int]) -> int: n1, n2 = len(nums1), len(nums2) i, j = 0, 0 a, b = 0, 0 while i < n1 or j < n2: if i < n1 and j < n2 and nums1[i] == nums2[j]: a = b = max(a, b) + nums1[i] i += 1 j += 1 elif i < n1 and (j == n2 or nums1[i] < nums2[j]): a += nums1[i] i += 1 else: b += nums2[j] j += 1 return max(a, b) % (10**9 + 7) |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment