花花酱 LeetCode 1572. Matrix Diagonal Sum

Given a square matrix mat, return the sum of the matrix diagonals.

Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.

Example 1:

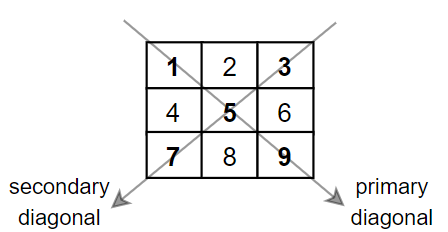
Input: mat = [[1,2,3],
              [4,5,6],
              [7,8,9]]
Output: 25
Explanation: Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat[1][1] = 5 is counted only once.

Example 2:

Input: mat = [[1,1,1,1],
              [1,1,1,1],
              [1,1,1,1],
              [1,1,1,1]]
Output: 8

Example 3:

Input: mat = [[5]]
Output: 5

Constraints:

• n == mat.length == mat[i].length
• 1 <= n <= 100
• 1 <= mat[i][j] <= 100

Solution: Brute Force

Note: if n is odd, be careful not to double count the center one.

Time complexity: O(n)
Space complexity: O(1)