花花酱 LeetCode 1558. Minimum Numbers of Function Calls to Make Target Array

Your task is to form an integer array nums from an initial array of zeros arr that is the same size as nums.

Return the minimum number of function calls to make nums from arr.

The answer is guaranteed to fit in a 32-bit signed integer.

Example 1:

Input: nums = [1,5]
Output: 5
Explanation: Increment by 1 (second element): [0, 0] to get [0, 1] (1 operation).
Double all the elements: [0, 1] -> [0, 2] -> [0, 4] (2 operations).
Increment by 1 (both elements)  [0, 4] -> [1, 4] -> [1, 5] (2 operations).
Total of operations: 1 + 2 + 2 = 5.

Example 2:

Input: nums = [2,2]
Output: 3
Explanation: Increment by 1 (both elements) [0, 0] -> [0, 1] -> [1, 1] (2 operations).
Double all the elements: [1, 1] -> [2, 2] (1 operation).
Total of operations: 2 + 1 = 3.

Example 3:

Input: nums = [4,2,5]
Output: 6
Explanation: (initial)[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5](nums).

Example 4:

Input: nums = [3,2,2,4]
Output: 7

Example 5:

Input: nums = [2,4,8,16]
Output: 8

Constraints:

• 1 <= nums.length <= 10^5
• 0 <= nums[i] <= 10^9

Solution: count 1s

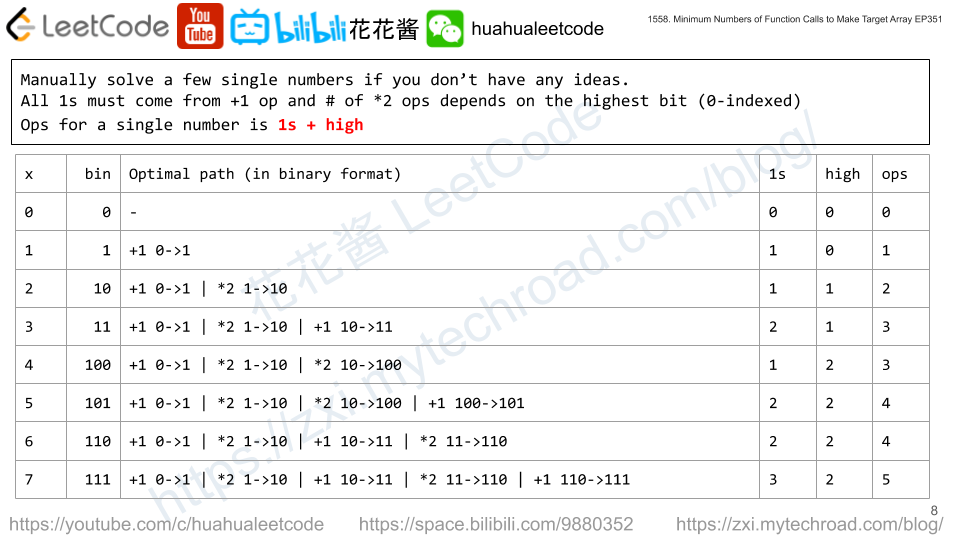
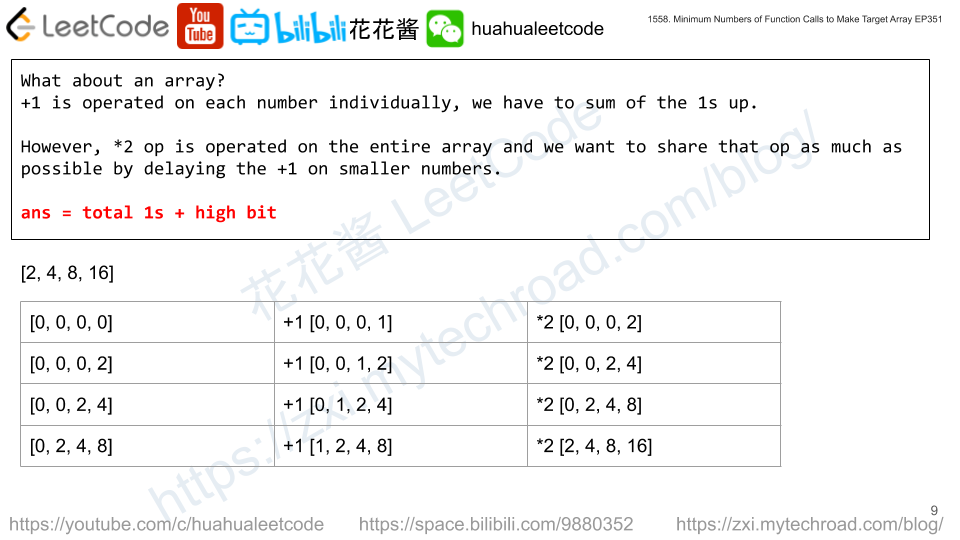
For 5 (101b), we can add 1s for 5 times which of cause isn’t the best way to generate 5, the optimal way is to [+1, *2, +1]. We have to add 1 for each 1 in the binary format. e.g. 11 (1011), we need 3x “+1” op, and 4 “*2” op. Fortunately, the “*2” can be shared/delayed, thus we just need to find the largest number.
e.g. [2,4,8,16]
[0, 0, 0, 0] -> [0, 0, 0, 1] -> [0, 0, 0, 2]
[0, 0, 0, 2] -> [0, 0, 1, 2] -> [0, 0, 2, 4]
[0, 0, 2, 4] -> [0, 1, 2, 4] -> [0, 2, 4, 8]
[0, 2, 4, 8] -> [1, 2, 4, 8] -> [2, 4, 8, 16]
ans = sum{count_1(arr_i)} + high_bit(max(arr_i))

Time complexity: O(n*log(max(arr_i))
Space complexity: O(1)