Posts tagged as “binary”

花花酱 LeetCode 1980. Find Unique Binary String

By zxi on December 31, 2021

Given an array of strings nums containing n unique binary strings each of length n, return a binary string of length n that does not appear in nums. If there are multiple answers, you may return any of them.

Example 1:

Input: nums = ["01","10"]
Output: "11"
Explanation: "11" does not appear in nums. "00" would also be correct.

Example 2:

Input: nums = ["00","01"]
Output: "11"
Explanation: "11" does not appear in nums. "10" would also be correct.

Example 3:

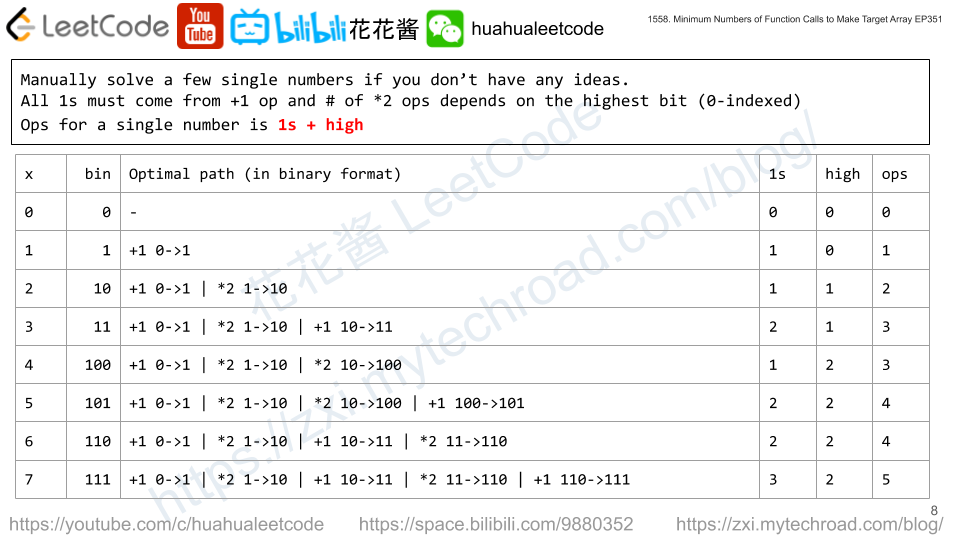
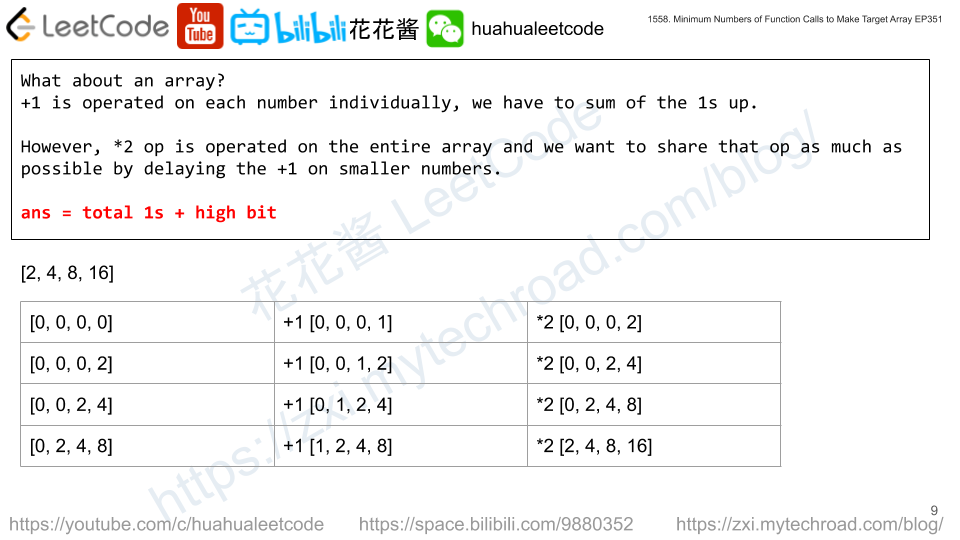
Input: nums = ["111","011","001"]
Output: "101"
Explanation: "101" does not appear in nums. "000", "010", "100", and "110" would also be correct.

Constraints:

n == nums.length
1 <= n <= 16
nums[i].length == n
nums[i] is either '0' or '1'.
All the strings of nums are unique.

Solution 1: Hashtable

We can use bitset to convert between integer and binary string.

Time complexity: O(n²)
Space complexity: O(n²)

C++

// Author: Huahua

class Solution {

public:

string findDifferentBinaryString(vector<string>& nums) {

const int n = nums.size();

unordered_set<int> seen(1 << n);

for (const string& num : nums)

seen.insert(bitset<16>(num).to_ulong());

for (int i = 0; i < 1 << n; ++i)

if (!seen.count(i)) return bitset<16>(i).to_string().substr(16 - n);

return "";

}

};

Solution 2: One bit a time

Let ans[i] = ‘1’ – nums[i][i], s.t. ans is at least one bit different from any strings.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

string findDifferentBinaryString(vector<string>& nums) {

const int n = nums.size();

string ans(n, '0');

for (int i = 0; i < n; ++i)

ans[i] = '1' - nums[i][i] + '0';

return ans;

}

};

花花酱 LeetCode 29. Divide Two Integers

By zxi on November 26, 2021

Given two integers dividend and divisor, divide two integers without using multiplication, division, and mod operator.

The integer division should truncate toward zero, which means losing its fractional part. For example, 8.345 would be truncated to 8, and -2.7335 would be truncated to -2.

Return the quotient after dividing dividend by divisor.

Note: Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−2³¹, 2³¹ − 1]. For this problem, if the quotient is strictly greater than 2³¹ - 1, then return 2³¹ - 1, and if the quotient is strictly less than -2³¹, then return -2³¹.

Example 1:

Input: dividend = 10, divisor = 3
Output: 3
Explanation: 10/3 = 3.33333.. which is truncated to 3.

Example 2:

Input: dividend = 7, divisor = -3
Output: -2
Explanation: 7/-3 = -2.33333.. which is truncated to -2.

Example 3:

Input: dividend = 0, divisor = 1
Output: 0

Example 4:

Input: dividend = 1, divisor = 1
Output: 1

Constraints:

-2³¹ <= dividend, divisor <= 2³¹ - 1
divisor != 0

Solution: Binary / Bit Operation

The answer can be represented in binary format.

a / b = c
a >= b * Σ(d_i*2ⁱ)
c = Σ(d_i*2ⁱ)

e.g. 1: 10 / 3
=> 10 >= 3*(2¹ + 2⁰) = 3 * (2 + 1) = 9
ans = 2¹ + 2⁰ = 3

e.g. 2: 100 / 7
=> 100 >= 7*(2³ + 2²+2¹) = 7 * (8 + 4 + 2) = 7 * 14 = 98
ans = 2³+2²+2¹=8+4+2=14

Time complexity: O(32)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int divide(int A, int B) {

if (B == INT_MIN)

return A == INT_MIN ? 1 : 0;

if (A == INT_MIN) {

if (B == -1) return INT_MAX;

return B > 0 ? divide(A + B, B) - 1 : divide(A - B, B) + 1;

}

int a = abs(A);

int b = abs(B);

int ans = 0;

for (int x = 31; x >= 0; --x)

if (a >> x >= b)

ans += 1 << x, a -= b << x;

return (A > 0) == (B > 0) ? ans : -ans;

}

};

花花酱 LeetCode 1702. Maximum Binary String After Change

By zxi on December 26, 2020

You are given a binary string binary consisting of only 0‘s or 1‘s. You can apply each of the following operations any number of times:

Operation 1: If the number contains the substring "00", you can replace it with "10".
- For example, "00010" -> "10010“
Operation 2: If the number contains the substring "10", you can replace it with "01".
- For example, "00010" -> "00001"

Return the maximum binary string you can obtain after any number of operations. Binary string x is greater than binary string y if x‘s decimal representation is greater than y‘s decimal representation.

Example 1:

Input: binary = "000110"
Output: "111011"
Explanation: A valid transformation sequence can be:
"000110" -> "000101" 
"000101" -> "100101" 
"100101" -> "110101" 
"110101" -> "110011" 
"110011" -> "111011"

Example 2:

Input: binary = "01"
Output: "01"
Explanation: "01" cannot be transformed any further.

Constraints:

1 <= binary.length <= 10⁵
binary consist of '0' and '1'.

Solution: Greedy + Counting

Leading 1s are good, no need to change them.
For the rest of the string
1. Apply operation 2 to make the string into 3 parts, leading 1s, middle 0s and tailing 1s.
e.g. 11010101 => 11001101 => 11001011 => 11000111
2. Apply operation 1 to make flip zeros to ones except the last one.
e.g. 11000111 => 11100111 => 11110111

There will be only one zero (if the input string is not all 1s) is the final largest string, the position of the zero is leading 1s + zeros – 1.

Time complexity: O(n)
Space complexity: O(n)

C++

class Solution {

public:

string maximumBinaryString(string s) {

const int n = s.length();

int l = 0;

int z = 0;

for (char& c : s) {

if (c == '0') {

++z;

} else if (z == 0) { // leading 1s

++l;

}

c = '1';

}

if (l != n) s[l + z - 1] = '0';

return s;

}

};

花花酱 LeetCode 1558. Minimum Numbers of Function Calls to Make Target Array

By zxi on August 22, 2020

Your task is to form an integer array nums from an initial array of zeros arr that is the same size as nums.

Return the minimum number of function calls to make nums from arr.

The answer is guaranteed to fit in a 32-bit signed integer.

Example 1:

Input: nums = [1,5]
Output: 5
Explanation: Increment by 1 (second element): [0, 0] to get [0, 1] (1 operation).
Double all the elements: [0, 1] -> [0, 2] -> [0, 4] (2 operations).
Increment by 1 (both elements)  [0, 4] -> [1, 4] -> [1, 5] (2 operations).
Total of operations: 1 + 2 + 2 = 5.

Example 2:

Input: nums = [2,2]
Output: 3
Explanation: Increment by 1 (both elements) [0, 0] -> [0, 1] -> [1, 1] (2 operations).
Double all the elements: [1, 1] -> [2, 2] (1 operation).
Total of operations: 2 + 1 = 3.

Example 3:

Input: nums = [4,2,5]
Output: 6
Explanation: (initial)[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5](nums).

Example 4:

Input: nums = [3,2,2,4]
Output: 7

Example 5:

Input: nums = [2,4,8,16]
Output: 8

Constraints:

1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9

Solution: count 1s

For 5 (101b), we can add 1s for 5 times which of cause isn’t the best way to generate 5, the optimal way is to [+1, *2, +1]. We have to add 1 for each 1 in the binary format. e.g. 11 (1011), we need 3x “+1” op, and 4 “*2” op. Fortunately, the “*2” can be shared/delayed, thus we just need to find the largest number.
e.g. [2,4,8,16]
[0, 0, 0, 0] -> [0, 0, 0, 1] -> [0, 0, 0, 2]
[0, 0, 0, 2] -> [0, 0, 1, 2] -> [0, 0, 2, 4]
[0, 0, 2, 4] -> [0, 1, 2, 4] -> [0, 2, 4, 8]
[0, 2, 4, 8] -> [1, 2, 4, 8] -> [2, 4, 8, 16]
ans = sum{count_1(arr_i)} + high_bit(max(arr_i))

Time complexity: O(n*log(max(arr_i))
Space complexity: O(1)

C++

class Solution {

public:

int minOperations(vector<int>& nums) {

int ans = 0;

int high = 0;

for (int x : nums) {

high = max(high, 31 - __builtin_clz(x | 1));

ans += std::bitset<32>(x).count();

}

return ans + high;

}

};

Java

class Solution {

public int minOperations(int[] nums) {

int ans = 0;

int high = 0;

for (int x : nums) {

int l = -1;

while (x != 0) {

ans += x & 1;

x >>= 1;

++l;

}

high = Math.max(high, l);

}

return ans + high;

}

Python3

class Solution:

def minOperations(self, nums: List[int]) -> int:

return sum(bin(x).count('1') for x in nums) + len(bin(max(nums))) - 3

花花酱 LeetCode 1261. Find Elements in a Contaminated Binary Tree

By zxi on November 26, 2019

Given a binary tree with the following rules:

root.val == 0
If treeNode.val == x and treeNode.left != null, then treeNode.left.val == 2 * x + 1
If treeNode.val == x and treeNode.right != null, then treeNode.right.val == 2 * x + 2

Now the binary tree is contaminated, which means all treeNode.val have been changed to -1.

You need to first recover the binary tree and then implement the FindElements class:

FindElements(TreeNode* root) Initializes the object with a contamined binary tree, you need to recover it first.
bool find(int target) Return if the target value exists in the recovered binary tree.

Example 1:

Input
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
Output

[null,false,true]

Explanation FindElements findElements = new FindElements([-1,null,-1]); findElements.find(1); // return False findElements.find(2); // return True

Example 2:

Input
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
Output

[null,true,true,false]

Explanation FindElements findElements = new FindElements([-1,-1,-1,-1,-1]); findElements.find(1); // return True findElements.find(3); // return True findElements.find(5); // return False

Example 3:

Input
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
Output

[null,true,false,false,true]

Explanation FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]); findElements.find(2); // return True findElements.find(3); // return False findElements.find(4); // return False findElements.find(5); // return True

Constraints:

TreeNode.val == -1
The height of the binary tree is less than or equal to 20
The total number of nodes is between [1, 10^4]
Total calls of find() is between [1, 10^4]
0 <= target <= 10^6

Solutoin 1: Recursion and HashSet

Time complexity: Recover O(n), find O(1)
Space complexity: O(n)

C++

// Author: Huahua

class FindElements {

public:

FindElements(TreeNode* root) {

recover(root, 0);

}

bool find(int target) {

return s_.count(target);

}

private:

unordered_set<int> s_;

void recover(TreeNode* root, int val) {

if (!root) return;

root->val = val;

s_.insert(val);

recover(root->left, val * 2 + 1);

recover(root->right, val * 2 + 2);

}

};

Solution 2: Recursion and Binary format

The binary format of t = (target + 1) (from high bit to low bit, e.g. in reverse order) decides where to go at each node.
t % 2 == 1, go right, otherwise go left
t = t / 2 or t >>= 1

e.g. target = 13, t = 13 + 1 = 14

t = 14, t % 1 = 0, t / 2 = 7, left

t = 7, t % 1 = 1, t / 2 = 3, right

t = 3, t % 1 = 1, t / 2 = 1, right

13 => right, right, left

Time complexity: Recover O(n), find O(log|target|)
Space complexity: O(1)

C++

// Author: Huahua

class FindElements {

public:

FindElements(TreeNode* root): root_(root) {

recover(root, 0);

}

bool find(int target) {

++target;

stack<bool> right;

while (target != 1) {

right.push(target & 1);

target >>= 1;

}

TreeNode* node = root_;

while (!right.empty() && node) {

node = right.top() ? node->right : node->left;

right.pop();

}

return node;

}

private:

TreeNode* root_;

void recover(TreeNode* root, int val) {

if (!root) return;

root->val = val;

recover(root->left, val * 2 + 1);

recover(root->right, val * 2 + 2);

}

};