Posts published in “Data Structure”

花花酱 LeetCode 1825. Finding MK Average

By zxi on April 13, 2021

You are given two integers, m and k, and a stream of integers. You are tasked to implement a data structure that calculates the MKAverage for the stream.

The MKAverage can be calculated using these steps:

If the number of the elements in the stream is less than m you should consider the MKAverage to be -1. Otherwise, copy the last m elements of the stream to a separate container.
Remove the smallest k elements and the largest k elements from the container.
Calculate the average value for the rest of the elements rounded down to the nearest integer.

Implement the MKAverage class:

MKAverage(int m, int k) Initializes the MKAverage object with an empty stream and the two integers m and k.
void addElement(int num) Inserts a new element num into the stream.
int calculateMKAverage() Calculates and returns the MKAverage for the current stream rounded down to the nearest integer.

Example 1:

Input
["MKAverage", "addElement", "addElement", "calculateMKAverage", "addElement", "calculateMKAverage", "addElement", "addElement", "addElement", "calculateMKAverage"]
[[3, 1], [3], [1], [], [10], [], [5], [5], [5], []]
Output
[null, null, null, -1, null, 3, null, null, null, 5]
Explanation MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5

Constraints:

3 <= m <= 10⁵
1 <= k*2 < m
1 <= num <= 10⁵
At most 10⁵ calls will be made to addElement and calculateMKAverage.

**Solution 1: Multiset * 3**

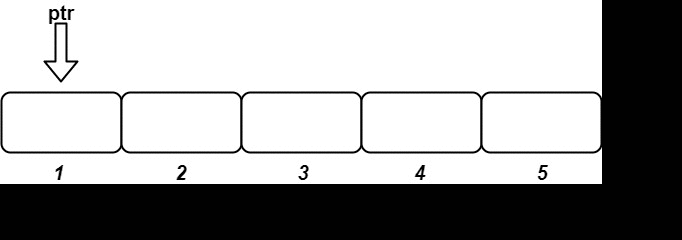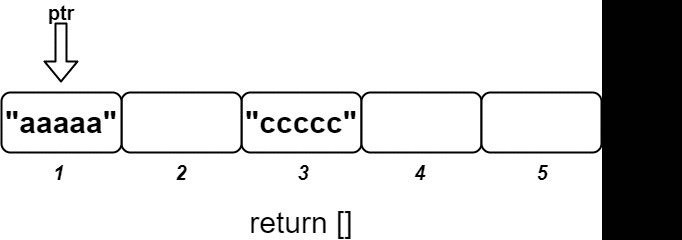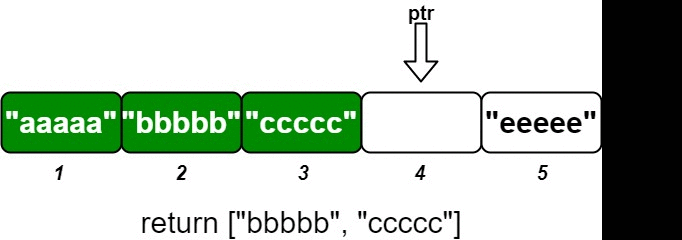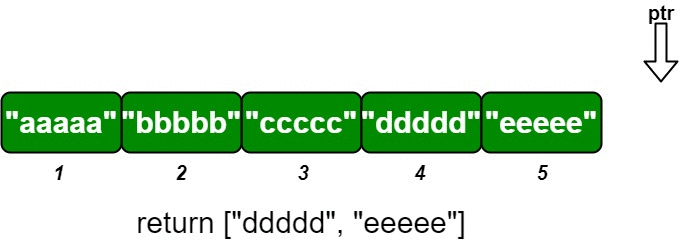
Use three multiset to track the left part (smallest k elements), right part (largest k elements) and mid (middle part of m – 2*k elements).

Time complexity: addElememt: O(logn), average: O(1)
Space complexity: O(n)

C++

class MKAverage {

public:

MKAverage(int m, int k):

sum(0), m(m), k(k), n(m - 2*k) {}

void addElement(int num) {

if (q.size() == m) {

remove(q.front());

q.pop();

}

q.push(num);

add(num);

}

int calculateMKAverage() {

return (q.size() < m) ? -1 : sum / n;

}

private:

void add(int x) {

left.insert(x);

if (left.size() > k) {

auto it = prev(end(left));

sum += *it;

mid.insert(*it);

left.erase(it);

}

if (mid.size() > n) {

auto it = prev(end(mid));

sum -= *it;

right.insert(*it);

mid.erase(it);

}

void remove(int x) {

if (x <= *rbegin(left)) {

left.erase(left.find(x));

} else if (x <= *rbegin(mid)) {

sum -= x;

mid.erase(mid.find(x));

} else {

right.erase(right.find(x));

}

if (left.size() < k) {

auto it = begin(mid);

sum -= *it;

left.insert(*it);

mid.erase(it);

}

if (mid.size() < n) {

auto it = begin(right);

sum += *it;

mid.insert(*it);

right.erase(it);

}

queue<int> q;

multiset<int> left, mid, right;

long sum;

const int m;

const int k;

const int n;

};

花花酱 LeetCode 1656. Design an Ordered Stream

By zxi on November 14, 2020

There are n (id, value) pairs, where id is an integer between 1 and n and value is a string. No two pairs have the same id.

Design a stream that takes the n pairs in an arbitrary order, and returns the values over several calls in increasing order of their ids.

Implement the OrderedStream class:

OrderedStream(int n) Constructs the stream to take n values and sets a current ptr to 1.
String[] insert(int id, String value) Stores the new (id, value) pair in the stream. After storing the pair:
- If the stream has stored a pair with id = ptr, then find the longest contiguous incrementing sequence of ids starting with id = ptr and return a list of the values associated with those ids in order. Then, update ptr to the last id + 1.
- Otherwise, return an empty list.

Example:

Input
["OrderedStream", "insert", "insert", "insert", "insert", "insert"]
[[5], [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"], [5, "eeeee"], [4, "ddddd"]]
Output
[null, [], ["aaaaa"], ["bbbbb", "ccccc"], [], ["ddddd", "eeeee"]]
Explanation
OrderedStream os= new OrderedStream(5);
os.insert(3, "ccccc"); // Inserts (3, "ccccc"), returns [].
os.insert(1, "aaaaa"); // Inserts (1, "aaaaa"), returns ["aaaaa"].
os.insert(2, "bbbbb"); // Inserts (2, "bbbbb"), returns ["bbbbb", "ccccc"].
os.insert(5, "eeeee"); // Inserts (5, "eeeee"), returns [].
os.insert(4, "ddddd"); // Inserts (4, "ddddd"), returns ["ddddd", "eeeee"].

Solution: Straight Forward

Time complexity: O(n) in total
Space complexity: O(n)

C++

// Author: Huahua

class OrderedStream {

public:

OrderedStream(int n): data_(n + 1) {}

vector<string> insert(int id, string value) {

data_[id] = value;

vector<string> ans;

if (ptr_ == id)

while (ptr_ < data_.size() && !data_[ptr_].empty())

ans.push_back(data_[ptr_++]);

return ans;

}

private:

int ptr_ = 1;

vector<string> data_;

};

Python3

# Author: Huahua

class OrderedStream:

def __init__(self, n: int):

self.data = [None] * (n + 1)

self.ptr = 1

def insert(self, id: int, value: str) -> List[str]:

self.data[id] = value

if id == self.ptr:

while self.ptr < len(self.data) and self.data[self.ptr]:

self.ptr += 1

return self.data[id:self.ptr]

return []

花花酱 LeetCode 1146. Snapshot Array

By zxi on August 4, 2019

Implement a SnapshotArray that supports the following interface:

SnapshotArray(int length) initializes an array-like data structure with the given length. Initially, each element equals 0.
void set(index, val) sets the element at the given index to be equal to val.
int snap() takes a snapshot of the array and returns the snap_id: the total number of times we called snap() minus 1.
int get(index, snap_id) returns the value at the given index, at the time we took the snapshot with the given snap_id

Example 1:

Input: ["SnapshotArray","set","snap","set","get"]
[[3],[0,5],[],[0,6],[0,0]]
Output: [null,null,0,null,5]
Explanation: 
SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3
snapshotArr.set(0,5);  // Set array[0] = 5
snapshotArr.snap();  // Take a snapshot, return snap_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0);  // Get the value of array[0] with snap_id = 0, return 5

Constraints:

1 <= length <= 50000
At most 50000 calls will be made to set, snap, and get.
0 <= index < length
0 <= snap_id < (the total number of times we call snap())
0 <= val <= 10^9

Solution: map + upper_bound

Use a vector to store maps, one map per element.
The map stores {snap_id -> val}, use upper_bound to find the first version > snap_id and use previous version’s value.

Time complexity:
Set: O(log|snap_id|)
Get: O(log|snap_id|)
Snap: O(1)
Space complexity: O(length + set_calls)

C++

// Author: Huahua

class SnapshotArray {

public:

SnapshotArray(int length): id_(0), vals_(length) {}

void set(int index, int val) {

vals_[index][id_] = val;

}

int snap() { return id_++; }

int get(int index, int snap_id) const {

auto it = vals_[index].upper_bound(snap_id);

if (it == begin(vals_[index])) return 0;

return prev(it)->second;

}

private:

int id_;

vector<map<int, int>> vals_;

};

花花酱 LeetCode 641. Design Circular Deque

By zxi on July 14, 2018

Problem

Design your implementation of the circular double-ended queue (deque).
Your implementation should support following operations:

MyCircularDeque(k): Constructor, set the size of the deque to be k.
insertFront(): Adds an item at the front of Deque. Return true if the operation is successful.
insertLast(): Adds an item at the rear of Deque. Return true if the operation is successful.
deleteFront(): Deletes an item from the front of Deque. Return true if the operation is successful.
deleteLast(): Deletes an item from the rear of Deque. Return true if the operation is successful.
getFront(): Gets the front item from the Deque. If the deque is empty, return -1.
getRear(): Gets the last item from Deque. If the deque is empty, return -1.
isEmpty(): Checks whether Deque is empty or not.
isFull(): Checks whether Deque is full or not.

Example:

MyCircularDeque circularDeque = new MycircularDeque(3); // set the size to be 3
circularDeque.insertLast(1);			// return true
circularDeque.insertLast(2);			// return true
circularDeque.insertFront(3);			// return true
circularDeque.insertFront(4);			// return false, the queue is full
circularDeque.getRear();  				// return 32
circularDeque.isFull();				// return true
circularDeque.deleteLast();			// return true
circularDeque.insertFront(4);			// return true
circularDeque.getFront();				// return 4

Note:

All values will be in the range of [1, 1000].
The number of operations will be in the range of [1, 1000].
Please do not use the built-in Deque library.

Solution

Using head and tail to pointer to the head and the tail in the circular buffer.

// Author: Huahua

// Running time: 20 ms

class MyCircularDeque {

public:

/** Initialize your data structure here. Set the size of the deque to be k. */

MyCircularDeque(int k): k_(k), q_(k), head_(1), tail_(-1), size_(0) {}

/** Adds an item at the front of Deque. Return true if the operation is successful. */

bool insertFront(int value) {

if (isFull()) return false;

head_ = (head_ - 1 + k_) % k_;

q_[head_] = value;

if (size_ == 0) tail_ = head_;

++size_;

return true;

}

/** Adds an item at the rear of Deque. Return true if the operation is successful. */

bool insertLast(int value) {

if (isFull()) return false;

tail_ = (tail_ + 1 + k_) % k_;

q_[tail_] = value;

if (size_ == 0) head_ = tail_;

++size_;

return true;

}

/** Deletes an item from the front of Deque. Return true if the operation is successful. */

bool deleteFront() {

if (isEmpty()) return false;

head_ = (head_ + 1 + k_) % k_;

--size_;

return true;

}

/** Deletes an item from the rear of Deque. Return true if the operation is successful. */

bool deleteLast() {

if (isEmpty()) return false;

tail_ = (tail_ - 1 + k_) % k_;

--size_;

return true;

}

/** Get the front item from the deque. */

int getFront() {

if (isEmpty()) return -1;

return q_[head_];

}

/** Get the last item from the deque. */

int getRear() {

if (isEmpty()) return -1;

return q_[tail_];

}

/** Checks whether the circular deque is empty or not. */

bool isEmpty() {

return size_ == 0;

}

/** Checks whether the circular deque is full or not. */

bool isFull() {

return size_ == k_;

}

private:

const int k_;

int head_;

int tail_;

int size_;

vector<int> q_;

};

Problem

题目大意：设计一种数据结构，支持inc/dec/getmaxkey/getminkey操作，必须都在O(1)时间内完成。

https://leetcode.com/problems/all-oone-data-structure/description/

Implement a data structure supporting the following operations:

Inc(Key) – Inserts a new key with value 1. Or increments an existing key by 1. Key is guaranteed to be a non-empty string.
Dec(Key) – If Key’s value is 1, remove it from the data structure. Otherwise decrements an existing key by 1. If the key does not exist, this function does nothing. Key is guaranteed to be a non-empty string.
GetMaxKey() – Returns one of the keys with maximal value. If no element exists, return an empty string "".
GetMinKey() – Returns one of the keys with minimal value. If no element exists, return an empty string "".

Challenge: Perform all these in O(1) time complexity.

Solution

Time complexity: O(1)

Space complexity: O(n), n = # of unique keys

// Author: Huahua

// Running time: 32 ms

class AllOne {

public:

/** Initialize your data structure here. */

AllOne() {}

/** Inserts a new key <Key> with value 1. Or increments an existing key by 1. */

void inc(string key) {

auto it = m_.find(key);

if (it == m_.end()) {

if (l_.empty() || l_.front().value != 1)

l_.push_front({1, {key}});

else

l_.front().keys.insert(key);

m_[key] = l_.begin();

return;

}

auto lit = it->second;

auto nit = next(lit);

if (nit == l_.end() || nit->value != lit->value + 1)

nit = l_.insert(nit, {lit->value + 1, {}});

nit->keys.insert(key);

m_[key] = nit;

remove(lit, key);

}

/** Decrements an existing key by 1. If Key's value is 1, remove it from the data structure. */

void dec(string key) {

auto it = m_.find(key);

if (it == m_.end()) return;

auto lit = it->second;

if (lit->value > 1) {

auto pit = prev(lit);

if (lit == l_.begin() || pit->value != lit->value - 1)

pit = l_.insert(lit, {lit->value - 1, {}});

pit->keys.insert(key);

m_[key] = pit;

} else {

// value == 1, remove from the data structure

m_.erase(key);

}

remove(lit, key);

}

/** Returns one of the keys with maximal value. */

string getMaxKey() {

return l_.empty() ? "" : *l_.back().keys.cbegin();

}

/** Returns one of the keys with Minimal value. */

string getMinKey() {

return l_.empty() ? "" : *l_.front().keys.cbegin();

}

private:

struct Node {

int value;

unordered_set<string> keys;

};

list<Node> l_;

unordered_map<string, list<Node>::iterator> m_;

// Remove from old node.

void remove(list<Node>::iterator it, const string& key) {

it->keys.erase(key);

if (it->keys.empty())

l_.erase(it);

}

};

Posts published in “Data Structure”

花花酱 LeetCode 1825. Finding MK Average

Solution 1: Multiset * 3

C++

花花酱 LeetCode 1656. Design an Ordered Stream

Solution: Straight Forward

C++

Python3

花花酱 LeetCode 1146. Snapshot Array

Solution: map + upper_bound

C++

花花酱 LeetCode 641. Design Circular Deque

Problem

Solution

Related Problems

花花酱 LeetCode 432. All O`one Data Structure

Problem

Solution

Related Problems

**Solution 1: Multiset * 3**